

青海省西宁市三年(2020-2022)中考数学真题分类汇编-选择题
展开青海省西宁市三年(2020-2022)中考数学真题分类汇编-选择题
一.正数和负数(共1小题)
1.(2022•西宁)下列各数是负数的是( )
A.0 B. C.﹣(﹣5) D.
二.相反数(共1小题)
2.(2020•西宁)3的相反数是( )
A. B. C.3 D.﹣3
三.有理数的加法(共1小题)
3.(2021•西宁)中国人最先使用负数,魏晋时期的数学家刘徽在其著作《九章算术注》中,用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(红色为正,黑色为负).如图1表示的是(+2)+(﹣2),根据这种表示法,可推算出图2所表示的算式是( )
A.(+3)+(+6) B.(+3)+(﹣6) C.(﹣3)+(+6) D.(﹣3)+(﹣6)
四.实数的性质(共1小题)
4.(2021•西宁)﹣的相反数是( )
A. B.﹣ C. D.﹣
五.同底数幂的除法(共1小题)
5.(2020•西宁)下列计算正确的是( )
A.(﹣a3)2=﹣a6 B.a3•a2=a6 C.(2a)2=2a2 D.a3÷a2=a
六.完全平方公式(共1小题)
6.(2022•西宁)下列运算正确的是( )
A.a2+a4=a6 B.(a﹣b)2=a2﹣b2
C.(a2b)3=a6b3 D.a6÷a6=a
七.最简二次根式(共1小题)
7.(2020•西宁)下列二次根式中,最简二次根式的是( )
A. B. C. D.
八.由实际问题抽象出一元一次方程(共1小题)
8.(2022•西宁)在数学活动课上,兴趣小组的同学用一根质地均匀的轻质木杆和若干个钩码做实验.如图所示,在轻质木杆O处用一根细线悬挂,左端A处挂一重物,右端B处挂钩码,每个钩码质量是50g.若OA=20cm,OB=40cm,挂3个钩码可使轻质木杆水平位置平衡.设重物的质量为xg,根据题意列方程得( )
A.20x=40×50×3 B.40x=20×50×3
C.3×20x=40×50 D.3×40x=20×50
九.根的判别式(共1小题)
9.(2022•西宁)关于x的一元二次方程2x2+x﹣k=0没有实数根,则k的取值范围是( )
A.k<﹣ B.k≤﹣ C.k>﹣ D.k≥﹣
一十.由实际问题抽象出一元二次方程(共1小题)
10.(2021•西宁)某市严格落实国家节水政策,2018年用水总量为6.5亿立方米,2020年用水总量为5.265亿立方米.设该市用水总量的年平均降低率是x,那么x满足的方程是( )
A.6.5(1﹣x)2=5.265 B.6.5(1+x)2=5.265
C.5.265(1﹣x)2=6.5 D.5.265(1+x)2=6.5
一十一.函数的图象(共1小题)
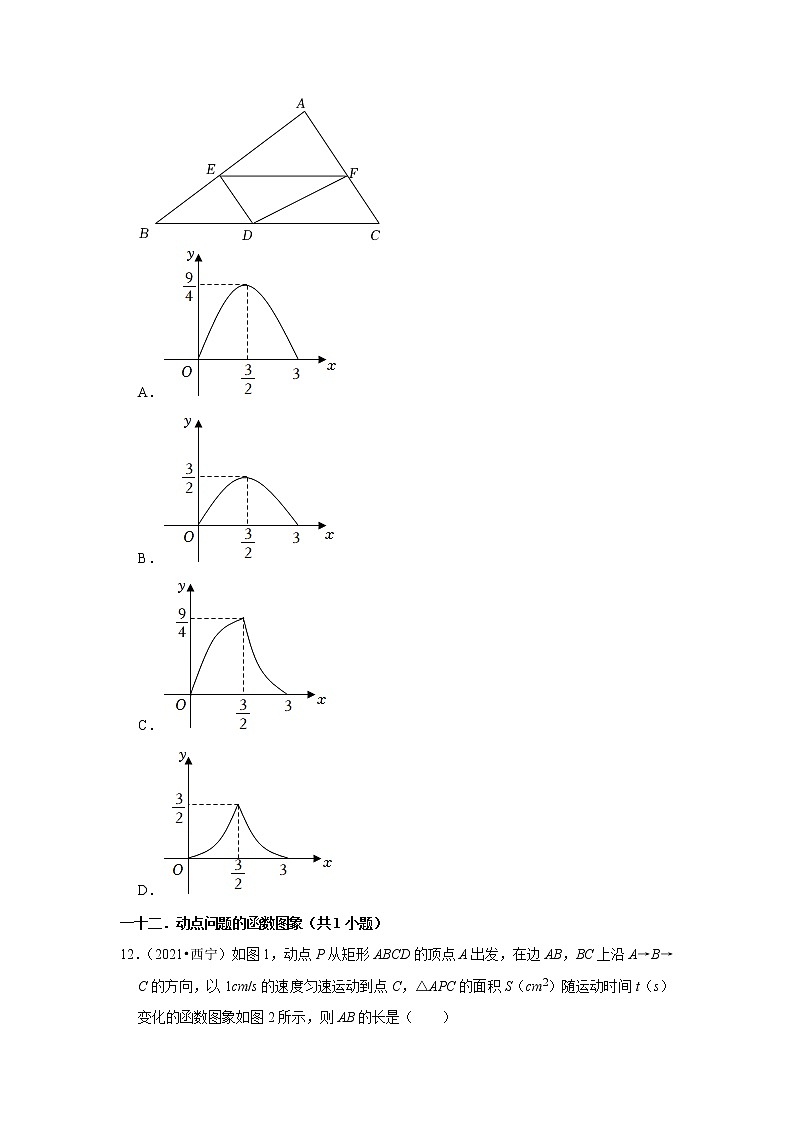
11.(2022•西宁)如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
一十二.动点问题的函数图象(共1小题)
12.(2021•西宁)如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,△APC的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
A.cm B.3cm C.4cm D.6cm
一十三.一次函数的应用(共1小题)
13.(2020•西宁)全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( )
A.60米/分,40米/分 B.80米/分,60米/分
C.80米/分,40米/分 D.120米/分,80米/分
一十四.二次函数的图象(共1小题)
14.(2020•西宁)函数y=ax2+1和y=ax+a(a为常数,且a≠0),在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
一十五.三角形三边关系(共1小题)
15.(2022•西宁)若长度是4,6,a的三条线段能组成一个三角形,则a的值可以是( )
A.2 B.5 C.10 D.11
一十六.全等三角形的判定与性质(共1小题)
16.(2022•西宁)如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( )
A.△AOB是等边三角形 B.PE=PF
C.△PAE≌△PBF D.四边形OAPB是菱形
一十七.切线长定理(共1小题)
17.(2020•西宁)如图,PA,PB与⊙O分别相切于点A,B,PA=2,∠P=60°,则AB=( )
A. B.2 C. D.3
一十八.三角形的内切圆与内心(共1小题)
18.(2021•西宁)如图,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,连接OE,OF,∠C=90°,AC=6,BC=8,则阴影部分的面积为( )
A. B. C.4﹣π D.
一十九.命题与定理(共1小题)
19.(2021•西宁)下列命题是真命题的是( )
A.同位角相等
B.是分式
C.数据6,3,10的中位数是3
D.第七次全国人口普查是全面调查
二十.翻折变换(折叠问题)(共1小题)
20.(2020•西宁)如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=BN,AD=3AM,E为BC边上一动点,连接DE,将△DCE沿DE所在直线折叠得到△DC′E,当C′点恰好落在线段MN上时,CE的长为( )
A.或2 B. C.或2 D.
二十一.中心对称图形(共1小题)
21.(2021•西宁)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.三角形 B.等边三角形 C.平行四边形 D.菱形
二十二.简单几何体的三视图(共1小题)
22.(2020•西宁)在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称之为“阳马”(如图).“阳马”的俯视图是( )
A. B.
C. D.
二十三.由三视图判断几何体(共1小题)
23.(2021•西宁)某几何体的三视图如图所示,则此几何体是( )
A.圆锥 B.长方体 C.圆柱 D.四棱柱
二十四.众数(共1小题)
24.(2022•西宁)家务劳动是劳动教育的一个重要方面,教育部基础教育司发布通知要求家长引导孩子力所能及地做一些家务劳动.某校为了解七年级学生平均每周在家的劳动时间,随机抽取了部分七年级学生进行调查,根据调查结果,绘制了如下频数分布表:
组别
一
二
三
四
劳动时间x/h
0≤x<1
1≤x<2
2≤x<3
x≥3
频数
10
20
12
8
根据表中的信息,下列说法正确的是( )
A.本次调查的样本容量是50人
B.本次调查七年级学生平均每周在家劳动时间的中位数落在二组
C.本次调查七年级学生平均每周在家劳动时间的众数落在四组
D.若七年级共有500名学生,估计平均每周在家劳动时间在四组的学生大约有100人
青海省西宁市三年(2020-2022)中考数学真题分类汇编-选择题
参考答案与试题解析
一.正数和负数(共1小题)
1.(2022•西宁)下列各数是负数的是( )
A.0 B. C.﹣(﹣5) D.
【解答】解:A.0既不是正数也不是负数,故A不符合题意;
B.>0,故B不符合题意;
C.﹣(﹣5)=5,5>0,故C不符合题意;
D.﹣<0,故D符合题意;
故选:D.
二.相反数(共1小题)
2.(2020•西宁)3的相反数是( )
A. B. C.3 D.﹣3
【解答】解:3的相反数是﹣3,
故选:D.
三.有理数的加法(共1小题)
3.(2021•西宁)中国人最先使用负数,魏晋时期的数学家刘徽在其著作《九章算术注》中,用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(红色为正,黑色为负).如图1表示的是(+2)+(﹣2),根据这种表示法,可推算出图2所表示的算式是( )
A.(+3)+(+6) B.(+3)+(﹣6) C.(﹣3)+(+6) D.(﹣3)+(﹣6)
【解答】解:由题意可知:(+3)+(﹣6),
故选:B.
四.实数的性质(共1小题)
4.(2021•西宁)﹣的相反数是( )
A. B.﹣ C. D.﹣
【解答】解:﹣的相反数是.
故选:A.
五.同底数幂的除法(共1小题)
5.(2020•西宁)下列计算正确的是( )
A.(﹣a3)2=﹣a6 B.a3•a2=a6 C.(2a)2=2a2 D.a3÷a2=a
【解答】解:A.结果是a6,故本选项不符合题意;
B.结果是a5,故本选项不符合题意;
C.结果是4a2,故本选项不符合题意;
D.结果是a,故本选项符合题意;
故选:D.
六.完全平方公式(共1小题)
6.(2022•西宁)下列运算正确的是( )
A.a2+a4=a6 B.(a﹣b)2=a2﹣b2
C.(a2b)3=a6b3 D.a6÷a6=a
【解答】解:∵a2,a4不是同类项,不能合并,
∴A不合题意.
∵(a﹣b)2=a2﹣2ab+b2,
∴B不合题意.
∵(a2b)3=a6b3,
∴C符合题意.
∵a6÷a6=a0=1,
∴D不合题意.
故选:C.
七.最简二次根式(共1小题)
7.(2020•西宁)下列二次根式中,最简二次根式的是( )
A. B. C. D.
【解答】解:A、中被开方数是分数,故不是最简二次根式;
B、中被开方数是分数,故不是最简二次根式;
C、中被开方数不含分母,不含能开得尽方的因数或因式,故是最简二次根式;
D、中含能开得尽方的因数,故不是最简二次根式;
故选:C.
八.由实际问题抽象出一元一次方程(共1小题)
8.(2022•西宁)在数学活动课上,兴趣小组的同学用一根质地均匀的轻质木杆和若干个钩码做实验.如图所示,在轻质木杆O处用一根细线悬挂,左端A处挂一重物,右端B处挂钩码,每个钩码质量是50g.若OA=20cm,OB=40cm,挂3个钩码可使轻质木杆水平位置平衡.设重物的质量为xg,根据题意列方程得( )
A.20x=40×50×3 B.40x=20×50×3
C.3×20x=40×50 D.3×40x=20×50
【解答】解:依题意得:20x=40×50×3.
故选:A.
九.根的判别式(共1小题)
9.(2022•西宁)关于x的一元二次方程2x2+x﹣k=0没有实数根,则k的取值范围是( )
A.k<﹣ B.k≤﹣ C.k>﹣ D.k≥﹣
【解答】解:∵关于x的一元二次方程2x2+x﹣k=0没有实数根,
∴Δ<0,
∴12﹣4×2×(﹣k)<0,
∴1+8k<0,
∴k<﹣.
故选A.
一十.由实际问题抽象出一元二次方程(共1小题)
10.(2021•西宁)某市严格落实国家节水政策,2018年用水总量为6.5亿立方米,2020年用水总量为5.265亿立方米.设该市用水总量的年平均降低率是x,那么x满足的方程是( )
A.6.5(1﹣x)2=5.265 B.6.5(1+x)2=5.265
C.5.265(1﹣x)2=6.5 D.5.265(1+x)2=6.5
【解答】解:设该市用水总量的年平均降低率是x,
则2019年的用水量为6.5(1﹣x),
2020年的用水量为6.5(1﹣x)2,
故选:A.
一十一.函数的图象(共1小题)
11.(2022•西宁)如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
A.
B.
C.
D.
【解答】解:过点A向BC作AH⊥BC于点H,
根据相似比可知:=,
即EF=2(3﹣x)
所以y=×2(3﹣x)x=﹣x2+3x=﹣(x﹣)2+.
∴y与x的关系式为:y=﹣(x﹣)2+.
纵观各选项,只有(A)选项图象符合.
故选:A.
一十二.动点问题的函数图象(共1小题)
12.(2021•西宁)如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,△APC的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
A.cm B.3cm C.4cm D.6cm
【解答】解:由图2可知,AB=acm,BC=4 cm,当点P到达点B时,△APC的面积为6cm2,
∴•AB•BC=6,即•a•4=6,
解得a=3 cm.
即AB的长为3cm.
故选:B.
一十三.一次函数的应用(共1小题)
13.(2020•西宁)全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( )
A.60米/分,40米/分 B.80米/分,60米/分
C.80米/分,40米/分 D.120米/分,80米/分
【解答】解:根据题意可知,甲每分钟比乙快:200÷10=20(米),
设乙的速度为x米/分,则甲的速度为(x+20)米/分,
根据题意得:2x+2(x+20)=200,
解得x=40,
40+20=60(米/分),
即甲的速度为60米/分,乙的速度为40米/分,
故选:A.
一十四.二次函数的图象(共1小题)
14.(2020•西宁)函数y=ax2+1和y=ax+a(a为常数,且a≠0),在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
【解答】解:∵y=ax2+1,
∴二次函数y=ax2+1的图象的顶点为(0,1),故A、B不符合题意;
当y=ax+a=0时,x=﹣1,
∴一次函数y=ax+a的图象过点(﹣1,0),故C不符题意,D符合题意.
故选:D.
一十五.三角形三边关系(共1小题)
15.(2022•西宁)若长度是4,6,a的三条线段能组成一个三角形,则a的值可以是( )
A.2 B.5 C.10 D.11
【解答】解:∵长度是4,6,a的三条线段能组成一个三角形,
∴6﹣4<a<6+4,
∴2<a<10,
∴只有选项B符合题意,选项A、选项C、选项D都不符合题意;
故选:B.
一十六.全等三角形的判定与性质(共1小题)
16.(2022•西宁)如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( )
A.△AOB是等边三角形 B.PE=PF
C.△PAE≌△PBF D.四边形OAPB是菱形
【解答】解:∵以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B,
∴OA=OB,
∵∠MON=60°,
∴△AOB是等边三角形,
∴A的结论正确,不符合题意;
∵分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,
∴PA=PB,
在△OPA和△OPB中,
,
∴△OPA≌△OPB(SSS),
∴∠POA=∠POB.
∵PE⊥OM,PF⊥ON,
∴PE=PF.
∴B的结论正确,不符合题意;
∵PE⊥OM,PF⊥ON,
∴∠PEA=∠PFB=90°.
在Rt△PAE和Rt△PBF中,
,
∴Rt△PAE≌Rt△PBF(HL).
∴③的结论正确,不符合题意;
由作图过程可知:OB与PB不一定相等,
∴四边形OAPB是菱形不成立,
∴④的结论错误,符合题意,
故选:D.
一十七.切线长定理(共1小题)
17.(2020•西宁)如图,PA,PB与⊙O分别相切于点A,B,PA=2,∠P=60°,则AB=( )
A. B.2 C. D.3
【解答】解:∵PA,PB与⊙O分别相切于点A,B,
∴PA=PB,∵∠APB=60°,
∴△PAB是等边三角形,
∴AB=AP=2.
故选:B.
一十八.三角形的内切圆与内心(共1小题)
18.(2021•西宁)如图,△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,连接OE,OF,∠C=90°,AC=6,BC=8,则阴影部分的面积为( )
A. B. C.4﹣π D.
【解答】解:连结AO、BO、DO,CO,设⊙O半径为r,
∵∠C=90°,AC=6,BC=8,
∴AB=10,
∵△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,
∴AC⊥OF,AB⊥OD,BC⊥OE,且OF=OD=OE=r,
∴S△ABC=S△ABO+S△ACO+S△BCO
∴=,
∴r==2,
∵∠C=90°,∠OFC=∠OEC=90°,OF=OE
∴四边形OFCE是正方形,
∴∠FOE=90°,
∴S阴影=S正方形OFCE﹣S扇形OFE=4﹣=4﹣π,
故选:C.
一十九.命题与定理(共1小题)
19.(2021•西宁)下列命题是真命题的是( )
A.同位角相等
B.是分式
C.数据6,3,10的中位数是3
D.第七次全国人口普查是全面调查
【解答】解:A、两直线平行,同位角相等,故原命题错误,是假命题,不符合题意;
B、是单项式,单项式是整式,故原命题错误,是假命题,不符合题意;
C、数据6,3,10的中位数是6,故原命题错误,是假命题,不符合题意;
D、第七次全国人口普查是全面调查,正确,是真命题,符合题意;
故选:D.
二十.翻折变换(折叠问题)(共1小题)
20.(2020•西宁)如图,在矩形ABCD中,AB=5,BC=6,点M,N分别在AD,BC上,且AM=BN,AD=3AM,E为BC边上一动点,连接DE,将△DCE沿DE所在直线折叠得到△DC′E,当C′点恰好落在线段MN上时,CE的长为( )
A.或2 B. C.或2 D.
【解答】解:设CE=x,则C′E=x,
∵矩形ABCD中,AB=5,
∴CD=AB=5,AD=BC=6,AD∥BC,
∵点M,N分别在AD,BC上,且3AM=AD,BN=AM,
∴DM=CN=4,
∴四边形CDMN为平行四边形,
∵∠NCD=90°,
∴四边形MNCD是矩形,
∴∠DMN=∠MNC=90°,MN=CD=5
由折叠知,C′D=CD=5,
∴MC′===3,
∴C′N=5﹣3=2,
∵EN=CN﹣CE=4﹣x,
∴C′E2﹣NE2=C′N2,
∴x2﹣(4﹣x)2=22,
解得,x=,即CE=.
故选:B.
二十一.中心对称图形(共1小题)
21.(2021•西宁)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.三角形 B.等边三角形 C.平行四边形 D.菱形
【解答】解:A.三角形不一定是轴对称图形,不是中心对称图形,故本选项不合题意;
B.等边三角形是轴对称图形,不是中心对称图形,故本选项不合题意;
C.平行四边形不是轴对称图形,是中心对称图形,故本选项不合题意;
D.菱形既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
二十二.简单几何体的三视图(共1小题)
22.(2020•西宁)在我国古代数学名著《九章算术》中,将底面为矩形、一条侧棱垂直于底面的四棱锥称之为“阳马”(如图).“阳马”的俯视图是( )
A. B.
C. D.
【解答】解:“阳马”的俯视图是一个矩形,还有一条看得见的棱,
故选:A.
二十三.由三视图判断几何体(共1小题)
23.(2021•西宁)某几何体的三视图如图所示,则此几何体是( )
A.圆锥 B.长方体 C.圆柱 D.四棱柱
【解答】解:∵主视图和左视图均为矩形,
∴该几何体为柱体,
∵俯视图为圆,
∴该几何体为圆柱,
故选:C.
二十四.众数(共1小题)
24.(2022•西宁)家务劳动是劳动教育的一个重要方面,教育部基础教育司发布通知要求家长引导孩子力所能及地做一些家务劳动.某校为了解七年级学生平均每周在家的劳动时间,随机抽取了部分七年级学生进行调查,根据调查结果,绘制了如下频数分布表:
组别
一
二
三
四
劳动时间x/h
0≤x<1
1≤x<2
2≤x<3
x≥3
频数
10
20
12
8
根据表中的信息,下列说法正确的是( )
A.本次调查的样本容量是50人
B.本次调查七年级学生平均每周在家劳动时间的中位数落在二组
C.本次调查七年级学生平均每周在家劳动时间的众数落在四组
D.若七年级共有500名学生,估计平均每周在家劳动时间在四组的学生大约有100人
【解答】解:A.本次调查的样本容量是50,原说法错误,故本选项不合题意;
B.本次调查七年级学生平均每周在家劳动时间的中位数落在二组,说法正确,故本选项符合题意;
C.无法判断本次调查七年级学生平均每周在家劳动时间的众数落在哪一组,原说法错误,故本选项不合题意;
D.若七年级共有500名学生,估计平均每周在家劳动时间在四组的学生大约有500×=80(人),原说法错误,故本选项不合题意.
故选:B.
青海省西宁市三年(2020-2022)中考数学真题分类汇编-选择题(含解析): 这是一份青海省西宁市三年(2020-2022)中考数学真题分类汇编-选择题(含解析),共27页。
青海省西宁市三年(2020-2022)中考数学真题分类汇编-解答题: 这是一份青海省西宁市三年(2020-2022)中考数学真题分类汇编-解答题,共37页。试卷主要包含了﹣1,先化简,再求值,计算,=x﹣2,解方程等内容,欢迎下载使用。
青海省西宁市三年(2020-2022)中考数学真题分类汇编-填空题: 这是一份青海省西宁市三年(2020-2022)中考数学真题分类汇编-填空题,共17页。试卷主要包含了﹣的绝对值是 ,2020= ,9的算术平方根是 ,= ,3﹣6a2•a4= 等内容,欢迎下载使用。













