广西河池三年（2020-2022）中考数学真题分类汇编-01选择题

这是一份广西河池三年（2020-2022）中考数学真题分类汇编-01选择题，共24页。

广西河池三年（2020-2022）中考数学真题分类汇编-01选择题
一．正数和负数（共2小题）
1．（2022•河池）如果将“收入50元”记作“+50元”，那么“支出20元”记作（　　）
A．+20元 B．﹣20元 C．+30元 D．﹣30元
2．（2020•河池）如果收入10元记作+10元，那么支出10元记作（　　）
A．+20 元 B．+10元 C．﹣10元 D．﹣20元
二．无理数（共1小题）
3．（2021•河池）下列4个实数中，为无理数的是（　　）
A．﹣2 B．0 C． D．3.14
三．同类项（共1小题）
4．（2021•河池）下列各式中，与2a2b为同类项的是（　　）
A．﹣2a2b B．﹣2ab C．2ab2 D．2a2
四．同底数幂的除法（共1小题）
5．（2022•河池）下列运算中，正确的是（　　）
A．x2+x2＝x4 B．3a3•2a2＝6a6
C．6y6÷2y2＝3y3 D．（﹣b2）3＝﹣b6
五．单项式乘单项式（共1小题）
6．（2020•河池）下列运算，正确的是（　　）
A．a（﹣a）＝﹣a2 B．（a2）3＝a5 C．2a﹣a＝1 D．a2+a＝3a
六．因式分解-运用公式法（共1小题）
7．（2022•河池）多项式x2﹣4x+4因式分解的结果是（　　）
A．x（x﹣4）+4 B．（x+2）（x﹣2） C．（x+2）2 D．（x﹣2）2
七．提公因式法与公式法的综合运用（共1小题）
8．（2021•河池）下列因式分解正确的是（　　）
A．a2+b2＝（a+b）2 B．a2+2ab+b2＝（a﹣b）2
C．a2﹣a＝a（a+1） D．a2﹣b2＝（a+b）（a﹣b）
八．二次根式有意义的条件（共1小题）
9．（2020•河池）若y＝有意义，则x的取值范围是（　　）
A．x＞0 B．x≥0 C．x＞2 D．x≥2
九．根的判别式（共1小题）
10．（2021•河池）关于x的一元二次方程x2+mx﹣m﹣2＝0的根的情况是（　　）
A．有两个不相等的实数根
B．有两个相等的实数根
C．没有实数根
D．实数根的个数由m的值确定
一十．由实际问题抽象出一元二次方程（共1小题）
11．（2022•河池）某厂家今年一月份的口罩产量是30万个，三月份的口罩产量是50万个，若设该厂家一月份到三月份的口罩产量的月平均增长率为x．则所列方程为（　　）
A．30（1+x）2＝50 B．30（1﹣x）2＝50
C．30（1+x2）＝50 D．30（1﹣x2）＝50
一十一．一元二次方程的应用（共1小题）
12．（2020•河池）某年级举办篮球友谊赛，参赛的每两个队之间都要比赛一场，共要比赛36场，则参加此次比赛的球队数是（　　）
A．6 B．7 C．8 D．9
一十二．解一元一次不等式组（共2小题）
13．（2021•河池）关于x的一元一次不等式组的解集如图所示，则它的解集是（　　）

A．x＞1 B．x≥1 C．x＞3 D．x≥3
14．（2020•河池）不等式组的解集在数轴上表示正确的是（　　）
A．
B．
C．
D．
一十三．点的坐标（共1小题）
15．（2022•河池）如果点P（m，1+2m）在第三象限内，那么m的取值范围是（　　）
A．﹣＜m＜0 B．m＞﹣ C．m＜0 D．m＜﹣
一十四．函数的图象（共1小题）
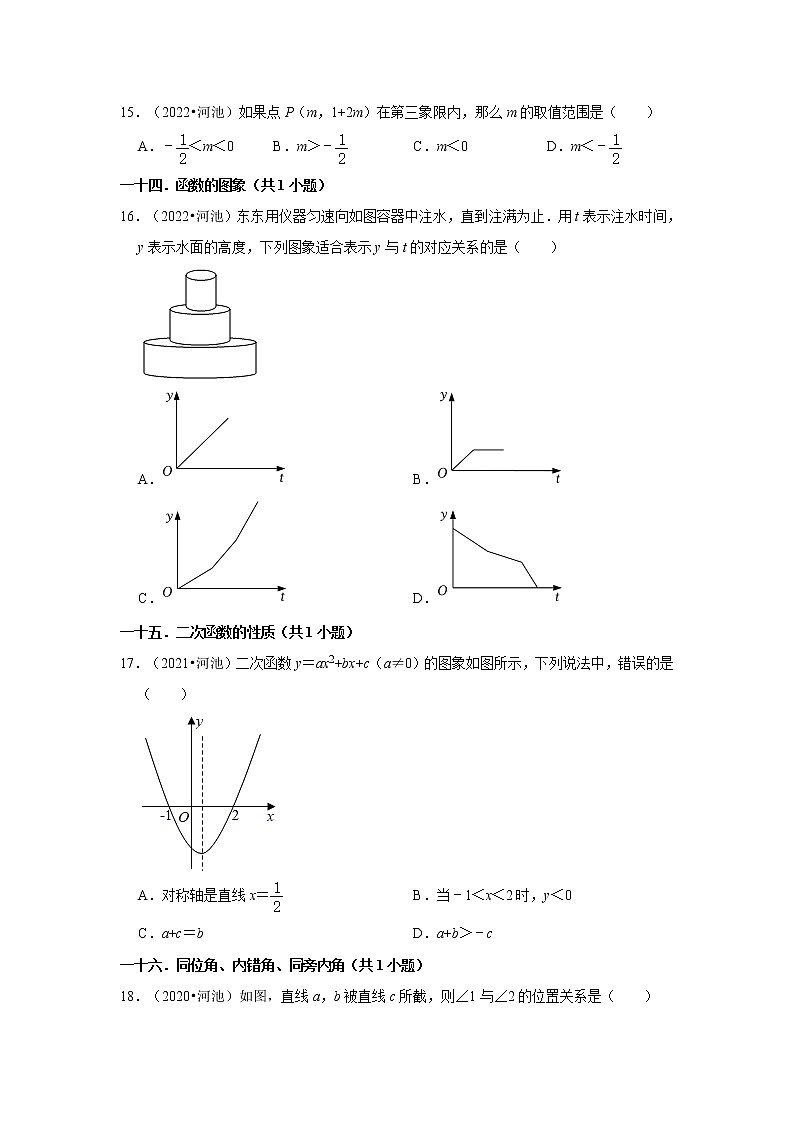
16．（2022•河池）东东用仪器匀速向如图容器中注水，直到注满为止．用t表示注水时间，y表示水面的高度，下列图象适合表示y与t的对应关系的是（　　）

A． B．
C． D．
一十五．二次函数的性质（共1小题）
17．（2021•河池）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列说法中，错误的是（　　）

A．对称轴是直线x＝ B．当﹣1＜x＜2时，y＜0
C．a+c＝b D．a+b＞﹣c
一十六．同位角、内错角、同旁内角（共1小题）
18．（2020•河池）如图，直线a，b被直线c所截，则∠1与∠2的位置关系是（　　）

A．同位角 B．内错角 C．同旁内角 D．邻补角
一十七．平行线的性质（共1小题）
19．（2022•河池）如图，平行线a，b被直线c所截，若∠1＝142°，则∠2的度数是（　　）

A．142° B．132° C．58° D．38°
一十八．三角形的外角性质（共1小题）
20．（2021•河池）如图，∠A＝40°，∠CBD是△ABC的外角，∠CBD＝120°，则∠C的大小是（　　）

A．90° B．80° C．60° D．40°
一十九．勾股定理（共1小题）
21．（2020•河池）如图，AB是⊙O的直径，CD是弦，AE⊥CD于点E，BF⊥CD于点F．若FB＝FE＝2，FC＝1，则AC的长是（　　）

A． B． C． D．
二十．平行四边形的性质（共1小题）
22．（2020•河池）如图，在▱ABCD中，CE平分∠BCD，交AB于点E，EA＝3，EB＝5，ED＝4．则CE的长是（　　）

A．5 B．6 C．4 D．5
二十一．菱形的性质（共1小题）
23．（2022•河池）如图，在菱形ABCD中，对角线AC，BD相交于点O，下列结论中错误的是（　　）

A．AB＝AD B．AC⊥BD C．AC＝BD D．∠DAC＝∠BAC
二十二．矩形的判定（共1小题）
24．（2021•河池）已知▱ABCD，下列条件中，不能判定这个平行四边形为矩形的是（　　）
A．∠A＝∠B B．∠A＝∠C C．AC＝BD D．AB⊥BC
二十三．正方形的性质（共1小题）
25．（2021•河池）如图，在边长为4的正方形ABCD中，点E，F分别在CD，AC上，BF⊥EF，CE＝1，则AF的长是（　　）

A． B． C． D．
二十四．切线的性质（共1小题）
26．（2022•河池）如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC＝25°，OC的延长线交PA于点P，则∠P的度数是（　　）

A．25° B．35° C．40° D．50°
二十五．作图—基本作图（共1小题）
27．（2020•河池）观察下列作图痕迹，所作CD为△ABC的边AB上的中线是（　　）
A． B．
C． D．
二十六．旋转的性质（共1小题）
28．（2022•河池）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，将Rt△ABC绕点B顺时针旋转90°得到Rt△A'B'C'．在此旋转过程中Rt△ABC所扫过的面积为（　　）

A．25π+24 B．5π+24 C．25π D．5π
二十七．中心对称图形（共1小题）
29．（2021•河池）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
二十八．锐角三角函数的定义（共1小题）
30．（2020•河池）在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，则sinB的值是（　　）
A． B． C． D．
二十九．简单几何体的三视图（共2小题）
31．（2022•河池）下列几何体中，三视图的三个视图完全相同的几何体是（　　）
A． B．
C． D．
32．（2020•河池）下列立体图形中，主视图为矩形的是（　　）
A． B． C． D．
三十．简单组合体的三视图（共1小题）
33．（2021•河池）如图是由几个小正方体组成的几何体，它的左视图是（　　）

A． B． C． D．
三十一．加权平均数（共1小题）
34．（2022•河池）希望中学规定学生的学期体育成绩满分为100，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%．若小强的三项成绩（百分制）依次是95，90，91．则小强这学期的体育成绩是（　　）
A．92 B．91.5 C．91 D．90
三十二．众数（共1小题）
35．（2020•河池）某学习小组7名同学的《数据的分析》一章的测验成绩如下（单位：分）：85，90，89，85，98，88，80，则该组数据的众数、中位数分别是（　　）
A．85，85 B．85，88 C．88，85 D．88，88
三十三．方差（共1小题）
36．（2021•河池）甲、乙、丙、丁4名同学参加跳远测试各10次，他们的平均成绩及其方差如表：
测试者
平均成绩（单位：m）
方差
甲
6.2
0.32
乙
6.0
0.58
丙
5.8
0.12
丁
6.2
0.25
若从其中选出1名成绩好且发挥稳定的同学参加学校运动会，则应选（　　）
A．甲 B．乙 C．丙 D．丁

参考答案与试题解析
一．正数和负数（共2小题）
1．（2022•河池）如果将“收入50元”记作“+50元”，那么“支出20元”记作（　　）
A．+20元 B．﹣20元 C．+30元 D．﹣30元
【解答】解：∵收入50元，记作“+50元”．
且收入跟支出意义互为相反．
∴支出20元，记作“﹣20元”．
故选：B．
2．（2020•河池）如果收入10元记作+10元，那么支出10元记作（　　）
A．+20 元 B．+10元 C．﹣10元 D．﹣20元
【解答】解：如果收入10元记作+10元，那么支出10元记作﹣10元．
故选：C．
二．无理数（共1小题）
3．（2021•河池）下列4个实数中，为无理数的是（　　）
A．﹣2 B．0 C． D．3.14
【解答】解：A．﹣2是整数，属于有理数，故本选项不合题意；
B.0是整数，属于有理数，故本选项不合题意；
C.是无理数，故本选项符合题意；
D.3.14有限小数，属于有理数，故本选项不合题意；
故选：C．
三．同类项（共1小题）
4．（2021•河池）下列各式中，与2a2b为同类项的是（　　）
A．﹣2a2b B．﹣2ab C．2ab2 D．2a2
【解答】解：2a2b中含有两个字母：a、b，且a的指数是2，b的指数是1，观察选项，与2a2b是同类项的是﹣2a2b．
故选：A．
四．同底数幂的除法（共1小题）
5．（2022•河池）下列运算中，正确的是（　　）
A．x2+x2＝x4 B．3a3•2a2＝6a6
C．6y6÷2y2＝3y3 D．（﹣b2）3＝﹣b6
【解答】解：A、原式＝2x2，不符合题意；
B、原式＝6a5，不符合题意；
C、原式＝3y4，不符合题意；
D、原式＝﹣b6，符合题意．
故选：D．
五．单项式乘单项式（共1小题）
6．（2020•河池）下列运算，正确的是（　　）
A．a（﹣a）＝﹣a2 B．（a2）3＝a5 C．2a﹣a＝1 D．a2+a＝3a
【解答】解：A、a（﹣a）＝﹣a2，原计算正确，故此选项符合题意；
B、（a2）3＝a6，原计算错误，故此选项不符合题意；
C、2a﹣a＝a，原计算错误，故此选项不符合题意；
D、a2与a不是同类项，不能合并，原计算错误，故此选项不符合题意；
故选：A．
六．因式分解-运用公式法（共1小题）
7．（2022•河池）多项式x2﹣4x+4因式分解的结果是（　　）
A．x（x﹣4）+4 B．（x+2）（x﹣2） C．（x+2）2 D．（x﹣2）2
【解答】解：原式＝（x﹣2）2．
故选：D．
七．提公因式法与公式法的综合运用（共1小题）
8．（2021•河池）下列因式分解正确的是（　　）
A．a2+b2＝（a+b）2 B．a2+2ab+b2＝（a﹣b）2
C．a2﹣a＝a（a+1） D．a2﹣b2＝（a+b）（a﹣b）
【解答】解：A．a2+b2无法分解因式，故此选项不合题意；
B．a2+2ab+b2＝（a+b）2，故此选项不合题意；
C．a2﹣a＝a（a﹣1），故此选项不合题意；
D．a2﹣b2＝（a+b）（a﹣b），故此选项符合题意．
故选：D．
八．二次根式有意义的条件（共1小题）
9．（2020•河池）若y＝有意义，则x的取值范围是（　　）
A．x＞0 B．x≥0 C．x＞2 D．x≥2
【解答】解：由题意得，2x≥0，
解得x≥0．
故选：B．
九．根的判别式（共1小题）
10．（2021•河池）关于x的一元二次方程x2+mx﹣m﹣2＝0的根的情况是（　　）
A．有两个不相等的实数根
B．有两个相等的实数根
C．没有实数根
D．实数根的个数由m的值确定
【解答】解：∵Δ＝m2﹣4（﹣m﹣2）
＝m2+4m+8
＝（m+2）2+4＞0，
∴方程有两个不相等的实数根．
故选：A．
一十．由实际问题抽象出一元二次方程（共1小题）
11．（2022•河池）某厂家今年一月份的口罩产量是30万个，三月份的口罩产量是50万个，若设该厂家一月份到三月份的口罩产量的月平均增长率为x．则所列方程为（　　）
A．30（1+x）2＝50 B．30（1﹣x）2＝50
C．30（1+x2）＝50 D．30（1﹣x2）＝50
【解答】解：设该厂家一月份到三月份的口罩产量的月平均增长率为x，
由题意得，30（1+x）2＝50．
故选：A．
一十一．一元二次方程的应用（共1小题）
12．（2020•河池）某年级举办篮球友谊赛，参赛的每两个队之间都要比赛一场，共要比赛36场，则参加此次比赛的球队数是（　　）
A．6 B．7 C．8 D．9
【解答】解：设参加此次比赛的球队数为x队，根据题意得：
x（x﹣1）＝36，
化简，得x2﹣x﹣72＝0，
解得x1＝9，x2＝﹣8（舍去），
∴参加此次比赛的球队数是9队．
故选：D．
一十二．解一元一次不等式组（共2小题）
13．（2021•河池）关于x的一元一次不等式组的解集如图所示，则它的解集是（　　）

A．x＞1 B．x≥1 C．x＞3 D．x≥3
【解答】解：由数轴知x＞3，
故选：C．
14．（2020•河池）不等式组的解集在数轴上表示正确的是（　　）
A．
B．
C．
D．
【解答】解：，
由①得：x＞1，
由②得：x≤4，
不等式组的解集为：1＜x≤4，
故选：D．
一十三．点的坐标（共1小题）
15．（2022•河池）如果点P（m，1+2m）在第三象限内，那么m的取值范围是（　　）
A．﹣＜m＜0 B．m＞﹣ C．m＜0 D．m＜﹣
【解答】解：根据题意得，
解①得m＜0，
解②得m＜．
则不等式组的解集是m＜﹣．
故选：D．
一十四．函数的图象（共1小题）
16．（2022•河池）东东用仪器匀速向如图容器中注水，直到注满为止．用t表示注水时间，y表示水面的高度，下列图象适合表示y与t的对应关系的是（　　）

A． B．
C． D．
【解答】解：因为底部的圆柱底面半径较大，所以刚开始水面上升比较慢，中间部分的圆柱底面半径较小，故水面上升较快，上部的圆柱的底面半径最小，所以水面上升最快，故适合表示y与t的对应关系的是选项C．
故选：C．
一十五．二次函数的性质（共1小题）
17．（2021•河池）二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列说法中，错误的是（　　）

A．对称轴是直线x＝ B．当﹣1＜x＜2时，y＜0
C．a+c＝b D．a+b＞﹣c
【解答】解：A、对称轴是直线x＝＝，故选项A不符合题意；
B、由函数图象知，当﹣1＜x＜2时，函数图象在x轴的下方，
∴当﹣1＜x＜2时，y＜0，故选项B不符合题意；
C、由图可知：当x＝﹣1时，y＝a﹣b+c＝0，
∴a+c＝b，故选项C不符合题意；
D、由图可知：当x＝1时，y＝a+b+c＜0，
∴a+b＜﹣c，故选项D符合题意；
故选：D．
一十六．同位角、内错角、同旁内角（共1小题）
18．（2020•河池）如图，直线a，b被直线c所截，则∠1与∠2的位置关系是（　　）

A．同位角 B．内错角 C．同旁内角 D．邻补角
【解答】解：如图所示，∠1和∠2两个角都在被截直线b和a同侧，并且在第三条直线c（截线）的同旁，故∠1和∠2是直线b、a被c所截而成的同位角．
故选：A．
一十七．平行线的性质（共1小题）
19．（2022•河池）如图，平行线a，b被直线c所截，若∠1＝142°，则∠2的度数是（　　）

A．142° B．132° C．58° D．38°
【解答】解：∵a∥b，
∴∠2＝∠1＝142°．
故选：A．
一十八．三角形的外角性质（共1小题）
20．（2021•河池）如图，∠A＝40°，∠CBD是△ABC的外角，∠CBD＝120°，则∠C的大小是（　　）

A．90° B．80° C．60° D．40°
【解答】解：由三角形的外角性质得，∠C＝∠CBD﹣∠A＝120°﹣40°＝80°．
故选：B．
一十九．勾股定理（共1小题）
21．（2020•河池）如图，AB是⊙O的直径，CD是弦，AE⊥CD于点E，BF⊥CD于点F．若FB＝FE＝2，FC＝1，则AC的长是（　　）

A． B． C． D．
【解答】解：连接BC，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠ACE+∠BCF＝90°，
∵BF⊥CD，
∴∠CFB＝90°，
∴∠CBF+∠BCF＝90°，
∴∠ACE＝∠CBF，
∵AE⊥CD，
∴∠AEC＝∠CFB＝90°，
∴△ACE∽△CBF，
∴，
∵FB＝FE＝2，FC＝1，
∴CE＝CF+EF＝3，BC＝＝＝，
∴＝，
∴AC＝，
故选：B．

二十．平行四边形的性质（共1小题）
22．（2020•河池）如图，在▱ABCD中，CE平分∠BCD，交AB于点E，EA＝3，EB＝5，ED＝4．则CE的长是（　　）

A．5 B．6 C．4 D．5
【解答】解：∵CE平分∠BCD，
∴∠BCE＝∠DCE，
∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝BC，AB∥CD，
∴∠BEC＝∠DCE，
∴∠BEC＝∠BCE，
∴BC＝BE＝5，
∴AD＝5，
∵EA＝3，ED＝4，
在△AED中，32+42＝52，即EA2+ED2＝AD2，
∴∠AED＝90°，
∴CD＝AB＝3+5＝8，∠EDC＝90°，
在Rt△EDC中，CE＝＝＝4．
故选：C．
二十一．菱形的性质（共1小题）
23．（2022•河池）如图，在菱形ABCD中，对角线AC，BD相交于点O，下列结论中错误的是（　　）

A．AB＝AD B．AC⊥BD C．AC＝BD D．∠DAC＝∠BAC
【解答】解：∵四边形ABCD是菱形，
∴∠BAC＝∠DAC，AB＝AD，AC⊥BD，
故A、B、D正确，无法得出AC＝BD，
故选：C．
二十二．矩形的判定（共1小题）
24．（2021•河池）已知▱ABCD，下列条件中，不能判定这个平行四边形为矩形的是（　　）
A．∠A＝∠B B．∠A＝∠C C．AC＝BD D．AB⊥BC
【解答】解：A、∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠A+∠B＝180°，
∵∠A＝∠B，
∴∠A＝∠B＝90°，
∴▱ABCD为矩形，故选项A不符合题意；
B、∠A＝∠C不能判定▱ABCD为矩形，故选项B符合题意；
C、∵四边形ABCD是平行四边形，AC＝BD，
∴▱ABCD是矩形，故选项C不符合题意；
D、∵AB⊥BC，
∴∠B＝90°，
∴▱ABCD为矩形，故选项D不符合题意；
故选：B．
二十三．正方形的性质（共1小题）
25．（2021•河池）如图，在边长为4的正方形ABCD中，点E，F分别在CD，AC上，BF⊥EF，CE＝1，则AF的长是（　　）

A． B． C． D．
【解答】解：过F作AB的垂线交AB于N，交CD于M，如图，
∵ABCD是正方形，
∴∠ABC＝∠BCD＝∠BNM＝90°，AB＝BC＝CD＝4，
∴四边形CMNB为矩形，
∴MN＝BC＝4，CM＝BN，
∵BF⊥EF，
∴∠EFB＝∠FNB＝90°，
∴∠FBN+∠NFB＝∠NFB+∠EFM，
∴∠FBN＝∠EFM，
∵四边形ABCD是正方形，
∴∠ACD＝45°，
∴∠MFC＝∠MCF＝45°，
∴MF＝MC＝NB，
在△MEF与△NFB中，
，
∴△MFE≌△NBF（ASA），
∴ME＝FN，
设ME＝FN＝x，则MC＝MF＝BN＝1+x，
∵MN＝MF+FN＝4，
∴1+x+x＝4，
∴x＝，
∴FN＝，
∵四边形ABCD为正方形，MN⊥AB，
∴∠NAF＝∠NFA＝45°，
∴FN＝AN，
∴AF＝＝FN＝，
故选：B．

二十四．切线的性质（共1小题）
26．（2022•河池）如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC＝25°，OC的延长线交PA于点P，则∠P的度数是（　　）

A．25° B．35° C．40° D．50°
【解答】解：∵∠ABC＝25°，
∴∠AOP＝2∠ABC＝50°，
∵PA是⊙O的切线，
∴PA⊥AB，
∴∠PAO＝90°，
∴∠P＝90°﹣∠AOP＝90°﹣50°＝40°，
故选：C．
二十五．作图—基本作图（共1小题）
27．（2020•河池）观察下列作图痕迹，所作CD为△ABC的边AB上的中线是（　　）
A． B．
C． D．
【解答】解：观察作图痕迹可知：
A．CD⊥AB，但不平分，
所以A选项不符合题意；
B．CD为△ABC的边AB上的中线，
所以B选项符合题意；
C．CD是∠ACB的平分线，
所以C选项不符合题意；
D．不符合基本作图过程，
所以D选项不符合题意．
故选：B．
二十六．旋转的性质（共1小题）
28．（2022•河池）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，将Rt△ABC绕点B顺时针旋转90°得到Rt△A'B'C'．在此旋转过程中Rt△ABC所扫过的面积为（　　）

A．25π+24 B．5π+24 C．25π D．5π
【解答】解：∵∠ACB＝90°，AC＝6，BC＝8，
∴AB＝10，
∴Rt△ABC所扫过的面积＝+×6×8＝25π+24，
故选：A．
二十七．中心对称图形（共1小题）
29．（2021•河池）下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
【解答】解：A．是轴对称图形，不是中心对称图形，故本选项不符合题意；
B．既是轴对称图形，又是中心对称图形，故本选项符合题意；
C．不是轴对称图形，是中心对称图形，故本选项不符合题意；
D．是轴对称图形，不是中心对称图形，故本选项不符合题意．
故选：B．
二十八．锐角三角函数的定义（共1小题）
30．（2020•河池）在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，则sinB的值是（　　）
A． B． C． D．
【解答】解：如图所示：
∵∠C＝90°，BC＝5，AC＝12，
∴AB＝＝13，
∴sinB＝＝．
故选：D．

二十九．简单几何体的三视图（共2小题）
31．（2022•河池）下列几何体中，三视图的三个视图完全相同的几何体是（　　）
A． B．
C． D．
【解答】解：A，三棱柱的三视图既有三角形又有长方形，故不符合题意；
B，圆柱的三视图既有圆又有长方形，故不符合题意；
C，圆锥的三视图既有三角形又有圆，故不符合题意；
D，球的三视图都是圆，故符合题意；
故选：D．
32．（2020•河池）下列立体图形中，主视图为矩形的是（　　）
A． B． C． D．
【解答】解：球体的主视图是圆形，圆台的主视图是等腰梯形，圆柱的主视图是矩形，圆锥的主视图是等腰三角形，
故选：C．
三十．简单组合体的三视图（共1小题）
33．（2021•河池）如图是由几个小正方体组成的几何体，它的左视图是（　　）

A． B． C． D．
【解答】解：从左边看，是一列3个小正方形．
故选：A．
三十一．加权平均数（共1小题）
34．（2022•河池）希望中学规定学生的学期体育成绩满分为100，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%．若小强的三项成绩（百分制）依次是95，90，91．则小强这学期的体育成绩是（　　）
A．92 B．91.5 C．91 D．90
【解答】解：根据题意得：
95×20%+90×30%+91×50%＝91.5（分）．
答：小强这学期的体育成绩是91.5分．
故选：B．
三十二．众数（共1小题）
35．（2020•河池）某学习小组7名同学的《数据的分析》一章的测验成绩如下（单位：分）：85，90，89，85，98，88，80，则该组数据的众数、中位数分别是（　　）
A．85，85 B．85，88 C．88，85 D．88，88
【解答】解：将数据85，90，89，85，98，88，80按照从小到大排列是：80，85，85，88，89，90，98，
故这组数据的众数是85，中位数是88，
故选：B．
三十三．方差（共1小题）
36．（2021•河池）甲、乙、丙、丁4名同学参加跳远测试各10次，他们的平均成绩及其方差如表：
测试者
平均成绩（单位：m）
方差
甲
6.2
0.32
乙
6.0
0.58
丙
5.8
0.12
丁
6.2
0.25
若从其中选出1名成绩好且发挥稳定的同学参加学校运动会，则应选（　　）
A．甲 B．乙 C．丙 D．丁
【解答】解：∵甲和丁的平均数比乙和丙的平均数大，
∴甲和丁的成绩较好，
∵S丁2＜S甲2，
∴丁的成绩比甲要稳定，
∴这四位同学中，成绩较好，且发挥稳定的是丁．
故选：D．