2021-2022学年湖南省岳阳市七年级（下）期末数学试卷（Word解析版）

2021-2022学年湖南省岳阳市七年级（下）期末数学试卷

一、选择题（本题共8小题，共24分）

1. 下面是疫情防控的知识图片，其中图案是轴对称图形的是(    )

A. 戴口罩讲卫生 B. 打喷嚏捂口鼻
C. 勤洗手勤通风 D. 有异常早就医

2. 下列运算结果正确的是(    )

A.  B.
C.  D.

3. 若是下列某个二元一次方程组的解，则这个方程组是(    )

A.  B.  C.  D.

4. 多项式可分解为，则的值是(    )

A.  B.  C.  D.

5. 将一副直角三角板按如图方式摆放，若直线，则的大小为(    )

A.
B.
C.
D.

6. 农科计划为某地选择合适的水果玉米种子，通过试验，甲、乙、丙、丁四种水果玉米种子每亩平均产量都是克，方差分别为，，，这四种水果玉米种子中产量最稳定的是(    )

A. 甲 B. 乙 C. 丙 D. 丁

7. 下列说法正确的是(    )

A. 垂线段最短
B. 平移改变图形的形状和大小
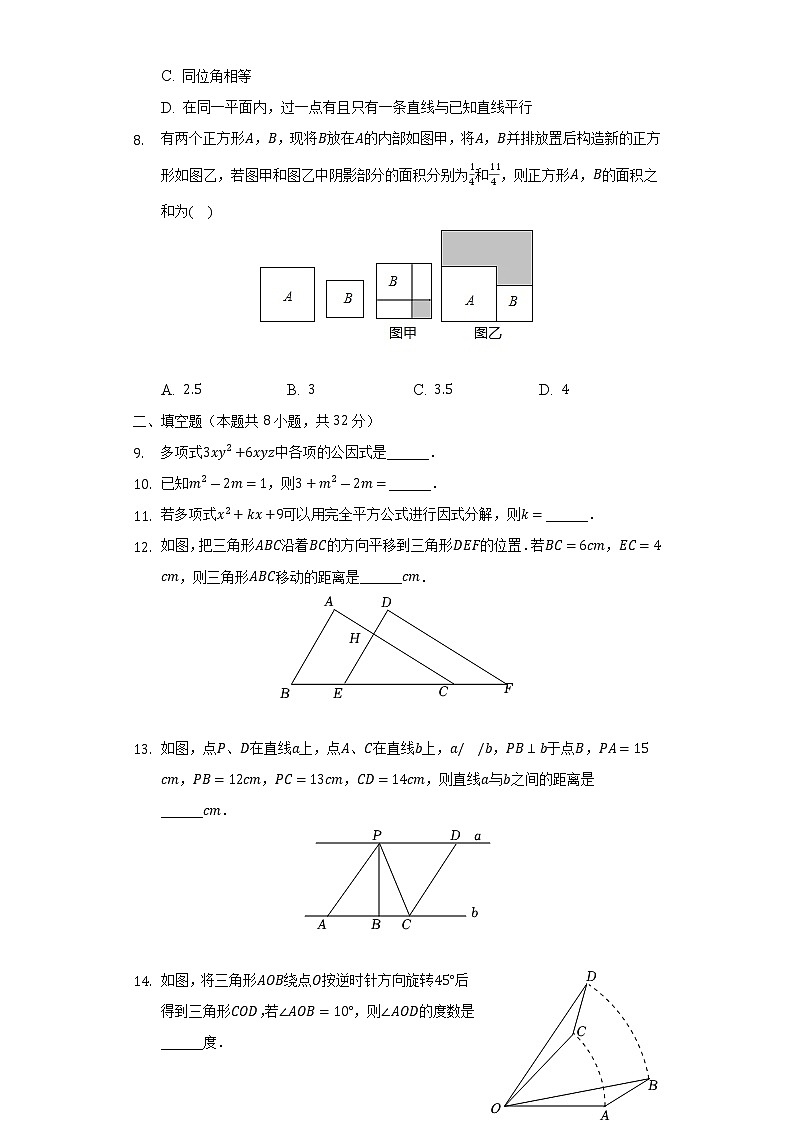
C. 同位角相等
D. 在同一平面内，过一点有且只有一条直线与已知直线平行

8. 有两个正方形，，现将放在的内部如图甲，将，并排放置后构造新的正方形如图乙，若图甲和图乙中阴影部分的面积分别为和，则正方形，的面积之和为(    )

A.  B.  C.  D.

二、填空题（本题共8小题，共32分）

9. 多项式中各项的公因式是______．
10. 已知，则______．
11. 若多项式可以用完全平方公式进行因式分解，则______．
12. 如图，把三角形沿着的方向平移到三角形的位置．若，，则三角形移动的距离是______．

13. 如图，点、在直线上，点、在直线上，，于点，，，，，则直线与之间的距离是______．

14. 如图，将三角形绕点按逆时针方向旋转后得到三角形，若，则的度数是______度．

15. 我国古代数学名著孙子算经中记载了一道题，大意是：匹马恰好拉了片瓦，已知匹大马能拉片瓦，匹小马能拉片瓦，问有多少匹大马、多少匹小马？若设大马有匹，小马有匹，那么可列方程组为______．

三、解答题（本题共8小题，共64分）

16. 已知，，，根据前面各式的规律，可得：
    ______．
    的值的个位数字是______．
17. 因式分解：
    ；
    ．
18. 请将下列证明过程补充完整：
    已知：如图，点在线段上，点在线段上，于点，于点，连接，．
    求证：．
    证明：于，于已知，
    ____________在同一平面内，垂直于同一条直线的两直线平行，
    ______，
    已知，
    ______，
    ______，
    ______

19. 解下列二元一次方程组：
    ；
    ．
20. 先化简，再求值：，其中，．
21. 从神舟五号到神舟十四号，年时光，中国航天人合力将中国太空梦化为现实，并不断取得突破性进展．为此，某中学开展以“中国梦航天梦”为主题的演讲比赛，赛后，某兴趣小组分别从七年级和八年级参赛选手中各随机抽取名同学，将他们的比赛成绩统计如图：
    
    根据图中信息，解答下列问题：
    七年级名被抽取的选手中，比赛成绩的中位数为______分；
    八年级名被抽取的选手中，比赛成绩的众数为______分；
    分别计算两个年级被抽取的选手的平均成绩，并估计哪个年级的平均成绩较高？
22. 如图，已知点在线段上，射线交直线于点，平分．
    若，求的度数．
    若，且，求证：．

23. 目前，新型冠状病毒在我国虽可控可防，但不可松懈，某校欲购置规格分别为和的甲、乙两种免洗手消毒液若干瓶，已知购买瓶甲和瓶乙免洗手消毒液需要元，购买瓶甲和瓶乙免洗手消毒液需要元．
    求甲、乙两种免洗手消毒液的单价．
    该校在校师生共人，平均每人每天都需使用的免洗手消毒液，若校方采购瓶甲和瓶乙免洗手消毒液共花费元，则这批消毒液可使用多少天？
    为节约成本，该校购买散装免洗手消毒液进行分装，现需将的免洗手消毒液全部装入最大容量分别为和的两种空瓶中两种瓶都装，每瓶均装满，若分装时平均每瓶需损耗，请问如何分装能使总损耗最小，求出此时需要的两种空瓶的数量．

24. 如图，已知和互为邻补角，，将一个三角板的直角顶点放在点处注：，．
    如图，使三角板的短直角边与射线重合，若，则______．
    如图，将图中的三角板绕点顺时针旋转，试判断此时与的位置关系，并说明理由．
    如图，将图中的三角板绕点顺时针旋转，使得，此时和满足什么关系？请说明理由．
    将图中的三角板绕点以每秒的速度沿顺时针方向旋转一周，在旋转的过程中，第秒时，恰好与直线重合，求的值用含的式子表示．
     

答案和解析

1.【答案】 

【解析】解：，，选项中的图形都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形．
选项中的图形能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形．
故选：．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
 

2.【答案】 

【解析】解：、原式，不符合题意；
B、原式，符合题意；
C、原式，不符合题意；
D、原式，不符合题意．
故选：．
各式计算得到结果，即可作出判断．
此题考查了完全平方公式，合并同类项，以及同底数幂的乘法，熟练掌握运算法则及公式是解本题的关键．
 

3.【答案】 

【解析】解：当，，则，，那么是的解，故A符合题意．
B.当，，则，，那么不是的解，故B不符合题意．
C.当，，则，，那么不是的解，故C不符合题意．
D.当，，则，，那么不是的解，故D不符合题意．
故选：．
根据二元一次方程组的解的定义解决此题．
本题主要考查二元一次方程组的解，熟练掌握二元一次方程组的解的定义是解决本题的关键．
 

4.【答案】 

【解析】解：

．
由题意得，．
．
故选：．
根据多项式乘多项式的乘法法则解决此题．
本题主要考查多项式乘多项式，熟练掌握多项式乘多项式的乘法法则是解决本题的关键．
 

5.【答案】 

【解析】解：如图：

，
，
，
．
故选：．
根据可知，进而可求出．
本题考查平行线的性质，解题关键是结合图形利用平行线的性质进行角的计算．
 

6.【答案】 

【解析】解：，，，
，
这四种水果玉米种子中产量最稳定的是丙，
故选：．
根据方差的意义求解即可．
本题主要考查方差，方差是反映一组数据的波动大小的一个量．方差越大，与平均值的离散程度越大，稳定性也越差；反之，则它与其平均值的离散程度越小，稳定性越好．
 

7.【答案】 

【解析】解：垂线段最短，即过直线外一点，到这条直线上各点的连线中，垂直线段最短，简称“垂线段最短”，因此选项A符合题意；
B.平移没有改变图形的形状和大小，只是改变了图形的位置，因此选项B不符合题意；
C.两直线平行，同位角相等，两直线不平行，则同位角不相等，因此选项C 不符合题意；
D.在同一平面内，过直线外一点有且只有一条直线与已知直线平行，因此选项D不符合题意；
故选：．
根据平移的性质，垂线段最短平行线的性质以及平行公理逐项进行判断即可．
本题考查平移的性质，垂线段最短平行线的性质以及平行公理，掌握平移的性质，垂线段最短，平行线的性质以及平行公理是正确判断的前提．
 

8.【答案】 

【解析】解：设正方形的边长为，正方形的边长为，
由题意得：，，
，，
，，
正方形，的面积之和为．
故选：．
设正方形的边长为，正方形的边长为，然后根据题意易得，，进而根据完全平方公式可进行求解．
本题主要考查完全平方公式与几何图形，熟练掌握完全平方公式的特征是解题的关键．
 

9.【答案】 

【解析】解：，
故答案为：．
根据公因式是各项中都含有的因式，可得答案．
此题考查的是公因式的定义，找公因式的要点是：公因式的系数是多项式各项系数的最大公约数；字母取各项都含有的相同字母；相同字母的指数取次数最低的．
 

10.【答案】 

【解析】解：，
；
故答案为：．
直接把代入计算，即可得到答案．
本题考查了求代数式的值，解题的关键是熟练掌握整体代入法进行解题．
 

11.【答案】 

【解析】解：多项式可以用完全平方公式进行因式分解，
，
．
故答案为：．
直接利用完全平方公式得出的值．
此题主要考查了公式法分解因式，正确运用乘法公式是解题关键．
 

12.【答案】 

【解析】解：三角形沿着的方向平移得到三角形，
，平移的距离为的长，
，
即，
，
三角形移动的距离是．
故答案为：．
根据平移的性质得到，平移的距离为的长，然后利用求出即可．
本题考查平移的性质：平移不改变图形的形状和大小；经过平移，对应点所连的线段平行或共线且相等，对应线段平行且相等，对应角相等．
 

13.【答案】 

【解析】解：，于点，，
根据平行线之间的距离可知，直线与之间的距离是．
故答案为：．
根据平行线之间的距离解答即可，从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离．
本题考查了平行线之间的距离，平行线之间的距离，从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离．平行线间的距离处处相等．
 

14.【答案】 

【解析】解：将三角形绕点按逆时针方向旋转后得到三角形，
，
，
故答案为：．
由旋转的性质可得，即可求解．
本题考查了旋转的性质，掌握旋转的性质是解题的关键．
 

15.【答案】 

【解析】解：设大马有匹，小马有匹，由题意得：
，
故答案为：．
设大马有匹，小马有匹，由题意得等量关系：共有马匹；大马拉瓦数小马拉瓦数，根据等量关系，列出方程组即可．
此题主要考查了由实际问题抽象出二元一次方程组，关键是正确理解题意，找出题目中的等量关系，再列出方程．
 

16.【答案】   

【解析】解：根据规律可得，
，
故答案为：；
由所列举等式的规律和等式的性质可得，
，
由于的个位数字为，
的个位数字为，
的个位数字为，
的个位数字为，
的个位数字为，

因为，
所以的个位数字为，
故答案为：．
根据规律得出答案；
得出结果为，再根据的个位数字所呈现的规律得出答案．
本题考查平方差公式以及数字的变化类，掌握平方差公式的结构特征以及代数式所呈现的规律是解决问题的前提．
 

17.【答案】解：；

；
． 

【解析】先提公因式，再利用平方差公式继续分解即可解答；
利用完全平方公式，进行分解即可解答．
本题考查了提公因式法与公式法的综合运用，一定要注意如果多项式的各项含有公因式，必须先提公因式．
 

18.【答案】    两直线平行，同位角相等  同旁内角互补，两直线平行  两直线平行，内错角相等  等量代换 

【解析】证明：于，于已知，
在同一平面内，垂直于同一条直线的两直线平行，
两直线平行，同位角相等，
已知，
同旁内角互补，两直线平行，
两直线平行，内错角相等，
等量代换．
故答案为：；；两直线平行，同位角相等；同旁内角互补，两直线平行；两直线平行，内错角相等；等量代换．
根据“在同一平面内，垂直于同一条直线的两直线平行”得到，根据“同旁内角互补，两直线平行”得到，根据平行线的性质定理得到，，等量代换即可得解．
此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．
 

19.【答案】解：，
将代入得，
，
解得，
即，
；
，
得，
，
解得，
将代入得，
，
． 

【解析】利用代入消元法解答即可；
利用加减消元法解答即可．
本题考查了解方程组，解题关键在于熟练利用加减消元法和代入消元法解二元一次方程组．
 

20.【答案】解：

，
当，时，原式

． 

【解析】先去括号，再合并同类项，然后把，的值代入化简后的式子进行计算即可解答．
本题考查了整式的混合运算化简求值，准确熟练地进行计算是解题的关键．
 

21.【答案】   

【解析】解：将七年级名学生成绩从小到大排列处在中间位置的一个数是分，因此中位数是分，
故答案为：；
八年级名学生的成绩出现次数最多的是分，共出现次，因此众数是分，
故答案为：；
七年级学生的平均成绩为：分，
八年级学生的平均成绩为：分，
因为，
所以七年级学生的成绩较好．
根据中位数的意义进行判断即可；
根据众数的意义进行计算即可；
根据平均数的计算方法进行计算即可．
本题考查中位数、众数、平均数，理解中位数、众数的意义，掌握平均数的计算方法是正确解答的前提．
 

22.【答案】解：平分，，
，
，
；
证明：，，
，
，
，
，
，
，
，
． 

【解析】根据角平分线的定义可知，求出的度数即可根据对顶角相等求出；
，，等量代换得，从而得出，根据平行线的性质得，根据得，即可证得．
本题考查了平行线的判定和性质以及角平分线的性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．
 

23.【答案】解：设甲种免洗手消毒液的单价为元，乙种免洗手消毒液的单价为元，
依题意得：，
解得：．
答：甲种免洗手消毒液的单价为元，乙种免洗手消毒液的单价为元．
，
元钱可购买的免洗手消毒液，
元共可购买免洗手消毒液，
可使用的时间为天．
答：这批消毒液可使用天．
设需要最大容量为的空瓶个，最大容量为的空瓶个，
依题意得：，

又，均为正整数，
或，
共有种分装方案，
方案：分装成瓶的瓶装消毒液，瓶的瓶装消毒液，总损耗为；
方案：分装成瓶的瓶装消毒液，瓶的瓶装消毒液，总损耗为．
，
当分装成瓶的瓶装消毒液，瓶的瓶装消毒液时总损耗最小，此时需要最大容量为的空瓶个，最大容量为的空瓶个． 

【解析】设甲种免洗手消毒液的单价为元，乙种免洗手消毒液的单价为元，根据“购买瓶甲和瓶乙免洗手消毒液需要元，购买瓶甲和瓶乙免洗手消毒液需要元”，即可得出关于，的二元一次方程组，解之即可得出结论；
由价格与含量成比例，可得出元钱可购买的免洗手消毒液，再求出元可购买免洗手消毒液的含量及可使用时间，即可得出结论；
设需要最大容量为的空瓶个，最大容量为的空瓶个，根据需分装的免洗手消毒液共且每瓶均装满，即可得出关于，的二元一次方程，结合，均为正整数，即可得出各分装方案，再求出各分装方案的总损耗，比较后即可得出结论．
本题考查了二元一次方程组的应用、有理数的混合运算以及二元一次方程的应用，解题的关键是：找准等量关系，正确列出二元一次方程组；根据各数量之间的关系，列式计算；找准等量关系，正确列出二元一次方程．
 

24.【答案】 

【解析】解：，，
，
故答案为：；
，
；
，
，
，
，
，
，
；
第秒时，恰好与直线重合，
则，
解得．
与互余，则两角之和为，根据的值解答即可；
，根据平行线的判定可知；
，则，根据已知可得，根据可求解；
根据题意列出关于的方程即可解答．
本题综合考查了平行线的判定、余角和补角，能根据图形和已知求出各个角的度数是解此题的关键．