

陕西省铜川市新区2021-2022学年七年级下学期期末质量检测数学试卷(word版含答案)
展开陕西省铜川市新区2021-2022学年七年级下学期期末质量检测
数学试卷
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.(3分)下列快递图标中,是轴对称图形的是( )
A. B.
C. D.
2.(3分)“谁知盘中餐,粒粒皆辛苦”,已知一粒米的重量约0.000021千克,将数据0.000021用科学记数法表示为( )
A.0.21×10﹣4 B.2.1×10﹣4 C.2.1×10﹣5 D.21×10﹣6
3.(3分)若一个角等于它的余角,则这个角的补角度数为( )
A.135° B.120° C.90° D.45°
4.(3分)下列计算正确的是( )
A.a4+a3=a7 B.(a3)2=a5
C.a6÷a3=a3 D.(a﹣b)2=a2﹣b2
5.(3分)书架上有2本英语书,3本数学书,4本语文书,从中任意取出一本是数学书的概率是( )
A. B. C. D.
6.(3分)如图,在△ABC和△ADC中,∠B=∠D=90°,∠1+∠2=90°,BC=3,则CD=( )
A.4 B.1 C.2 D.3
7.(3分)如图,在△ABC中,AB=3BC,BD平分∠ABC交AC于点D,若△ABD的面积为S1,△BCD的面积为S2,则关于S1与S2之间的数量关系,下列说法正确的是( )
A.S1=4S2 B.S1=3S2 C.S1=2S2 D.S1=S2
8.(3分)已知小婷的家、书店、学校在同一直线上,图中的信息反映的过程是:小婷从家跑步去书店,在书店购买书和文具后又走到学校取东西,然后再走回家,图中x表示时间,y表示小婷离家的距离,依据图中信息,下列说法错误的是( )
A.书店离小婷家2.5km
B.小婷在书店停留的时间是15min
C.书店离学校1km
D.小婷从学校出发后经过35min回到家
二、填空题(共5小题,每小题3分,计15分)
9.(3分)请你写出一个必然事件 .
10.(3分)已知△ABC中,AB=5,AC=7,BC=a,则a的取值范围是 .
11.(3分)用篱笆围一个面积为6a2﹣2a的长方形花圃,其中一条边长为2a,则与这条边相邻的边长为 .(用含a的代数式表示)
12.(3分)某院观众的座位按下列方式设置:
排数(x)
1
2
3
4
…
座位数(y)
30
33
36
39
…
根据表格中两个变量之间的关系,则当x=8时,y= .
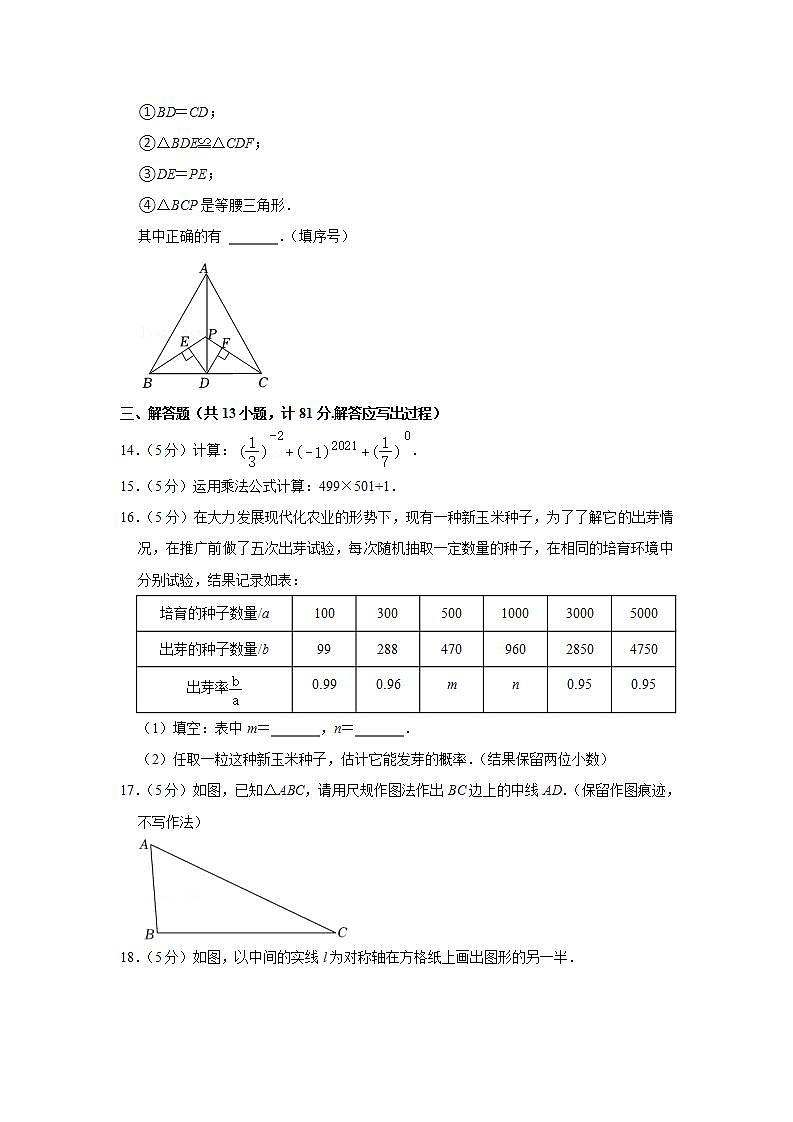
13.(3分)如图,在△ABC中,AB=AC,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作DE⊥BP,DF⊥CP,垂足分别为EF,则下列结论:
①BD=CD;
②△BDE≌△CDF;
③DE=PE;
④△BCP是等腰三角形.
其中正确的有 .(填序号)
三、解答题(共13小题,计81分.解答应写出过程)
14.(5分)计算:.
15.(5分)运用乘法公式计算:499×501+1.
16.(5分)在大力发展现代化农业的形势下,现有一种新玉米种子,为了了解它的出芽情况,在推广前做了五次出芽试验,每次随机抽取一定数量的种子,在相同的培育环境中分别试验,结果记录如表:
培育的种子数量/a
100
300
500
1000
3000
5000
出芽的种子数量/b
99
288
470
960
2850
4750
出芽率
0.99
0.96
m
n
0.95
0.95
(1)填空:表中m= ,n= .
(2)任取一粒这种新玉米种子,估计它能发芽的概率.(结果保留两位小数)
17.(5分)如图,已知△ABC,请用尺规作图法作出BC边上的中线AD.(保留作图痕迹,不写作法)
18.(5分)如图,以中间的实线l为对称轴在方格纸上画出图形的另一半.
19.(5分)如图,△ABC的顶点A、B和△DEF的顶点D、E在一条直线上,且∠A=∠EDF,∠C=∠F,请你再添加一个条件使得BC=EF,并说明理由.
20.(5分)先化简,再求值:[(3m+4n)(m+2n)﹣2n(2m+4n)]÷3m,其中m=3,n=1.
21.(6分)如图,已知AB∥CD,AH与BC交于点F,且点H在AD的延长线上,∠1=∠2.
(1)判断BC与DE平行吗?为什么?
(2)若∠1=110°,∠A=50°,求∠C的度数.
22.(7分)移动支付由于快捷便利已成为大家平时生活中非常普遍的支付方式.某超市除接收顾客的现金支付外,还支持“微信”“支付宝”“银行卡”“云闪付”四种支付方式,小马、小王和小张在该超市购完物后,都从“微信”、“支付宝”、“银行卡”、“云闪付”四种支付方式中随机选一种方式进行支付,每种方式被选择的可能性相同.
(1)求小马选择支付宝支付的概率;
(2)若小王选择了微信支付,求小张和小王选择同一种支付方式的概率.
23.(7分)如图为某单摆装置示意图,摆线长OA=OB=OC,当摆线位于OB位置时,过点B作BD⊥OA于点D,测得OD=15cm,当摆线位于OC位置时,OB与OC恰好垂直,求此时摆球到OA的水平距离CE的长(CE⊥OA).
24.(8分)如图,在△ABC中,∠A=40°,AB=AC,点D为AC上任意一点,若△BCD是以BC为腰的等腰三角形,求∠BDC的度数.
25.(8分)如图,在△ABC中,AD为BC边上的高,BC=8,AD=4,点P为边BC上一动点,连接AP,随着BP长度的变化,△ACP的面积也在变化.
(1)在这个变化过程中,自变量是什么?因变量是什么?
(2)若设BP=x,△ACP的面积为y,请写出y与x的关系式;
(3)当BP=AD时,求△ACP的面积.
26.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,D为AB边的中点,BE⊥BC交CD的延长线于点E,连接AE,过点A作AF平分∠BAC交CD于点F.
(1)试判断AF与BE之间的数量关系,并说明理由;
(2)∠EAF与∠AFC互补吗?若互补,请说明理由;若不互补,请写出∠EAF与∠AFC之间的数量关系.
陕西省铜川市新区2021-2022学年七年级下学期期末质量检测
数学试卷参考答案与试题解析
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.(3分)下列快递图标中,是轴对称图形的是( )
A. B.
C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A,B,C选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:D.
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.(3分)“谁知盘中餐,粒粒皆辛苦”,已知一粒米的重量约0.000021千克,将数据0.000021用科学记数法表示为( )
A.0.21×10﹣4 B.2.1×10﹣4 C.2.1×10﹣5 D.21×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【解答】解:0.000021=2.1×10﹣5.
故选:C.
【点评】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
3.(3分)若一个角等于它的余角,则这个角的补角度数为( )
A.135° B.120° C.90° D.45°
【分析】根据互余的两个角的和等于90°,互补的两个角的和等于180°解答.
【解答】解:一个角等于它的余角,这个角的度数是45°,
则这个角的补角的度数是180°﹣45°=135°.
故选:A.
【点评】本题主要考查了余角和补角,熟记概念是解题的关键.
4.(3分)下列计算正确的是( )
A.a4+a3=a7 B.(a3)2=a5
C.a6÷a3=a3 D.(a﹣b)2=a2﹣b2
【分析】A、根据合并同类项法则计算判断即可;
B、根据幂的乘方运算法则计算判断即可;
C、根据同底数幂的除法运算法则计算判断即可;
D、根据完全平方公式计算判断即可.
【解答】解:A、等号左侧两项不是同类项,不能合并,不合题意;
B、原式=a6,不合题意;
C、原式=a3,符合题意;
D、原式=a2﹣2ab+b2,不合题意;
故选:C.
【点评】此题考查的是合并同类项、幂的乘方运算、同底数幂的除法运算、完全平方公式,掌握其运算法则是解决此题的关键.
5.(3分)书架上有2本英语书,3本数学书,4本语文书,从中任意取出一本是数学书的概率是( )
A. B. C. D.
【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
【解答】解:从中任意抽取一本是数学书的概率是=.
故选:B.
【点评】本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.
6.(3分)如图,在△ABC和△ADC中,∠B=∠D=90°,∠1+∠2=90°,BC=3,则CD=( )
A.4 B.1 C.2 D.3
【分析】根据直角三角形的两锐角互余得到∠1=∠CAD,结合题意利用AAS证明△ABC≌△ADC,根据全等三角形的性质即可得解.
【解答】解:∵∠D=90°,
∴∠2+∠CAD=90°,
∵∠1+∠2=90°,
∴∠1=∠CAD,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(AAS),
∴BC=CD,
∵BC=3,
∴CD=3,
故选:D.
【点评】此题考查了全等三角形的判定与性质,熟记全等三角形的判定定理与性质定理是解题的关键.
7.(3分)如图,在△ABC中,AB=3BC,BD平分∠ABC交AC于点D,若△ABD的面积为S1,△BCD的面积为S2,则关于S1与S2之间的数量关系,下列说法正确的是( )
A.S1=4S2 B.S1=3S2 C.S1=2S2 D.S1=S2
【分析】过点D作DE⊥AB于E,DF⊥BC于F,由角平分线的性质得出DE=DF,根据三角形面积可得出答案.
【解答】解:过点D作DE⊥AB于E,DF⊥BC于F,
∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DE=DF,
∵S1=S△ABD=AB•DE,S2=S△DBC=BC•DF,
∴,
∵AB=3BC,
∴S1=3S2.
故选:B.
【点评】本题考查了角平分线的性质,三角形的面积,证出DE=DF是解题的关键.
8.(3分)已知小婷的家、书店、学校在同一直线上,图中的信息反映的过程是:小婷从家跑步去书店,在书店购买书和文具后又走到学校取东西,然后再走回家,图中x表示时间,y表示小婷离家的距离,依据图中信息,下列说法错误的是( )
A.书店离小婷家2.5km
B.小婷在书店停留的时间是15min
C.书店离学校1km
D.小婷从学校出发后经过35min回到家
【分析】由图可得书店与家的距离为2.5km,即可判断A选项,由图可得学校与家的距离为1.5km,由选项A即可判断B选项,由图可得学校回家花费的时间,由图可得学校回家的路程,求解即可判断C选项,由图可得书店到学校花费的时间,再由选项B即可判断D选项.
【解答】解:由图可得书店离小婷家2.5km,故A选项正确;
由图可得小婷在书店停留的时间为:30﹣15=15(min),故B选项正确;
由图可得学校离小婷家1.5km,即书店离学校的距离为2.5﹣1.5=1km,故C选项正确;
由图可得从学校回家所花时间为90﹣65=25(min),从学校回家的平均速度为1500÷25=60m/min,故C选项正确;
由图可得小婷从学校出发后经过90﹣65=25(min)回到家,故D选项错误;
故选:D.
【点评】本题考查了函数的图象,解题的关键是从图中得出各段距离以及时间.
二、填空题(共5小题,每小题3分,计15分)
9.(3分)请你写出一个必然事件 明天的太阳从东方升起. .
【分析】填写一个一定发生的事件即可.
【解答】解:明天的太阳从东方升起就是一个必然事件.
【点评】必然事件指在一定条件下一定发生的事件.
10.(3分)已知△ABC中,AB=5,AC=7,BC=a,则a的取值范围是 2<a<12 .
【分析】直接利用三角形三边关系得出a的取值范围.
【解答】解:∵△ABC中,AB=5,AC=7,BC=a,
∴7﹣5<a<7+5,
即2<a<12.
故答案为:2<a<12.
【点评】此题主要考查了三角形三边关系,正确记忆三角形边长之间的关系是解题关键.
11.(3分)用篱笆围一个面积为6a2﹣2a的长方形花圃,其中一条边长为2a,则与这条边相邻的边长为 3a﹣1 .(用含a的代数式表示)
【分析】先根据题意列出计算式,然后根据整式除法的运算法则计算即可.
【解答】解:另一边长为:(6a2﹣2a)÷2a=6a2÷2a﹣2a÷2a=3a﹣1.
故答案为:3a﹣1.
【点评】本题考查了整式除法,解题的关键是熟记法则并灵活运用.多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
12.(3分)某院观众的座位按下列方式设置:
排数(x)
1
2
3
4
…
座位数(y)
30
33
36
39
…
根据表格中两个变量之间的关系,则当x=8时,y= 51 .
【分析】依据表格中两个变量之间的关系,即可得到函数关系式,即可得到当x=8时,y的值为51.
【解答】解:由题可得,两个变量之间的关系为y=30+3(x﹣1),
∴当x=8时,y=30+3×7=51,
故答案为:51.
【点评】本题考查列代数式及相关代数式求值问题,根据相应规律得到函数关系式是解决本题的关键.
13.(3分)如图,在△ABC中,AB=AC,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作DE⊥BP,DF⊥CP,垂足分别为EF,则下列结论:
①BD=CD;
②△BDE≌△CDF;
③DE=PE;
④△BCP是等腰三角形.
其中正确的有 ①②④ .(填序号)
【分析】由等腰三角形的性质可得AD⊥BC,BD=CD,故①正确,由线段垂直平分线的性质可得BP=CP,即△BPC是等腰三角形,∠PBD=∠PCD,故④正确,由“AAS”可证△BDE≌△CDF,故②正确,即可求解.
【解答】解:∵AB=AC,点D是BC边的中点,
∴AD⊥BC,BD=CD,故①正确,
∴BP=CP,
∴△BPC是等腰三角形,∠PBD=∠PCD,故④正确,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),故②正确,
由题意无法证明DE=PE,故③错误,
故答案为:①②④.
【点评】本题考查了全等三角形的判定和性质,等腰三角形的性质,线段垂直平分线的性质,灵活运用这些性质解决问题是解题的关键.
三、解答题(共13小题,计81分.解答应写出过程)
14.(5分)计算:.
【分析】将原式进行乘方运算后,再进行加减法运算.
【解答】解:原式=9﹣1+1=9.
【点评】本题考查了实数的运算,解题关键在于正确的计算.
15.(5分)运用乘法公式计算:499×501+1.
【分析】利用平方差公式进行计算即可.
【解答】解:499×501+1
=(500﹣1)(500+1)+1
=5002﹣12+1
=250000﹣1+1
=250000.
【点评】本题考查了平方差公式的知识,注意在运算前仔细观察,看能否构造出平方差公式的形式.
16.(5分)在大力发展现代化农业的形势下,现有一种新玉米种子,为了了解它的出芽情况,在推广前做了五次出芽试验,每次随机抽取一定数量的种子,在相同的培育环境中分别试验,结果记录如表:
培育的种子数量/a
100
300
500
1000
3000
5000
出芽的种子数量/b
99
288
470
960
2850
4750
出芽率
0.99
0.96
m
n
0.95
0.95
(1)填空:表中m= 0.94 ,n= 0.96 .
(2)任取一粒这种新玉米种子,估计它能发芽的概率.(结果保留两位小数)
【分析】(1)用发芽的种子数量除以实验种子的数量即可求得m、n的值;
(2)用频率估计概率即可.
【解答】解:(1)m=470÷500=0.94;n=960÷1000=0.96;
故答案为:0.94,0.96.
(2)任取一粒这种新玉米种子,估计它能发芽的概率为0.95.
【点评】本题考查了利用频率估计概率的知识,解题的关键是了解大量重复试验中频率能估计概率,难度不大.
17.(5分)如图,已知△ABC,请用尺规作图法作出BC边上的中线AD.(保留作图痕迹,不写作法)
【分析】作线段BC的垂直平分线交BC于点D,连接AD.
【解答】解:如图,线段AD即为所求.
【点评】本题考查作图﹣基本作图,线段的垂直平分线等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
18.(5分)如图,以中间的实线l为对称轴在方格纸上画出图形的另一半.
【分析】分别作出A,B,E,F关于直线L的对称点C,D,G,H,连接CD,CH,DG即可.
【解答】解:如图,线段CD即为所求.
【点评】本题考查作图﹣轴对称变换,解题的关键是掌握轴对称变换的性质,属于中考常考题型.
19.(5分)如图,△ABC的顶点A、B和△DEF的顶点D、E在一条直线上,且∠A=∠EDF,∠C=∠F,请你再添加一个条件使得BC=EF,并说明理由.
【分析】添加条件AC=DF.由ASA证明△ABC≌△DEF即可.
【解答】解:答案不唯一.
添加的条件为AC=DF.
理由:在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
∴BC=EF.
【点评】本题考查了全等三角形的判定;熟练掌握全等三角形的判定方法是解决问题的关键.
20.(5分)先化简,再求值:[(3m+4n)(m+2n)﹣2n(2m+4n)]÷3m,其中m=3,n=1.
【分析】原式中括号里利用多项式乘多项式,以及单项式乘多项式法则计算,去括号合并后利用多项式除以单项式法则计算得到最简结果,把m与n的值代入计算即可求出值.
【解答】解:原式=(3m2+6mn+4mn+8n2﹣4mn﹣8n2)÷3m
=(3m2+6mn)÷3m
=m+2n,
当m=3,n=1时,原式=3+2×1=3+2=5.
【点评】此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.
21.(6分)如图,已知AB∥CD,AH与BC交于点F,且点H在AD的延长线上,∠1=∠2.
(1)判断BC与DE平行吗?为什么?
(2)若∠1=110°,∠A=50°,求∠C的度数.
【分析】(1)根据对顶角相等结合题意推出∠BFD=∠2,即可判定BC∥DE;
(2)根据三角形内角和定理、平行线的性质求解即可.
【解答】解:(1)BC∥DE,理由如下:
∵∠1=∠BFD,∠1=∠2,
∴∠BFD=∠2,
∴BC∥DE;
(2)∵∠1=110°,
∴∠AFB=180°﹣∠1=70°,
∵∠A=50°,
∴∠B=180°﹣∠A﹣∠AFB=60°,
∵AB∥CD,
∴∠C=∠B=60°.
【点评】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
22.(7分)移动支付由于快捷便利已成为大家平时生活中非常普遍的支付方式.某超市除接收顾客的现金支付外,还支持“微信”“支付宝”“银行卡”“云闪付”四种支付方式,小马、小王和小张在该超市购完物后,都从“微信”、“支付宝”、“银行卡”、“云闪付”四种支付方式中随机选一种方式进行支付,每种方式被选择的可能性相同.
(1)求小马选择支付宝支付的概率;
(2)若小王选择了微信支付,求小张和小王选择同一种支付方式的概率.
【分析】(1)直接根据概率公式求解即可;
(2)若小王选择了微信支付,则小张选择支付方式有4种等可能结果,其中小张也选择微信支付的只有1种结果,再根据概率公式求解即可.
【解答】解:(1)小马选择支付宝支付的概率为;
(2)若小王选择了微信支付,则小张选择支付方式有4种等可能结果,其中小张也选择微信支付的只有1种结果,
所以小张和小王选择同一种支付方式的概率为.
【点评】本题主要考查概率公式的应用,解题的关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
23.(7分)如图为某单摆装置示意图,摆线长OA=OB=OC,当摆线位于OB位置时,过点B作BD⊥OA于点D,测得OD=15cm,当摆线位于OC位置时,OB与OC恰好垂直,求此时摆球到OA的水平距离CE的长(CE⊥OA).
【分析】利用AAS证明△COE≌△OBD,得CE=OD=15cm.
【解答】解:∵OB⊥OC,
∴∠BOD+∠COE=90°,
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,
∴∠COE=∠B,
在△COE和△OBD中,
,
∴△COE≌△OBD(AAS),
∴CE=OD=15cm,
∴摆球到OA的水平距离CE的长为15cm.
【点评】本题主要考查了全等三角形的判定与性质,证明△COE≌△OBD是解题的关键.
24.(8分)如图,在△ABC中,∠A=40°,AB=AC,点D为AC上任意一点,若△BCD是以BC为腰的等腰三角形,求∠BDC的度数.
【分析】根据等腰三角形的性质以及三角形内角和定理求出∠ABC=∠C=70°,再分两种情况进行讨论:①BC=BD;②BC=CD.
【解答】解:在△ABC中,∠A=40°,AB=AC,
∴∠ABC=∠C=(180°﹣∠A)=70°.
分两种情况:
①当BC=BD时,∠BDC=∠C=70°;
②当BC=CD时,∠BDC=∠DBC=(180°﹣∠C)=55°.
综上所述,∠BDC的度数为70°或55°.
【点评】本题考查了等腰三角形的性质,解题的关键是能够分类讨论,难度不是很大,是常考的题目之一.
25.(8分)如图,在△ABC中,AD为BC边上的高,BC=8,AD=4,点P为边BC上一动点,连接AP,随着BP长度的变化,△ACP的面积也在变化.
(1)在这个变化过程中,自变量是什么?因变量是什么?
(2)若设BP=x,△ACP的面积为y,请写出y与x的关系式;
(3)当BP=AD时,求△ACP的面积.
【分析】(1)根据函数的意义求解;
(2)根据三角形的面积公式求解;
(3)把自变量的值代入求解.
【解答】解:(1)自变量是BP长度,因变量是△ACP的面积;
(2)y=(8﹣x)×4
=﹣2x+16;
(3)当x=AD=2时,y=20,
故△ACP的面积为20.
【点评】本题考查了函数的意义,理解函数的意义是解题的关键.
26.(10分)如图,在△ABC中,∠BAC=90°,AB=AC,D为AB边的中点,BE⊥BC交CD的延长线于点E,连接AE,过点A作AF平分∠BAC交CD于点F.
(1)试判断AF与BE之间的数量关系,并说明理由;
(2)∠EAF与∠AFC互补吗?若互补,请说明理由;若不互补,请写出∠EAF与∠AFC之间的数量关系.
【分析】(1)证明△ADF≌△BDE(ASA),由全等三角形的性质得出AF=BE;
(2)证明△ABE≌△CAF(SAS),由全等三角形的性质得出∠BAE=∠ACF,由三角形内角和定理可得出结论.
【解答】解:(1)AF=BE,理由如下:
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵BE⊥BC,AF平分∠BAC,
∴∠DAF=∠CAF=∠DBE=45°,
∵D为AB的中点,
∴AD=BD,
在△ADF和△BDE中,
,
∴△ADF≌△BDE(ASA),
∴AF=BE;
(2)∠EAF与∠AFC互补.
理由如下:在△ABE和△CAF中,
,
∴△ABE≌△CAF(SAS),
∴∠BAE=∠ACF,
∵∠BAF=∠CAF=45°,
∴∠BAE+∠BAF=∠ACF+∠CAF,
即∠EAF=∠ACF+∠CAF,
∵∠ACF+∠CAF+∠AFC=180°,
∴∠EAF+∠AFC=180°,
即∠EAF与∠AFC互补.
【点评】本题考查了角平分线的定义,全等三角形的判定与性质,等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.
陕西省铜川市名校2023-2024学年八上数学期末教学质量检测模拟试题含答案: 这是一份陕西省铜川市名校2023-2024学年八上数学期末教学质量检测模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔,已知,已知,则分式的值为,等于等内容,欢迎下载使用。
2021-2022学年陕西省宝鸡市高新区七年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年陕西省宝鸡市高新区七年级(下)期末数学试卷(Word解析版),共17页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2021-2022学年陕西省铜川市新区七年级(下)期末数学试卷(Word解析版): 这是一份2021-2022学年陕西省铜川市新区七年级(下)期末数学试卷(Word解析版),共16页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。













