初中人教版第四章 几何图形初步4.1 几何图形4.1.1 立体图形与平面图形图文课件ppt

4.1　几何图形

4.1.1　立体图形与平面图形

第2课时　折叠、展开与从不同方向观察立体图形

【知识梳理】

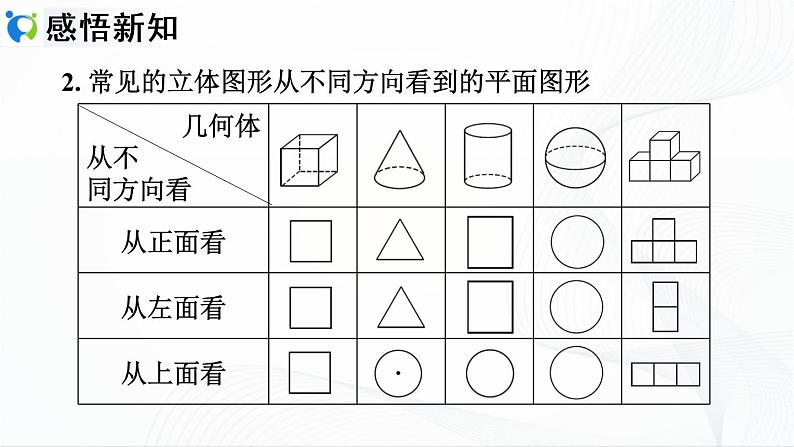
1．从      、      、      三个方向看立体图形，往往会得到不同形状的平面图形．

2．有些立体图形是由一些平面图形围成的，将它们的表面适当剪开，可以展开成平面图形．这样的平面图形称为相应立体图形的      ．

【基础强化】

知识点1　从不同方向观察立体图形

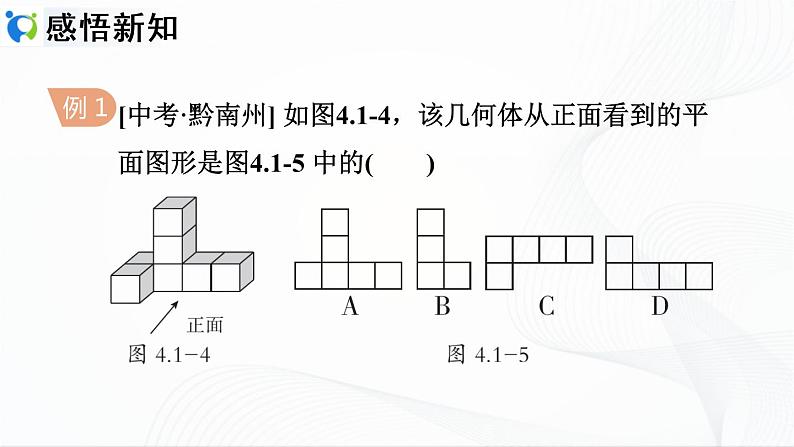
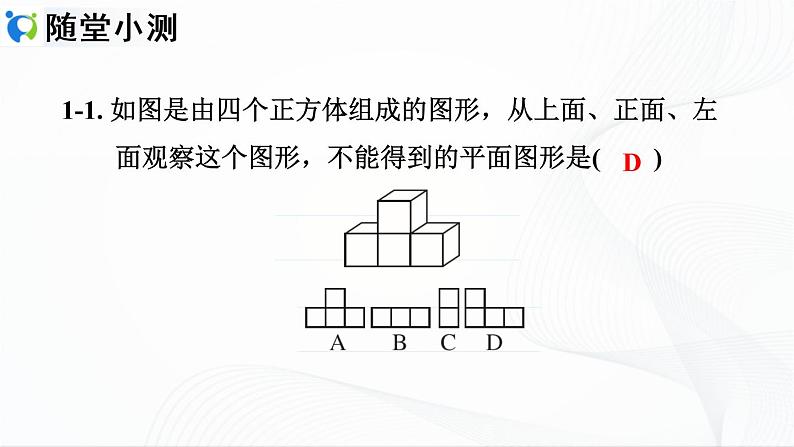
1.用3个相同的立方块搭成的几何体如图所示，则从正面看到的图形是(　　)

2.如图的几何体由5个相同的小正方体搭成.从上面看,这个几何体的形状是(      )

3.【怀柔期末】如图是一个立体图形，从左面看到的几何体的形状是(　　)

4.下列立体图形中,从正面看是四边形的有(     )

A.1个 B.2个 C.3个 D.4个

5.观察图中的几何体,图1是从　　面看到的,图2是从　　面看到的,图3是从　　面看到的. 

6.如图是由八个相同的小正方体组合而成的几何体,请分别画出从正面、左面、上面看得到的平面图形.

知识点2　立体图形的展开图

7.如图所示为几何体的平面展开图,从左到右,其对应几何体的名称分别为(      )

A.圆锥,正方体,三棱锥,圆柱

B.正方体,圆锥,四棱锥,圆柱

C.正方体,圆锥,四棱柱,圆柱

D.正方体,圆锥,圆柱,三棱柱

8.下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是(　　)

A                 B                C                 D

9.如图所示的正方体纸盒,展开后可以得到(      )

10.如图是一个几何体的表面展开图,则该几何体是　　. 

11.【黄埔区期末】如图，下列图形中，①能折叠成      ，②能折叠成      ，③能折叠成      ．

【知能提升】

一、选择题

1.如图的两个圆柱体底面半径相同而高度不同，关于从不同的方向看这两个圆柱体得到的平面图形，下列说法中正确的是(    )

A.从正面看得到的平面图形相同    B．从上面看得到的平面图形相同

C．从左面看得到的平面图形相同   D．从各个方向看得到的平面图形都相同

2.下列图形中,是棱柱表面展开图的是(      )

3.【光明区期末】将圆锥如图放置，现用一个平面截去它的上半部分，则从正面看下半部分的几何体可能的图形是（    ）

4.如图，从上面看该几何体得到的图形是 (　　)

A             B             C               D

5.把如图中的三棱柱展开，所得到的展开图是（    ）

6.如图,BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是(      )

7.如图是由一些大小相同的小正方体组成的几何体从三个方向看得到的图形,那么组成这个几何体的小正方体的个数为(      )

A.8  B.7  C.6  D.5

8.如图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是(      )

A.正方体 B.球 C.圆锥 D.圆柱体

9.【无锡中考】如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开(外表面朝上)，展开图可能是(　　)

10.湖南省第二次文物普查时，省考古研究所在冷水滩钱家州征集到一个宋代的“青釉瓜棱形瓷执壶”，如图所示，该壶为盛酒器．该“青釉瓜棱形瓷执壶”从正面看到的平面图形是(　　)

A           B        C        D

二、填空题

11.如图是由若干个小正方体组成的几何体,其中阴影部分是空缺的通道,一直通到对面,则这个立体图形由　　个小正方体组成. 

第11题图              第12题图                               第13题图

12.如图是六个棱长为1的正方体组成的一个几何体,则从上面看到的平面图形的面积是　　. 

13.【攀枝花中考】如图是一个多面体的表面展开图，如果面F在前面，从左面看是面B，那么从上面看是面    .(填字母)

14.【武侯区期中】如图所示的长方形是圆柱的侧面展开图，已知这个长方形相邻的两边长分别为6，4π，则圆柱体的体积为      .

三、解答题

15.如图是长方体的平面展开图,每个面都标注有字母.请回答下列问题:

(1)该长方体中,哪些面是相对的?

(2)如果C在左面,D在上面,则其他各个面应在什么位置?

(3)如果该长方体中,相对的两个面上的字母表示的数互为相反数,且A＝2,B＝0,C＝－1,求D,E,F的值.

16.如图是一个长方体的展开图，每一面都标注了字母(标字母的面是外表面)，根据要求回答问题：

(1)如果D面在多面体的左面，那么F面在哪一方？

(2)B面和哪个面是相对的面？

(3)如果C面在前面，从上面看到的是D面，那么从左面看是哪个面？

(4)如果B面在后面，从左面看是D面，那么前面是哪个面？

(5)如果A面在右面，从下面看是F面，那么B面在哪一方？

17.用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?

(1)它最多需要多少个小正方体?

(2)它最少需要多少个小正方体?

18.如图是一个食品包装盒的表面展开图，其底面为正六边形．(其中a＝8 cm，b＝2 cm)

(1)请写出这个包装盒对应的多面体的名称；

(2)请根据图中所标的尺寸，计算这个多面体的侧面积．

19.由几个相同的边长为1的小立方块搭成的几何体从上面看得到的图形如图所示,格中的数字表示该位置上小立方块的个数.

(1)请在下面方格纸中分别画出这个几何体从正面、左面看得到的图形;

(2)这个几何体的表面积为　　个平方单位;(包括底面积) 

(3)若上述小立方块搭成的几何体从上面看得到的图形不变,各位置上小立方块的个数可以改变(总数目不变),则搭成这样的组合几何体的所有情况中,表面积最大的是　　个平方单位.(包括底面积) 

参考答案

【知识梳理】

1．从正面、左面、上面三个方向看立体图形，往往会得到不同形状的平面图形．

2．有些立体图形是由一些平面图形围成的，将它们的表面适当剪开，可以展开成平面图形．这样的平面图形称为相应立体图形的展开图．

【基础强化】

知识点1　从不同方向观察立体图形

1.用3个相同的立方块搭成的几何体如图所示，则从正面看到的图形是(　A　)

2.如图的几何体由5个相同的小正方体搭成.从上面看,这个几何体的形状是(   D   )

3.【怀柔期末】如图是一个立体图形，从左面看到的几何体的形状是(　A　)

4.下列立体图形中,从正面看是四边形的有(   B   )

A.1个 B.2个 C.3个 D.4个

5.观察图中的几何体,图1是从　上　面看到的,图2是从　正　面看到的,图3是从　左　面看到的. 

6.如图是由八个相同的小正方体组合而成的几何体,请分别画出从正面、左面、上面看得到的平面图形.

略

知识点2　立体图形的展开图

7.如图所示为几何体的平面展开图,从左到右,其对应几何体的名称分别为(   D   )

A.圆锥,正方体,三棱锥,圆柱

B.正方体,圆锥,四棱锥,圆柱

C.正方体,圆锥,四棱柱,圆柱

D.正方体,圆锥,圆柱,三棱柱

8.下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是(　C　)

A                 B                C                 D

9.如图所示的正方体纸盒,展开后可以得到(   A   )

10.如图是一个几何体的表面展开图,则该几何体是　三棱柱　. 

11.【黄埔区期末】如图，下列图形中，①能折叠成圆柱，②能折叠成五棱柱，③能折叠成圆锥．

【知能提升】

一、选择题

1.如图的两个圆柱体底面半径相同而高度不同，关于从不同的方向看这两个圆柱体得到的平面图形，下列说法中正确的是(  B  )

A.从正面看得到的平面图形相同    B．从上面看得到的平面图形相同

C．从左面看得到的平面图形相同   D．从各个方向看得到的平面图形都相同

2.下列图形中,是棱柱表面展开图的是(   C   )

3.【光明区期末】将圆锥如图放置，现用一个平面截去它的上半部分，则从正面看下半部分的几何体可能的图形是（  A  ）

4.如图，从上面看该几何体得到的图形是 (　A　)

A             B             C               D

5.把如图中的三棱柱展开，所得到的展开图是（  B  ）

6.如图,BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是(   A   )

7.如图是由一些大小相同的小正方体组成的几何体从三个方向看得到的图形,那么组成这个几何体的小正方体的个数为(   C   )

A.8  B.7  C.6  D.5

8.如图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是(   D   )

A.正方体 B.球 C.圆锥 D.圆柱体

9.【无锡中考】如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开(外表面朝上)，展开图可能是(　D　)

10.湖南省第二次文物普查时，省考古研究所在冷水滩钱家州征集到一个宋代的“青釉瓜棱形瓷执壶”，如图所示，该壶为盛酒器．该“青釉瓜棱形瓷执壶”从正面看到的平面图形是(　D　)

A           B        C        D

二、填空题

11.如图是由若干个小正方体组成的几何体,其中阴影部分是空缺的通道,一直通到对面,则这个立体图形由　38　个小正方体组成. 

第11题图              第12题图                               第13题图

12.如图是六个棱长为1的正方体组成的一个几何体,则从上面看到的平面图形的面积是　5　. 

13.【攀枝花中考】如图是一个多面体的表面展开图，如果面F在前面，从左面看是面B，那么从上面看是面  C  .(填字母)

14.【武侯区期中】如图所示的长方形是圆柱的侧面展开图，已知这个长方形相邻的两边长分别为6，4π，则圆柱体的体积为24π或36.

【解析】①以4π为底面周长，6为高，此时圆柱体的底面半径为＝2，所以圆柱体的体积为π×22×6＝24π；②以6为圆柱体的底面周长，4π为高，此时圆柱体的底面半径为＝，所以圆柱体的体积为π×2×4π＝36.

三、解答题

15.如图是长方体的平面展开图,每个面都标注有字母.请回答下列问题:

(1)该长方体中,哪些面是相对的?

(2)如果C在左面,D在上面,则其他各个面应在什么位置?

(3)如果该长方体中,相对的两个面上的字母表示的数互为相反数,且A＝2,B＝0,C＝－1,求D,E,F的值.

解:(1)A与D,B与F,C与E是相对的.

(2)根据C在左面,D在上面,所以E在右面,A在下面,B在后面,F在前面.

(3)因为A＝2,B＝0,C＝－1,所以D＝－2,E＝1,F＝0.

16.如图是一个长方体的展开图，每一面都标注了字母(标字母的面是外表面)，根据要求回答问题：

(1)如果D面在多面体的左面，那么F面在哪一方？

(2)B面和哪个面是相对的面？

(3)如果C面在前面，从上面看到的是D面，那么从左面看是哪个面？

(4)如果B面在后面，从左面看是D面，那么前面是哪个面？

(5)如果A面在右面，从下面看是F面，那么B面在哪一方？

解：(1)右方　(2)E面　(3)B面

(4)E面　(5)后方

17.用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.这样的几何体只有一种吗?

(1)它最多需要多少个小正方体?

(2)它最少需要多少个小正方体?

解:这样的几何体不止一种.

(1)最多需要3＋9＋2＝14(个).

(2)最少需要3＋5＋2＝10(个).

18.如图是一个食品包装盒的表面展开图，其底面为正六边形．(其中a＝8 cm，b＝2 cm)

(1)请写出这个包装盒对应的多面体的名称；

(2)请根据图中所标的尺寸，计算这个多面体的侧面积．

解：(1)六棱柱　

(2)侧面积是6个长方形的面积之和，则这个多面体的侧面积为6ab＝6×8×2＝96(cm2)

19.由几个相同的边长为1的小立方块搭成的几何体从上面看得到的图形如图所示,格中的数字表示该位置上小立方块的个数.

(1)请在下面方格纸中分别画出这个几何体从正面、左面看得到的图形;

(2)这个几何体的表面积为　24　个平方单位;(包括底面积) 

(3)若上述小立方块搭成的几何体从上面看得到的图形不变,各位置上小立方块的个数可以改变(总数目不变),则搭成这样的组合几何体的所有情况中,表面积最大的是　26　个平方单位.(包括底面积) 

解:(1)图略.

(3)提示:要使表面积最大,则需满足两正方体重合得最少,此时从上面看得到的图形如图,表面积为26.