初中数学湘教版七年级上册第2章 代数式综合与测试单元测试课时作业

湘教版初中数学七年级上册第二章《代数式》单元测试卷

考试范围：第二章；考试时间：120分钟；总分：120分

学校:___________姓名：___________班级：___________考号：___________

第I卷（选择题）

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. 一个两位数和一个三位数，若将两位数放在三位数的左边组成一个五位数，则组成的这个五位数表示为(    )

A.  B.  C.  D.

2. 有米长的木料，要做成一个窗框如图如果假设窗框横档的长度为米，那么窗框的面积是(    )

A. 米 B. 米
C. 米 D.   米

3. 某商店经销一批衬衣，每件进价为元，零售价比进价高，后因市场变化，该商店把零售价调整为原来零售价的出售．那么调整后每件衬衣的零售价是(    )

A. 元 B. 元
C. 元 D. 元

4. 观察下列树枝分叉的规律图，若第个图树枝数用表示，则的值为．(    )

A.  B.  C.  D.

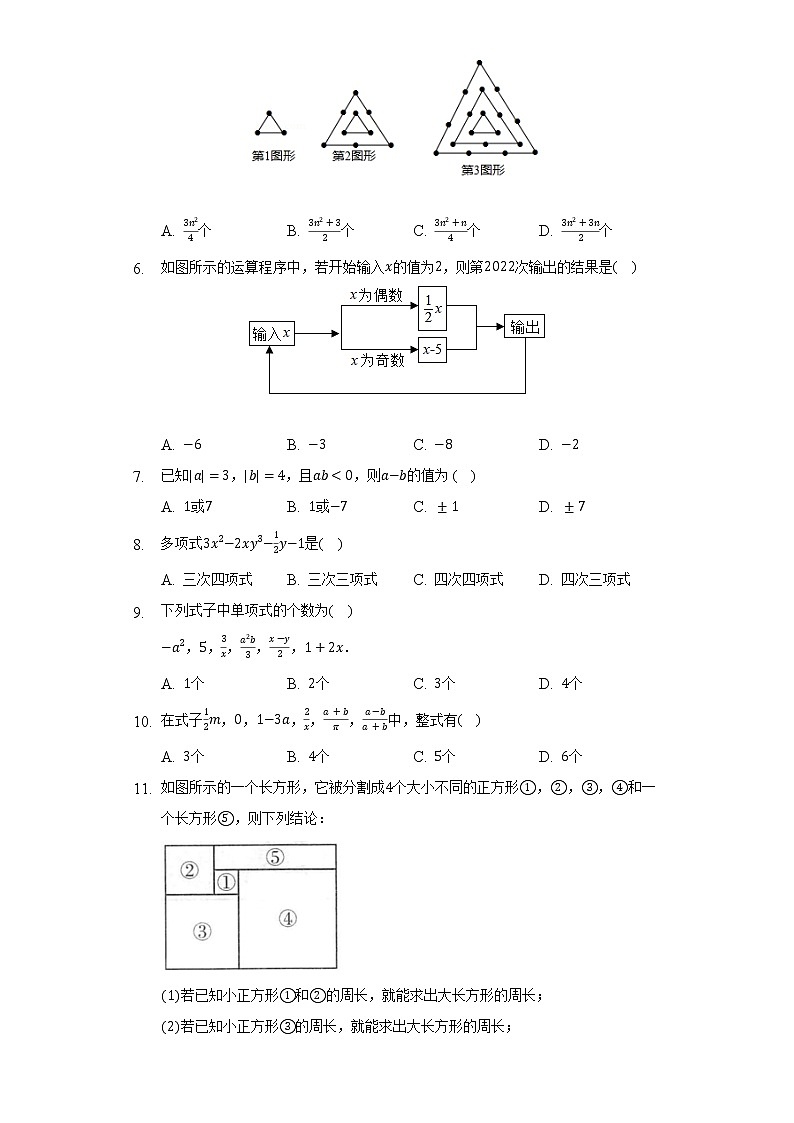
5. 观察如图图形，它们是按一定规律排列的，依照此规律，第个图形中的小点一共有(    )

A. 个 B. 个 C. 个 D. 个

6. 如图所示的运算程序中，若开始输入的值为，则第次输出的结果是(    )

A.  B.  C.  D.

7. 已知，，且，则的值为(    )

A. 或 B. 或 C.  D.

8. 多项式是(    )

A. 三次四项式 B. 三次三项式 C. 四次四项式 D. 四次三项式

9. 下列式子中单项式的个数为(    )
   ，，，，，．

A. 个 B. 个 C. 个 D. 个

10. 在式子，，，，，中，整式有(    )

A. 个 B. 个 C. 个 D. 个

11. 如图所示的一个长方形，它被分割成个大小不同的正方形，，，和一个长方形，则下列结论：
    
    若已知小正方形和的周长，就能求出大长方形的周长；
    若已知小正方形的周长，就能求出大长方形的周长；
    若已知小正方形的周长，就能求出大长方形的周长；
    若已知小长方形的周长，就能求出大长方形的周长；
    其中正确的是(    )

A.  B.  C.  D.

12. 三张大小不一的正方形纸片按如图和图方式分别放置于相同的长方形中，它们既不重叠也无空隙，记图阴影部分周长之和为，图阴影部分周长为，要求与的差，只需知道一个图形的周长，这个图形是(    )

A. 整个长方形 B. 图正方形 C. 图正方形 D. 图正方形

第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）

13. 某企业今年月份产值为万元，月份比月份减少了，月份比月份增加了，则月份的产值是____________万元．
14. 已知，则______．
15. 有一个只含字母的二次三项式，其二次项系数为，一次项系数为，常数项为，则这个二次三项式是________．
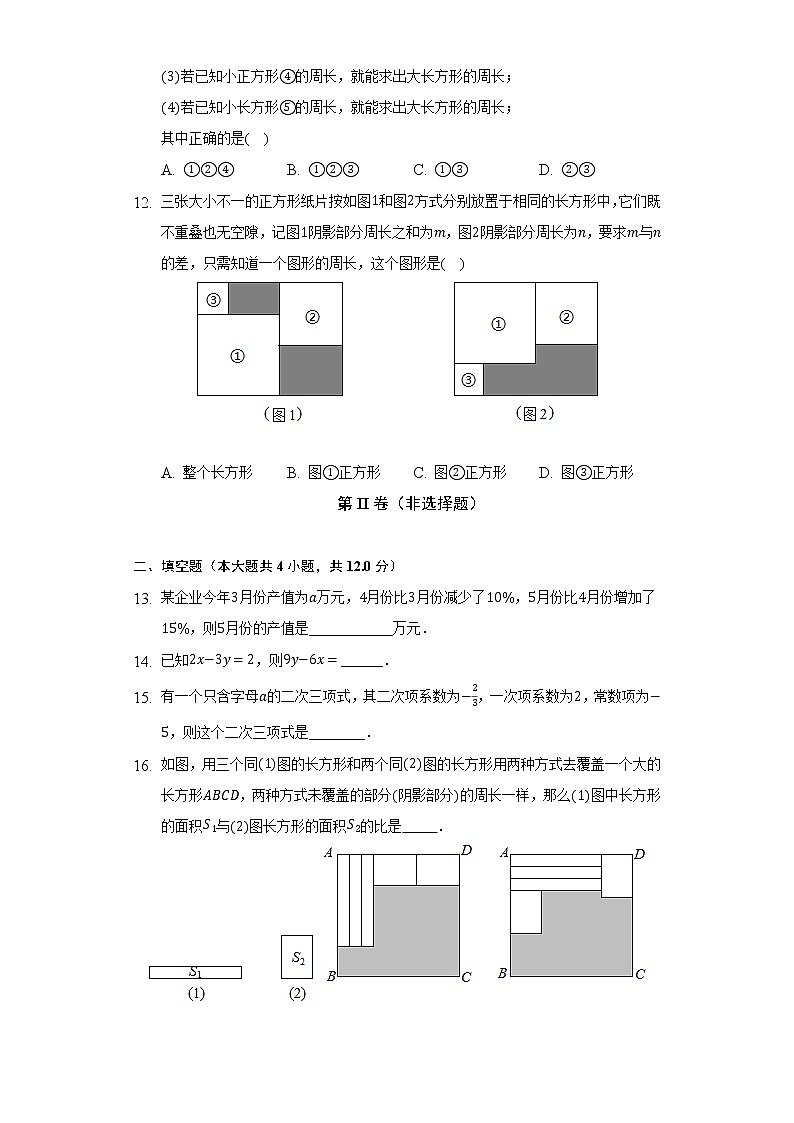
16. 如图，用三个同图的长方形和两个同图的长方形用两种方式去覆盖一个大的长方形，两种方式未覆盖的部分阴影部分的周长一样，那么图中长方形的面积与图长方形的面积的比是          ．

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

17. 某商场销售一种西装和领带，西装每套定价元，领带每条定价元国庆节期间商场决定开展促销活动活动期间向客户提供两种优惠方案：
    方案一：买一套西装送一条领带；
    方案二：西装和领带都按定价的付款；
    现某客户要到该商场购买西装套，领带条．
    若该客户按方案一购买，需付款多少元用含的式子表示若该客户按方案二购买，需付款多少元用含的式子表示
    若，通过计算说明此时按哪种方案购买较为合算
    当时，你能给出一种更为省钱的购买方案吗试写出你的购买方法和所需费用．
18. 如图所示是一个长为，宽为的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图的方式拼成一个正方形．

图中的大正方形的边长为_____；阴影部分的正方形的边长为_____；

请用两种方式表示图中阴影部分的面积；

19. 数轴上有两个动点，，如果点始终在点的左侧，我们称作点是点的“追赶点”。如图，数轴上有个点，，它们表示的数分别为，，已知点是点的“追赶点”，且，表示的数分别为，．
    
    由题意易知，点是点的“追赶点”，表示线段的长，以下相同；类似的，______．
    在，，三点中，若其中一个点是另两个点所构成线段的中点，请用含的代数式来表示．
    若，，求和的值．
20. 某校为了丰富学生的课余生活：计划购买一些乒乓球拍和乒乓球，已知一副乒乓球拍的标价为元，一盒乒乓球的标价是元．现了解到两家文具店都在做促销活动，甲文具店：买一副乒乓球拍送一盒乒乓球；乙文具店：所有商品均打八折，若学校计划购买乒乓球拍副，乒乓球盒．
    用含的代数式分别表示在甲、乙两家文具店购买球拍和球的总费用；
    若学校计划购买乒乓球盒，选择在甲、乙其中一家文具店购买，请问在哪家购买合算；
    在的条件下，若还可以选择在甲、乙两家文具店同时购买，请你设计种最省钱的购买方案．
21. 如图，长为，宽为的大长方形被分割为小块，除阴影 ，外，其余块是形状、大小完全相同的小长方形，其较短一边长为 ．
    从图可知，每个小长方形较长的一边长是______ 用含的代数式表示．
    分别用含，的代数式表示阴影，的面积，并计算阴影，的面积差．
    当时，阴影与阴影的面积差会随着的变化而变化吗？请你作出判断，并说明理由．

22. 某商场销售一种西装和领带，西装每套定价元，领带每条定价元，“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案现某客户要到商场购买西装套，领带条．
    方案一：买一套西装送一条领带
    方案二：西装和领带都按定价的付款．
    若客户按方案一购买，则需付款          元
    若客户按方案二购买，则需付款          元
    若，请通过计算说明此时按哪种方案购买较为合算
    当时，你能给出一种更为省钱的购买方案吗试写出你的购买方案，并计算此方案需要付款多少元．
23. 试说明代数式的值与的值无关．
24. 按照规律填上所缺的单项式，并回答问题：

，，，，________，________；

试写出第个和第个单项式；

试写出第为正整数个单项式；

试计算：当时，的值．

25. 某市居民使用自来水按如下标准收费水费按月缴纳：

当时，某用户一个月用了水，求该用户这个月应缴纳的水费．

设某户月用水量为立方米，当时，则该用户应缴纳的水费_____元用含、的整式表示．

当时，甲、乙两用户一个月共用水，已知甲用户缴纳的水费超过了元，设甲用户这个月用水，试求甲、乙两用户一个月共缴纳的水费用含的整式表示．

答案和解析

1.【答案】 

【解析】

【分析】
此题考查列代数式，注意数位对应的计数单位是解决问题的关键．
是一个两位数，是一个三位数，把放在的左边构成一个五位数，可以看做位于千位上，位于个位上，所以这个五位数的表达式是．
【解答】
解：根据题意得，这个五位数的表达式是．
 故选D  

2.【答案】 

【解析】

【分析】

本题主要考查列代数式，解决问题的关键是读懂题意，找到所求的量的等量关系，需注意，用字母表示数时，数字通常写在字母的前面，带分数的要写成假分数的形式．
横档的长度为米，则竖档的长度，根据窗框的面积长宽求出答案．
【解答】
解：竖档的长度，
窗框的面积长宽
故选：．

3.【答案】 

【解析】

【分析】
本题考查了列代数式，由题意利用得到的等量关系式：零售价进价，调价后的价格零售价，把相关数值代入即可求解． 
【解析】
解：根据题意，这批衬衣的零售价为每件元，因调整后的零售价为原零售价的，所以调价后每件衬衣的零售价为元．故选B．  

4.【答案】 

【解析】

【分析】
本题考查了图形变化类的规律问题，根据图形可知每一个树枝上长着两个小树枝是本题的关键．
根据已知图中规律可得：，相减可得结论．
【解答】 
解：由题意得：
第个图：，
第个图：，
第个图：，
第个图：，

第个图：，
．  

5.【答案】 

【解析】

【分析】
本题考查了图形的变化类问题，解题的关键是能够找到图形的变化规律，然后求解．由已知图形得出点的个数是从到序数连续整数和的倍，据此可得答案．
【解答】
解：第个图形有个点，
第个图形有个点
第个图形有个点；

第个图形有个点，
故选：．  

6.【答案】 

【解析】

【分析】
本题考查数字的变化规律，能够通过所给条件，探索出输出数的规律是解题的关键．
分别求出第次，第次，第次，第次，第次，第次，第次的结果，从第次开始，结果开始循环，每输入次结果循环一次；所以第次输出的结果与第次输出的结果相同，即可求解．
【解答】
解：当时，输出为，
当时，输出为，
当时，输出为，
当时，输出为，
当时，输出为，
当时，输出结果为，
当时，输出为；
当时，输出为；

由此可知，从第次开始，输出的结果是以，，，，，循环往复的，
因为
第次输出结果和第次结果相同，即为．
故选：．  

7.【答案】 

【解析】

【分析】
本题主要考查的是有理数的减法、绝对值、有理数的乘法，求得当时，；当时，是解题的关键．由绝对值的性质可知，，由可知、异号，从而判断出、的值，最后代入计算即可．
【解答】

解：，，
，．
，
当时，；当时，．
当，时，原式；
当，时，原式．
故选D．

8.【答案】 

【解析】解：多项式的最高次项的次数为，共有项，故此该多项式为四次四项式．
故选：．
依据多项式的项、多项式的次数的概念回答即可．
本题主要考查的是多项式的概念，掌握多项式的概念是解题的关键．
 

9.【答案】 

【解析】

【分析】
本题主要考查的是单项式、多项式、分式的定义有关知识，根据单项式、多项式、分式的定义回答即可．
【解答】
解：是单项式；单独一个数字是单项式，故是单项式；是分式；是单项式；是多项式；是多项式．
故选C．  

10.【答案】 

【解析】

【分析】
本题重点对整式定义的考查：整式是有理式的一部分，在有理式中可以包含加，减，乘，除四种运算，但在整式中除数不能含有字母．
单项式和多项式统称为整式．
根据整式的定义进行解答即可．
【解答】
解：和分母中含有未知数，则不是整式，其余的都是整式共四个．
故选B．  

11.【答案】 

【解析】

【分析】
本题考查了整式的加减，长方形、正方形的性质以及周长等知识，解题的关键是学会利用参数解决问题．记正方形的边长分别为、、、用含、的代数式表示出大长方形的周长，即可判断正确；用含的代数式表示出大长方形的周长，即可判断正确；不能只用含的代数式表示出大长方形的周长，即可判断错误；用含的代数式表示出长方形的周长，结合，得出大长方形的周长小长方形的周长，即可判断正确．
【解答】
解：设正方形的边长分别为、、、．
大长方形的周长，
因为，所以，，
所以大长方形的周长，
故正确；
大长方形的周长，
因为，所以，
所以大长方形的周长，
故正确；
由可知，大长方形的周长，
而，所以，
所以已知小正方形与的周长，才能求出大长方形的周长，
故错误；
由可知，大长方形的周长．
长方形的周长，
因为，
所以长方形的周长．
所以大长方形的周长小长方形的周长，
故正确．
故选：．  

12.【答案】 

【解析】解：设正方形的边长为、正方形的边长为、正方形的边长为，可得

   
   
   ，

 
 
  ，
所以

，
故选：．
设正方形的边长为、正方形的边长为、正方形的边长为，分别表示出、的值，就可计算出的值为，从而可得只需知道正方形的周长即可．
该题考查了数形结合解决问题的能力，关键是能根据图形正确列出算式并计算．
 

13.【答案】万元 

【解析】

【分析】

此题考查了列代数式，理解各月之间的百分比的关系是解题的关键，根据月份、月份与月份的产值的百分比的关系列式计算即可得解．

【解答】

解：月份的产值为：万元 
故答案为万元．

14.【答案】 

【解析】解：，
，
故答案为：．
通过观察可知：，再把代入即可．
本题考查了代数式求值，关键在于学生要将进行变形，再将代入即可．
 

15.【答案】 

【解析】

【分析】
此题考查的是多项式的定义，根据条件及多项式的项及次数的定义可以得出所求的多项式此题已知是只含字母的二次三项式，而且系数、常数项都知道，因此可得这个多项式．
【解答】
解：由题意得，该多项式为．
故答案为．  

16.【答案】： 

【解析】

【分析】
本题考查的是整式的加减，列代数式有关知识，本题需先设图中长方形的长为，宽为，图中长方形的宽为，长为，再结合图形分别得出图形的阴影周长和图形的阴影周长，相等后列等式可得：，，最后根据长方形面积公式可得结论．
【解答】
解：设图中长方形的长为，宽为，
图中长方形的宽为，长为，
由两个长方形的，
图阴影部分周长为：
，
图阴影部分周长为：
，

两种方式未覆盖的部分阴影部分的周长一样，
，
即，
，
，
．
故答案为：．  

17.【答案】解：方案一购买，需付款：元，
按方案二购买，需付款：元；
把分别代入：元，
元．
因为，所以按方案一购买更合算；
先按方案一购买套西装送条领带，再按方案二购买条领带，共需费用：
，
当时，元． 

【解析】本题考查了用字母表示数的相关的题目．
根据题目提供的两种不同的付款方式列式即可；
将分别代入求得的式子中即可得到方案一和二的费用，然后比较即可得到选择哪种方案更合算；
根据题意考虑可以先按方案一购买套西装获赠送条领带，再按方案二购买条领带更合算．
 

18.【答案】，；

解：图中阴影部分的面积一是看作正方形的面积则为：，

也可看作是大正方形的面积减去四个小长方形的面积：表示为．

【解析】

【分析】

本题考查的是列代数式，矩形的性质有关知识．

根据图形直接写出大正方形的边长和阴影部分正方形的边长即可；

利用面积法直接表示出答案即可．

【解答】

解：图中的大正方形的边长为：；阴影部分的正方形的边长为：；

故答案为，．

见答案．

19.【答案】
是、的中点，
；
是、点中点时，；
是、的中点时，
；
，
，
，
，
或
或或，
，或，或，或，，
，
，或，或，． 

【解析】

【分析】
本题考查了列代数式，一元一次方程的应用以及数轴上两点间的距离公式，解题的关键是：根据两点间的距离公式求出线段的长；根据数量关系表示出的长度；根据数量关系表示出的长度．本题属于基础题，难度不大，解决该题型题目时，结合数量关系表示出线段的长度，再根据线段间的关系列出方程是关键．
由两点间距离直接求解；
是、的中点，；当点在、点中点时，；是、的中点时，；
由已知可得，，分情况求解即可．
【解答】
解：，
故答案为；
见答案；
见答案．  

20.【答案】解：甲店购买需付款元；
乙店购买需付款元；
当时，
甲店需元；
乙店需元；

在乙店购买合算；
先在甲店购买副球拍，送盒乒乓球需元，另外盒乒乓球在乙店购买需元，共需元． 

【解析】按照对应的方案的计算方法分别列出代数式即可；
把代入求得的代数式求得数值，进一步比较得出答案即可；
根据两种方案的优惠方式，可得出先在甲店购买副球拍，送盒乒乓球，另外盒乒乓球在乙店购买即可．
此题考查列代数式，理解两种方案的优惠方案，得出运算的方法是解决问题的关键．
 

21.【答案】 

【解析】解：由于大长方形的长为，
每个小长方形的短边都为，
故每个小长方形的较长边为：
阴影 的面积：         ；
阴影 的面积：         ．
阴影 的面积与阴影 的面积差      
当 时，，
故阴影 ，的面积差不会改变．
故答案为：
根据图形即可取出答案．
分别求出阴影、的面积即可求出答案．
将代入中即可求出答案．
本题考查整式的运算，解题的关键是根据题意列出式子，本题属于中等题型
 

22.【答案】解：．
当时，
方案一费用：元，
方案二费用：元
，按方案一购买较合算．
能先按方案一购买套西装获赠条领带，再按方案二购买条领带元．
故此方案需要付款元． 

【解析】见答案
 

23.【答案】解：


的值与的值无关． 

【解析】本题须先根据整式的混合运算对代数式进行化简，最后即可得出代数式的值与的值无关．
本题主要考查了整式的混合运算，在解题时要注意混合运算的顺序．
 

24.【答案】解： 

第个单项式为，第个单项式为．

第个单项式为．

原式．

【解析】见答案
 

25.【答案】解：

元
答：该用户这个月应缴纳元水费．

甲用户缴纳的水费超过了元，


甲：，
乙：，
，
共计：；

甲：，
乙：

共计：；

甲：，
乙：
，
共计：．
故甲、乙两用户共缴纳的水费：
当 时，缴水费元；
当时，缴水费元；
当时，缴水费元． 

【解析】

【分析】
本题考查了整式的加减、列代数式等知识点．题目难度中等，针对不同情况分类讨论是解决的关键．
根据用户用水情况，根据不同单价计算其应缴纳的水费；
根据用水量，代入不同的单价，计算出应缴纳的水费；
先判断甲户的用水量大致范围，再分类进行讨论计算．
【解析】
见答案


元
故答案为：
见答案