初中数学北师大版九年级下册2 二次函数的图像与性质集体备课课件ppt

这是一份初中数学北师大版九年级下册2 二次函数的图像与性质集体备课课件ppt，共31页。PPT课件主要包含了向上平移3个单位，向下平移2个单位，左右平移规律，yax-h2，yax+h2，yax2，要点归纳，直线xh，跟踪训练，归纳升华等内容，欢迎下载使用。

1.说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
(1)y=ax2(2)y=ax2+c
1.二次函数 y=ax2+c与y=ax2的图象有何关系？
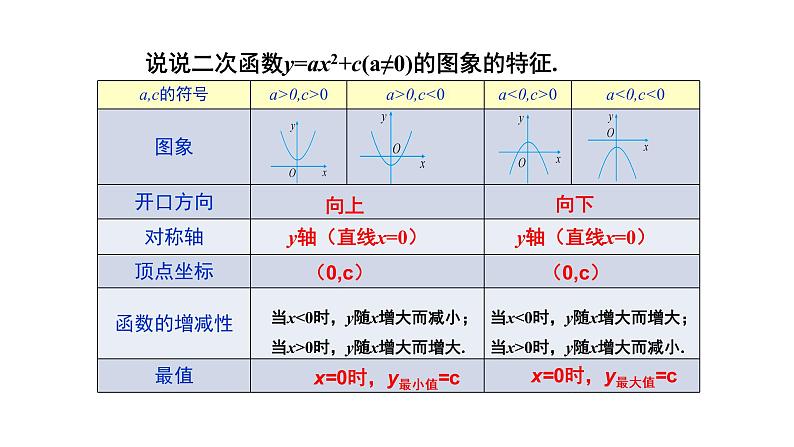
二次函数y=ax2+c的图象可以由 y=ax2的 图象平移得到： 当c > 0 时，向上平移|c |个单位长度得到. 当c < 0 时，向下平移|c |个单位长度得到.
2.请说出二次函数y=-2x2的开口方向、顶点坐标、对称轴及最值？
3.把y=-2x2的图象
4.二次函数y=-5x2+3的图象如何平移得到y=-5x2的图象？
本质：上下平移，改变了函数的顶点坐标，不改变函数的对称轴。
当x<0时，y随x增大而减小；当x>0时，y随x增大而增大.
当x<0时，y随x增大而增大；当x>0时，y随x增大而减小.
x=0时，y最小值=c
x=0时，y最大值=c
说说二次函数y=ax2+c(a≠0)的图象的特征.
1.函数 的图象的顶点坐标是 ；开口方向是 ；最 值是 .2.函数y=-2x2+3的图象可由函数 的图象向 平移 个单位得到.3.把函数y=-3x2的图象向下平移2个单位可得到函数__________的图象.
1.经历探索二次函数y=ax2+bx+c的图象的作法和性质的过程.2.体会建立二次函数对称轴和顶点坐标公式的必要性.3.能够作出y=a（x-h）2和y=a（x-h）2+k的图象，并能理解它与y=ax2的图象的关系.理解a，h和k对二次函数图象的影响.4.能够正确说出y=a（x-h）2+k的图象的开口方向、对称轴和顶点坐标.
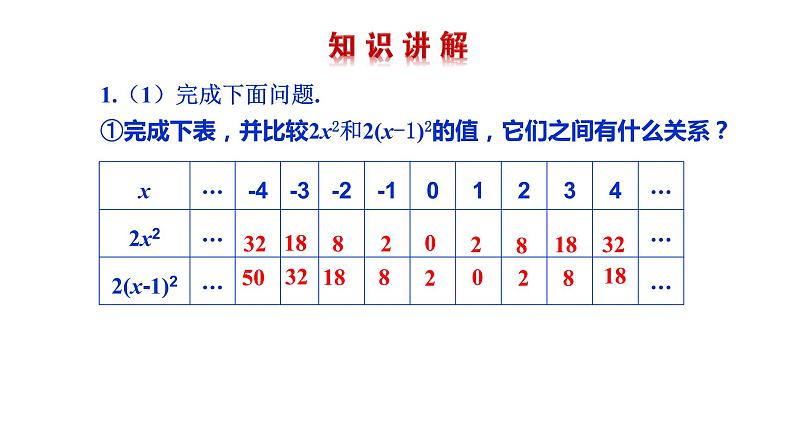
1.（1）完成下面问题.①完成下表，并比较2x2和2(x-1)2的值，它们之间有什么关系？
②在下图中作出二次函数y=2(x-1)2的图象
③函数y=2(x-1)2的图象与y=2x2的图象有什么关系？它是轴对称图形吗？它的对称轴和顶点坐标分别是什么？
函数y=2(x-1)2的图象由y=2x2的图象向右平移1个单位得到，它是轴对称图形.对称轴：直线x=1顶点坐标：（1，0）
类似地，你能发现二次函数y=2（x+1）2的图像与二次函数y=2x2的图像有什么关系吗？
二次函数y=a（x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到(h>0).
当向左平移 ︱h︱ 时
当向右平移 ︱h︱ 时
本质：左右平移，改变了函数的对称轴位置，不改变函数的最值。
括号内左加右减；括号外不变.
④对于函数y=2(x-1)2和y=2(x+1)2，x取哪些值时， y值随x值的增大而增大？ x取哪些值时， y值随x值的增大而减小？
函数y=2(x-1)2(y=2x2或y=2(x+1)2) 当x>1 (x>0 或 x>-1)时， y值随x值的增大而增大; 当x<1 (x<0 或 x<-1)时， y值随x值的增大而减小.
基础函数y=2x2的所有与范围和位置有关的性质全部作对应的平移即可得到平移函数的对应的性质
二次函数 y=a(x-h)2的性质
当x=h时，y最小值=0
当x=h时，y最大值=0
当x＜h时，y随x的增大而减小；x＞h时，y随x的增大而增大.
当x＞h时，y随x的增大而减小；x＜h时，y随x的增大而增大.
在同一坐标系中画出下列函数的图象：
思考：它们的图象之间有什么关系？
函数 的图象
函数y=a(x-h)2的图象
对称轴是 直线x=h ；
函数 的图象
函数y=a(x-h)2的图象：
函数y=ax2与y=a(x-h)2的图象关系：
画出二次函数y=3(x-1)2+2的图象，并与二次函数y=3x2的图象进行比较，说明它们之间的关系.
函数 的图象
函数 的图象
（当k,h都大于0时）的图象特点.
二次函数y=a(x-h)2+k的图象和性质
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
平移规律：括号内：左加右减；括号外不变.
探索y=a(x-h)2的图象及性质
a>0,开口向上a<0,开口向下a的符号决定增减性
1.（无锡·中考）下列二次函数中，图象以直线x=2为对称轴、且经过点(0，1)的是( )(x－2)2+1 B.y=(x+2)2+1 C.y=(x－2)2－3 D.y=(x+2)2－3【解析】根据以直线x=2为对称轴可知选项A，C符合，再根据图象经过点(0，1)知选项C符合.
2．（西宁·中考）将抛物线
向左平移1个单位后所得到的新抛物线的表达式为__________.
3．（襄樊·中考）将抛物线 先向上平移2个单位，再向右平移1个单位后，得到的抛物线的表达式为________________________________________．