人教版九年级数学上册 二次函数复习与总结课件

这是一份人教版九年级数学上册 二次函数复习与总结课件，共15页。PPT课件主要包含了二次函数的特殊形式，1a的符号，开口向上，开口向下，2C的符号，交点在x轴上方，交点在x轴下方，经过坐标原点，3b的符号，由对称轴的位置确定等内容，欢迎下载使用。

知识点一 二次函数的定义
一般地，如果y=ax2+bx+c (a,b,c是常数，a≠0),那么y叫做x的二次函数.
注意：二次项系数a≠0；自变量x的最高次数是2.
思考：常数b和c可以为0吗？
其中二次项为ax2，一次项为bx，常数项c
二次项的系数为a，一次项的系数为b，常数项c
知识点二：二次函数的表达式:
二次函数的一般式：y=ax2+bx+c (其中a、b、c是常数,a≠0)
当b=0时， y=ax2+c当c=0时， y=ax2+bx当b=0，c=0时， y=ax2
2.二次函数顶点式： y=a（x-h)2+k（a≠0）。3.二次函数的交点式：y=a（x-x1)(x-x2)（a≠0)。
问题2：描点法画函数图象的一般步骤是哪些？
1.列---列表（表中给出一些自变量的值及其对应的函数值）； 2.描---描点（在直角坐标系中描出表中数值对应的各点）； 3.连---连线（按照横坐标由小到大的顺序把所描各点用平滑的曲线连接起来）.
问题1：一般用什么方法画函数的图象？
知识点三 二次函数的图象和性质
二次函数 y= ax2+bx+c (a≠0) 的图象和性质
y= ax2+bx+c (a>0)
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
y= ax2+bx+c (a<0)
a 的值越大时，开口越小，y 变化越快
a 的值越小时，开口越大， y 变化越慢
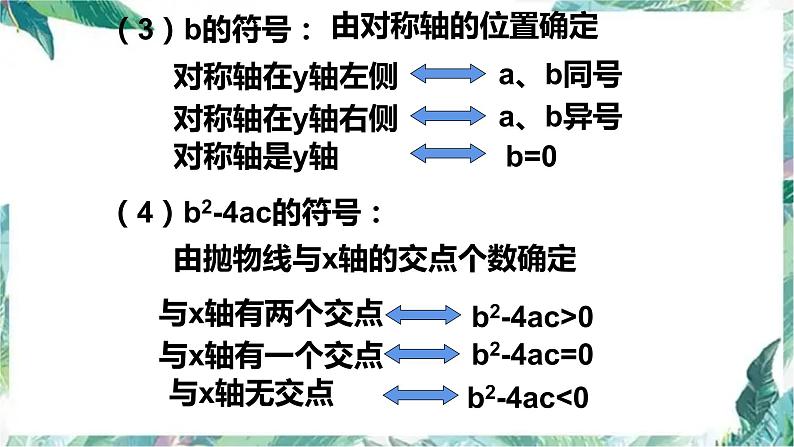
如何根据图像判别a、b、c、b2-4ac，2a+b，a+b+c的符号
由抛物线的开口方向确定
由抛物线与y轴的交点位置确定.
（4）b2-4ac的符号：
由抛物线与x轴的交点个数确定
二次函数y=ax2 与y=a（x-h)2+k的关系
可以看作互相平移得到的.
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
简记为：上下平移，括号外上加下减；左右平移，括号内左加右减.二次项系数a不变.
注意：当二次函数为y= ax2+bx+c，需先将二次函数化为顶点式再按平移的规律进行平移。
与x轴两交点横坐标及另一点坐标
知识点五：求抛物线解析式常用的三种方法
一般式 y=ax2+bx+c
顶点式 y=a(x-h)2+k
交点式 y=a(x-x1)(x-x2)
x1 =x2＝－b/2a
x ≠ x1的一切实数
知识点六：二次函数与一元二次方程，一元二次不等式的关系
y= ax2+bx+c
利用二次函数解决实际问题
利用图形的面积公式建立相应的函数关系式
根据相关线段的长度大于0确定自变量的取值范围
配方变形，或利用公式在自变量的取值范围内求它的最大值或最小值
建立函数关系式：总利润=单件利润×销售量或总利润=总售价-总成本.
涨价：要保证销售量≥0；降价：要保证单件利润≥0.
在自变量的取值范围内确定最大利润
能够将实际距离准确的转化为点的坐标；
②选择运算简便的方法.
2、在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为（ ）
1、函数 是二次函数，则a=_______
3、抛物线 向右平移1个单位，再向下平移2个单位，得到抛物线 ，则a+b+c=_____
4、 已知函数的图象如图所示，求函数解析式。
解： 设函数的解析式为：y=a(x-x1)(x-x2), 则x1=-1, x2=3, 于是 y=a(x+1)(x-3).∵抛物线过y 轴上的点（0，3），∴把这点坐标代入上面式子，得 3=-3a∴ a=-1.∴ 所求函数解析式为： y=-1(x+1)(x-3). 即 y= - x2+2x+3 .
5、二次函数 y=ax2+bx+c 的图象如图所示，试用 “ >、< 、=” 填空：（1）a 0,b 0, c 0;（2）a+b+c 0;（3）a-b+c 0;（4） △ 0；（5） 0.