

安徽省滁州市定远县九梓学校2021-2022学年八年级下学期期末考试数学试题(word版含答案)
展开九梓学校2021-2022学年度下学期八年级期末考试卷
数学试题
一、选择题(本大题共10小题,每小题4分,满分40分)
1.要使有意义,x的取值范围是( )
A.x≥101 B.x≤101 C.x>101 D.x<101
2.用配方法解方程时,原方程应变形为( )
A. B. C. D.
3.电影《我和我的祖国》一上映就受到观众热烈追捧,第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达10亿元.若设增长率为x,则根据题意可列方程为( )
A. B.
C. D.
4.如图,在的正方形网格中,若小正方形的边长是1,则任意两个格点间的距离不可能是( )
A. B. C.3 D.
5.在ABC中,三边长分别为a,b,c,且,,则ABC是( )
A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形
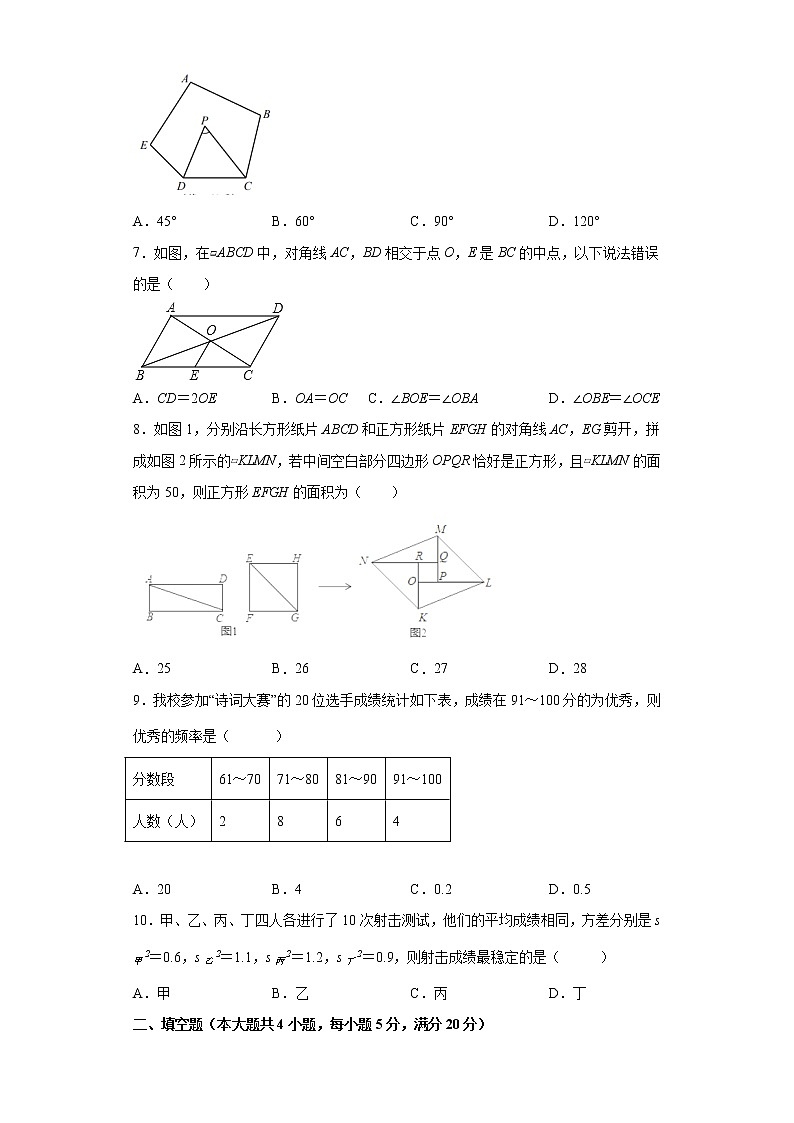
6.五边形中,,如图,、分别平分、,则( )
A.45° B.60° C.90° D.120°
7.如图,在▱ABCD中,对角线AC,BD相交于点O,E是BC的中点,以下说法错误的是( )
A.CD=2OE B.OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE
8.如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱KLMN,若中间空白部分四边形OPQR恰好是正方形,且▱KLMN的面积为50,则正方形EFGH的面积为( )
A.25 B.26 C.27 D.28
9.我校参加“诗词大赛”的20位选手成绩统计如下表,成绩在91~100分的为优秀,则优秀的频率是( )
分数段 | 61~70 | 71~80 | 81~90 | 91~100 |
人数(人) | 2 | 8 | 6 | 4 |
A.20 B.4 C.0.2 D.0.5
10.甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是s甲2=0.6,s乙2=1.1,s丙2=1.2,s丁2=0.9,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(本大题共4小题,每小题5分,满分20分)
11.函数中,自变量x的取值范围是________.
12.如图,某生物兴趣小组要在长40米、宽30米的矩形园地种植蔬菜,为便于管理,要在中间开辟一横两纵共三条等宽小路,若蔬菜种植面积为1008平方米,则小路的宽为_____米.
13.如图,正方形ABCD的边长是5,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是_____.
14.已知一组数据a、b、c、d、e的方差为,则新的数据2a﹣1、2b﹣1、2c﹣1、2d﹣1、2e﹣1的方差是 ______.
三、解答题(本大题共9题,满分90分)
15.(满分8分)观察下列等式,解答下面的问题:
①=2;
②=3
③=4
……
(1)请直接写出第⑤个等式是: (不用化简);
(2)根据上述规律猜想:若n为正整数,请用含n的式子表示第n个等式,并给予证明;
(3)利用(2)的结论计算.
16.(满分8分)已知关于x的方程.
(1)若方程总有两个不相等的实数根,求m的取值范围;
(2)若两实数根,满足,求m的值.
17.(满分8分)在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点.
(1)在图1中,以格点为顶点画,使三边长分别为、、;
(2)如图2,各顶点均在格点上,求的面积和点到的距离;
(3)在图3中,以格点为顶点画直角边长为无理数的等腰直角三角形,并说明理由.
18.(满分10分)在学习了算术平方根和二次根式等内容后,我们知道以下的结论:
结论①:若实数时,;结论②:对于任意实数,.
请根据上面的结论,对下列问题进行探索:
(1)若,化简:.
(2)若,,且,求的值.
(3)若有意义,化简.
19.(满分10分)如图,在中,,于点,,分别交,于点、,连接.
(1)判断的形状,并说明理由;
(2)若,求证:.
20.(满分10分)一款服装每件进价为80元,销售价为120元时,每天可售出20件,为了扩大销售量,增加利润,经市场调查发现,如果每件服装降价1元,那么平均每天可多售出2件.
(1)每件服装降价多少元时,能让利于顾客并且商家平均每天能赢利1200元.
(2)商家能达到平均每天赢利1800元吗?请说明你的理由.
21.(满分10分)为了了解某小区居民用水情况,从该小区的A、B两幢楼中各随机抽取25户的五月份用水量,并将所得用水量数据分成五组,如下表所示:
组别 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
用水量/立方米 |
将收集的数据进行整理、分析后,得到如下信息:
①A楼25户居民用水量的频数分布直方图如下图.
②A楼第三组数据(单位:立方米)是:10,10,10.1,10.9,11.4,11.5,11.6,10.8
③已知A、B两幢楼的样本数据的平均数和中位数如下表.
| 平均数 | 中位数 |
A楼 | 10.8 | n |
B楼 | 11 | 11.5 |
根据以上信息,解答下列问题:
(1)表格中的______;
(2)若A楼的样本数据中高于其平均数的有a个,B楼的样本数据中高于其平均数的有b个,请比较a、b的大小;并说明理由;
(3)若A楼共有180户居民、若B楼共有120户居民,则这两幢楼平均每户的用水量约是多少立方米?
22.(满分12分)如图,已知AD,BE,CF是△ABC的中线,且交于点O(O是△ABC的重心),G为BO的中点,H为OC的中点.
(1)求证:四边形EFGH为平行四边形;
(2)若OA=5,OB=3,OC=4,求△ABC的面积;
(3)若四边形EFGH为菱形,求证:AB2+AC2=5BC2.
23.(满分14分)如图正方形,点、、分别在、、上,与相交于点.
(1)如图1,当,
①求证:;
②平移图1中线段,使点与重合,点在延长线上,连接,取中点,连接,如图2,求证:;
(2)如图3,当,边长,,则的长为_________(直接写出结果).
参考答案
1.A
2.B
3.D
4.A
5.A
6.B
7.D
8.A
9.C
10.A
11.且
12.2
13.
14.
15.(1)解:第⑤个等式:;
故答案为;
(2)解:第个等式为:为正整数);
证明:左边,
为正整数
左边右边,
猜想成立;
(3)解:原式
.
16.(1)m>0
(2)
(1)解: ,
∵方程总有两个不相等的实数根,
∴8m>0,
∴m>0.
(2)解:由,
∵,,
∴原式,
整理得,
解得或,
∵m>0,
故m的值为.
17.(1)解:如图所示.
、、;
(2)解:作,垂足为.
根据题意得:,,
∵,
∴.
(3)解:如图所示,
如图1所示:
∵,,
,,
∴,
∴为直角边长为无理数的等腰直角三角形.
如图2所示:
∵,,
,,∴,
∴为直角边长为无理数的等腰直角三角形.
18.(1)5-2m (2)±12 (3)2m-3
(1)解:∵m<2,
∴m-2<0,m-3<0,
∴
=|m-2|+|m-3|
=2-m+3-m
=5-2m;
(2)解:∵,
∴|a|=4,
∴a=±4,
∵|b|=8,
∴b=±8,
∵,
∴a=4,b=8或a=-4,b=-8,
当a=4,b=8时,则a+b=4+8=12,
当a=-4,b=-8时,则a+b=-4-8=-12,
∴a+b=±12;
(3)解:∵有意义
∴m-2≥0,
∴m≥2,
∴1-m<0,
∴A=m-2+m-1
=2m-3.
19.(1)解:为等腰直角三角形.理由如下:
∵,,,
∴,
∴垂直平分,
∴,
∴,
∴,
∴为等腰直角三角形.
(2)证明:如图,在上取点,使,连接,
∵,,
∴,
∴,
∴,
又∵,
在和中,
,
∴,
∴,,
∴,
∴,
由(1)知:,,
∴,
∴在中,,
∴.
20. (1)解:设每件服装降价元,则销售量为件,
根据题意可得:,
化简得:,
解得:,,
又因为需要让利于顾客,所以,
答:每件服装降价20元时,能让利于顾客并且商家平均每天能赢利1200元.
(2)解:设每件服装降价元,
根据题意可得:,
化简得:,
∵,
∴此方程无解.
因此不可能每天盈利1800元.
21.(1)解:A楼25户居民用水量从小到大排列,排在第13位的数是10.1立方米,故中位数n=10.1,
故答案为:10.1;
(2)
解:A楼的样本数据中高于其平均数的有11户,故a=11;因为B楼的平均数为11,中位数为11.5,所以B楼的样本数据中高于其平均数不少于13户,即b≥13,
故a<b;
(3)解:=10.88(立方米),
答:这两幢楼平均每户的用水量约是10.88立方米.
22.(1)证明:∵BE、CF为中线,
∴AF=BF,AE=CE,
∴EF∥BC,EF=BC,
∵G,H分别是OB,OC的中点,
∵OG=BG,OH=CH,
∴GH∥BC,GH=BC,
∴FE∥GH,EF=GH,
∴四边形EFGH为平行四边形;
(2)解:∵E为AC的中点,H为OC的中点,
∴EH=OA=,
∵四边形EFGH为平行四边形,
∴OE=OG=OB=,OF=OH,
∵OC=4,
∴OH=OC=2,
∵OE2+OH2=() 2+22=,EH2=,
∴OE2+OH2=EH2,
∴∠EOH=90°,
∴S△EOC=OE•OC=××4=3,
∵AE=CE,
∴S△AOC=2S△EOC=6,
∴S△BOC=OB•OC=×3×4=6,
∵OF=OH,OH=OC,
∴OC=2OF,
∴S△BOF=3,
∴S△AOB=6,
∴S△ABC=S△AOC+S△AOB+S△BCO=6+6+6=18;
(3)证明:∵四边形EFGH为菱形,
∴EG⊥FH,
∴∠EOC=∠BOF=∠BOC=90°,
∴OE2+OC2=CE2=(AC) 2=AC2,OF2+OB2=BF2=AB2,OB2+OC2=BC2,
∴OE2+OC2+OB2+OF2= (AC2+AB2),
即BC2+BF2= (AC2+AB2),
∴BC2+(BC) 2= (AC2+AB2),
∴AB2+AC2=5BC2.
23.解:(1)①过点D作DM//GH交BC的延长线于点M,如图1,
∵四边形ABCD是正方形,
∴AD∥BC,∠ADC=90°,
又∵DM∥GH,
∴四边形DGHM是平行四边形,
∴GH=DM,GD=MH,
∴∠GOD=∠MDE=90°,
∴∠MDC+∠EDC=90°,
∵∠ADE+∠EDC=90°,
∴∠MDC=∠ADE,
在△ADE和△CDM中,
∴△ADE≌△CDM(AAS),
∴DE=DM,
∴DE=GH;
②在BC上截取BN=BE,如图2,
则△BEN是等腰直角三角形,EN=BE,
由(1)知,△ADE≌△CDH,
∴AE=CH,
∵BA=BC,BE=BN,
∴CN=AE=CH,
∵PH=PE,
∴PC=EN,
∴PC=BE,
∴BE=PC;
(2)如图3,过点D作DN//GH交BC于点N,则四边形GHND是平行四边形,
∴DN=HG,GD=HN,
∵∠C=90°,CD=AB=3,HG=DN=,
∴,
∴BN=BC-CN=3-1=2,
作∠ADM=∠CDN,DM交BA延长线于M,
在△ADM和△CDN中,
∴△ADM≌△CDN(AAS),
∴AM=NC,∠ADM=∠CDN,DM=DN,
∵∠GOD=45°,
∴∠EDN=45°,
∴∠ADE+∠CDN=45°,
∴∠ADE+∠ADM=45°=∠MDE,
在△MDE和△NDE中,
∴EM=EN,
即AE+CN=EN,
设AE=x,则BE=3-x,
在Rt△BEN中,22+(3-x)2=(x+1)2,
解得:x=,
∴
2023年安徽省滁州市定远县九梓学校中考一模数学试题(含答案): 这是一份2023年安徽省滁州市定远县九梓学校中考一模数学试题(含答案),共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023年安徽省滁州市定远县九梓学校中考一模数学试题(含答案): 这是一份2023年安徽省滁州市定远县九梓学校中考一模数学试题(含答案),共20页。试卷主要包含了05等内容,欢迎下载使用。
安徽省滁州市定远县九梓学校2021-2022学年八年级下学期期末数学试卷(word版含答案): 这是一份安徽省滁州市定远县九梓学校2021-2022学年八年级下学期期末数学试卷(word版含答案),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












