
数学七年级上册2.1 有理数的加法教学设计
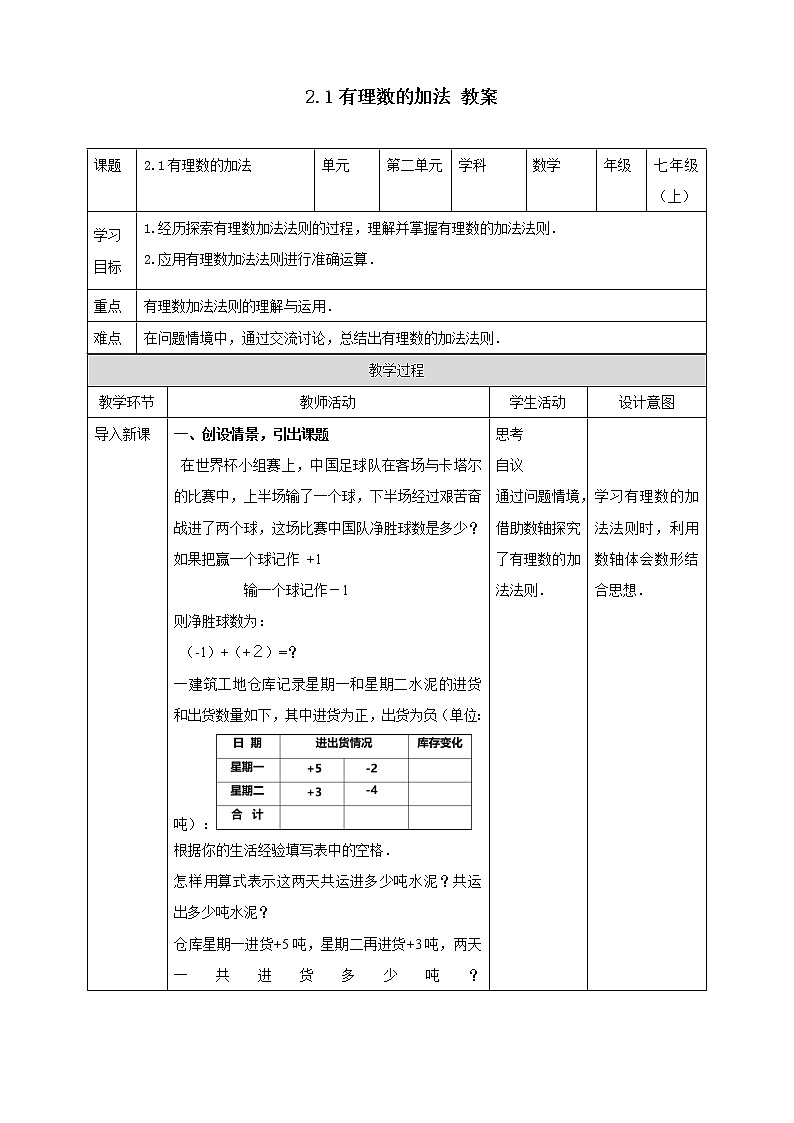
展开2.1有理数的加法 教案
课题 | 2.1有理数的加法 | 单元 | 第二单元 | 学科 | 数学 | 年级 | 七年级(上) |
学习 目标 | 1.经历探索有理数加法法则的过程,理解并掌握有理数的加法法则. 2.应用有理数加法法则进行准确运算. | ||||||
重点 | 有理数加法法则的理解与运用. | ||||||
难点 | 在问题情境中,通过交流讨论,总结出有理数的加法法则. | ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 | ||||||||
导入新课 | 一、创设情景,引出课题 在世界杯小组赛上,中国足球队在客场与卡塔尔的比赛中,上半场输了一个球,下半场经过艰苦奋战进了两个球,这场比赛中国队净胜球数是多少? 如果把赢一个球记作 +1 输一个球记作-1 则净胜球数为: (-1)+(+2)=? 一建筑工地仓库记录星期一和星期二水泥的进货和出货数量如下,其中进货为正,出货为负(单位:吨): 根据你的生活经验填写表中的空格. 怎样用算式表示这两天共运进多少吨水泥?共运出多少吨水泥? 仓库星期一进货+5吨,星期二再进货+3吨,两天一共进货多少吨?
列式:(+5)+(+3)= +8 仓库星期一出货2吨,星期二再出货4吨,两天一共出货多少吨? 列式:(-2)+(-4)= -6 在数轴上表示以下同号两数相加,并写出结果. (1)(+2)+(+4)=_____________;+6 (2)(-3)+(-3)=_____________ .-6 从上面问题中,你能得出同号两数相加的方法吗? 同号两数相加,取与加数相同的符号,并把绝对值相加. 在数轴上表示以下异号两数相加,并写出结果. (1)(+6)+(-3)= __________ .+3 (2)(-5)+(+4)= ______ .-1 从上面问题中,你能得出异号两数相加的方法吗? 异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值. 有理数相加的其他法则: 互为相反数的两个数相加得零;一个数同零相加,仍得这个数. 举例:-6+6=0,-5+0=-5
| 思考 自议 通过问题情境,借助数轴探究了有理数的加法法则. |
学习有理数的加法法则时,利用数轴体会数形结合思想.
| ||||||||
讲授新课 | 二、提炼概念 有理数的加法法则 1. 同号两数相加,取相同的符号,并把绝对值相加。 2. 异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;互为相反数的两个数相加得零。 3. 一个数同零相加,仍得这个数。 三、典例精讲 例1 计算下列各式: (1)(-11)+(-9);(2)(-3.5)+(+7); (3)(-1.08)+0; (4) .
归纳:两个有理数相加,在判断加数类型的基础上,先确定和的符号,再确定和的绝对值. 例2 某市今天的最高气温为7℃,最低气温为0℃.据天气预报,两天后有一股强冷空气将影响该市,届时将降温5℃.问两天后该市的最高气温、最低气温约为多少摄氏度? 解:气温下降5℃,记为-5℃. 7+(-5)=2(℃);0+(-5)=-5(℃). 答:两天后该市的最高气温约为2℃, 最低气温约为-5℃.
|
掌握有理数加法的一般步骤,同时关注分类讨论、数形结合等研究问题的方法.
|
通过设置问题情境,借助数轴,感受分类讨论、数形结合思想,同时引导学生自主探索、合作交流,着力培养学生的观察、比较、探究、归纳能力.
| ||||||||
课堂检测 | 四、巩固训练 1. 下列结论正确的有 ( ) ①两个有理数相加,和一定大于每一个加数; ②一个正数与一个负数相加得正数; ③两个负数和的绝对值一定等于它们的绝对值的和;④两个正数相加,和为正数; ⑤正数加负数,其和一定等于0. A.0个 B.1个 C.2个 D.3个 答案:C 2.已知a,b,c在数轴上对应的点的位置如图所示. 比较大小(填“>”或“<”): a+b____0,a+c____0,<,< b+c____0,b+(-a)____0,<,> b+(-c)____0,(-b)+c____0,<,> (-b)+(-c)____0,(-a)+(-c)____0. >,> 3.计算:(1)(-3)+(-12); (2)(-1.25)+1.75; (3)(-)+;(4)(-3)+(+2). 解:(1)(-3)+(-12)=-15; (2)(-1.25)+1.75=0.5; (3)(-)+=-+=-;(4)(-3)+(+2)=-+=-+=-. 4. 下表列出了国外几个城市与北京的时差(带正号的数表示同一时刻比北京时间早的时数)
(1)如果北京时间14:00,那么三个地区的时间分别是多少? (2)如果小明想给远在纽约旅游的爸爸打电话,他在北京时间下午2:00打电话,你认为合适吗?说明理由. 解:(1)14+(-13)=14-13=1,纽约的时间为凌晨1点; 14+(-7)=14-7=7,巴黎的时间为早上7点; 14+(+1)=14+1=15,东京为下午三点. (2)由(1)知,此时纽约的时间为凌晨1点,故不合适.
|
|
| ||||||||
课堂小结 |
|
|
|
初中浙教版2.1 有理数的加法教案及反思: 这是一份初中浙教版2.1 有理数的加法教案及反思,共3页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。
初中数学浙教版七年级上册2.1 有理数的加法教案: 这是一份初中数学浙教版七年级上册2.1 有理数的加法教案,共5页。教案主要包含了创设情景,引出课题,典例精讲,巩固训练等内容,欢迎下载使用。
数学七年级上册2.1 有理数的加法教案: 这是一份数学七年级上册2.1 有理数的加法教案,共6页。教案主要包含了创设情景,引出课题,典例精讲,巩固训练等内容,欢迎下载使用。













