初中数学2 矩形的性质与判定完美版ppt课件

这是一份初中数学2 矩形的性质与判定完美版ppt课件，文件包含121《矩形的性质》课件PPTpptx、121《矩形的性质》教案docx等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

观察下面图形,长方形在生活中无处不在.
你还能举出其他的例子吗？
长方形跟我们前面学习的平行四边形有什么关系？
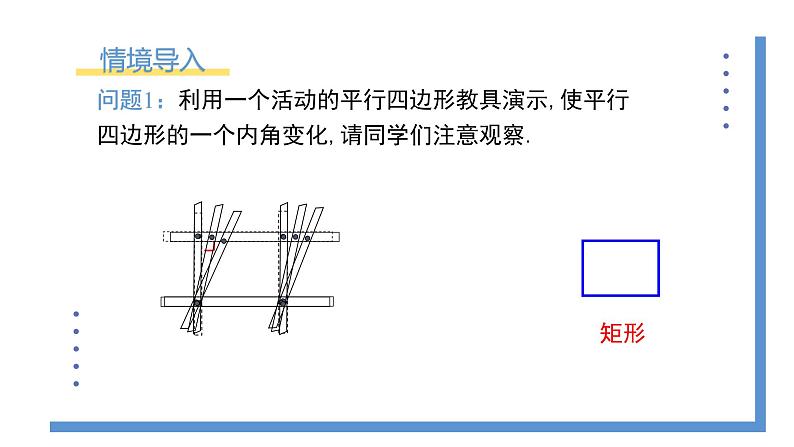
问题1：利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.
定义：有一个角是直角的平行四边形叫做矩形.
平行四边形不一定是矩形.
矩形是特殊的平行四边形,它具有平行四边形的所有性质,但平行四边形不一定是矩形.
矩形是特殊的平行四边形，它具有一般平行四边形的所有性质。
可以从边，角，对角线等方面来考虑.
准备素材：直尺、量角器、橡皮擦、课本、铅笔盒等.（1）请同学们以小组为单位,测量身边的矩形（如书本,课桌,铅笔盒等）的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.
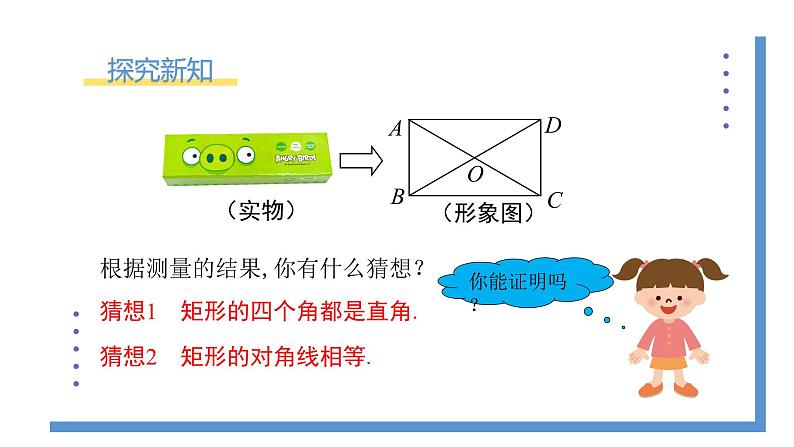
根据测量的结果,你有什么猜想？
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
已知：如图，四边形ABCD是矩形，∠ABC＝90°，对角线AC 与DB 相交于点O. 求证：（1）∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°； （2） AC=DB. 证明：∵四边形ABCD是矩形， ∴∠ABC＝∠CDA，∠BCD＝∠DAB(矩形的 对角相等)，AB∥DC(矩形的对边平行)． ∴∠ABC＋∠BCD＝180°. 又∵∠ABC＝90°，∴∠BCD＝90°. ∴∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°.
已知：如图，四边形ABCD是矩形，∠ABC＝90°，对角线AC 与DB 相交于点O. 求证：（1）∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°； （2） AC=DB. （2）∵四边形ABCD是矩形， ∴AB=CD（矩形的对边相等）. 在△ABC和△DCB中， ∵AB=DC，∠ABC=∠DCB，BC=CB， ∴△ABC≌△DCB， ∴AC=DB.
矩形除了具有平行四边形所有性质，还具有的性质有：矩形的四个角都是直角. 矩形的对角线相等.
数学语言：在矩形ABCD中，对角线AC与DB相交于点O.∠ABC=∠BCD=∠CDA=∠DAB =90°，AC=DB.
动手操作：准备一张长方形纸片，通过折叠纸片你能发现什么？
矩形是_____________；矩形有____条对称轴。
1.矩形具有而平行四边形不一定具有的性质是（   ）A．内角和是360度                B．对角相等C．对边平行且相等                D．对角线相等
如图，一张矩形纸片，画出两条对角线，沿着对角线AC剪去一半.
问题 ： Rt△ABC中，BO是一条怎样的线段？它的长度与斜边AC有什么关系？
猜想：直角三角形斜边上的中线等于斜边的一半.
证明:延长BO至D, 使OD=BO, 连接AD、DC.
∵AO=OC,BO =OD，∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∴平行四边形ABCD是矩形，
定理：直角三角形斜边上的中线等于斜边的一半.
直角三角形斜边上的中线等于斜边的一半.
数学语言：在△ABC中，∵∠ABC=90°，AO=CO，
例1.如图，在矩形ABCD中，两条对角线相交于点O，∠AOD=120°，AB=2.5，求这个矩形的对角线的长.
∴OA=OD. ∵∠AOD=120°，
∴BD=2AB=2×2.5=5.
（1）直角三角形的两个锐角互余.（2）勾股定理：直角三角形的两条直角边的平方和等于斜边的平方.（3）直角三角形中，30°角所对的直角边等于斜边的一半.（4）直角三角形斜边中线等于斜边的一半.
直角三角形的性质小结：
2．（2022安徽中考）两个矩形的位置如图所示，若∠1＝α，则∠2＝（　　）
A．α﹣90°B．α﹣45°C．180°﹣αD．270°﹣α
3．（2022青海中考）如图，矩形ABCD的对角线相交于点O，过点O的直线交AD，BC于点E，F，若AB＝3，BC＝4，则图中阴影部分的面积为 　　．
4．（2022十堰中考）“美丽乡村”建设使我市农村住宅旧貌变新颜，如图所示为一农村民居侧面截图，屋坡AF，AG分别架在墙体的点B，C处，且AB＝AC，侧面四边形BDEC为矩形．若测得∠FBD＝55°，则∠A＝　 　°．
5．（2022鄂州中考）如图，在矩形ABCD中，对角线AC、BD相交于点O，且∠CDF＝∠BDC、∠DCF＝∠ACD．（1）求证：DF＝CF；（2）若∠CDF＝60°，DF＝6，求矩形ABCD的面积．
解：（1）证明：∵四边形ABCD是矩形，∴OC＝ AC，OD＝ BD，AC＝BD，
∴OC＝OD，∴∠ACD＝∠BDC，∵∠CDF＝∠BDC，∠DCF＝∠ACD，∴∠CDF＝∠DCF，∴DF＝CF；
（2）解：由（1）可知，DF＝CF，
∴△CDF是等边三角形，
∵∠CDF＝∠BDC＝60°，OC＝OD，
∴△OCD是等边三角形
∵四边形ABCD是矩形
∴BC＝ =6
∴S矩形ABCD＝BC•CD＝6 ×6＝36
具有平行四边行的一切性质
四个内角都是直角，两条对角线互相平分且相等
直角三角形斜边上的中线等于斜边的一半
有一个角是直角的平行四边形叫做矩形