2022年高中名校自主招生初升高衔接数学讲义9 几何不等式 含答案
展开第九讲 几何不等式
知识要点
在自招考试中,求几何最值的问题频频出现,比如求最短距离、求某个角度的取值范围、求面积的最大值等等.所有这些问题都可以归结为几何不等式
有关几何不等式的性质和定理如下:
1.三角形两边之和大干第三边,两边之差小于第三边.
2.三角形的外角大于任一不相邻的内角.
3.同一三角形中,大角对大边,大边对大角.
4.两点之间线段最短.
5.两边对应相等的三角形中,所夹的角越大,则它所对的边越大
6.两边对应相等的三角形中,第三边越大,则它所对的角越大
7.直角三角形的斜边大干任一直角边
可以看到,几何不等式的基础大多源于三角形,所以关于三角形的不等式是占绝大多数的,而很多包括四边形、圆的问题都可以化为三角形中的不等关系,因此三角形中的各种不等式是我们讨论的一个重点.
另外需要注意的是,很多几何不等式实际上是代数不等式,还有相当一部分几何不等武的证明过程用到了经典的代数不等式,其中最常用的就是均值不等式.
例题精讲
- 如图9-1,矩形中,,若在、上各取一点、,使的值最小,求这个最小值.
- 已知正三角形的边长为1,点、、分别在、、上,,求的最大面积.
- 在锐角的边、、上各有一动点、、,求证:的周长达到最小当且仅当、、为的三条高.
- 已知点是四边形的边的中点,且,证明:.
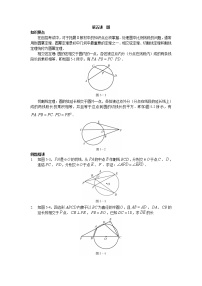
- 如图9-7,设的外心为.在其边和上分别取点和,使得.证明:的周长不小于边之长.
- 如图9-9,在的边上取一点,连结,过点作交于点,过点作交于点.求证:
- 如图9-10所示,在中,、、的对边分别为、、,如果,求证:.
- 求证:在凸四边形,有.
- 证明Ptolemy定理(托勒密定理):对于一般的四边形,有,当且仅当是圆内接四边形时等号成立.
习题巩固
- 如图所示,设,为上一点,,为上一点,,为上任意一点,是上任意一点,求折线的长度的最小值.
- 已知平面内的任意四点,其中任意三点不共线,试问:是否一定能从这样的四个点中选出三点构成一个三角形,使得这个三角形至少有一个内角不大于?试证明你的结论.
- 如图,点、、分别在、、上,若分别记、、为、、,证明:,当且仅当、、共点时等号成立.
- 如图,在的边上依次有点、,边上依次有点、
求证:.
- 如图,在中,、、的平分线分别交外接圆于点、、.
证明:.
- 设四边形四边依次为、、、,则其面积不大于
,
其中.取到最大值时,仅当四边形内接于圆.
- 设点为边长为1的正三角形内一点,则、、中至少有一条其长度不超过.
- 已知点是四边形的边的中点,且,证明:.
- 如图,已知中,,为内一点.求证:
.
- 如图所示,在四边形中,,,求证:
(1);
(2).
自招链接
- 已知为内一点,点至三边、、的距离分别为、、,求当取最小值时点的位置.
- 中,为三角形的重心,过的直线交边于点,交边于点.若的面积为1,求的面积的最大值与最小值.
参考答案
- 如图9-2,作点关于的对称点,连结,则点关于的对称点在上的点处.
此时
过点作于点,则,即的最小值为.
设和交于点,连结,则的面积等于
.
因为,则.
设,则,.
所以,解得.
所以,故的最小值是..
- 如图9-3,设,,,则,.
,于是问题变为求的最小值,展开后约去,即求的最大值.
由不等式知,当时,
,
此时的面积达到最大值.
- 如图9-4,设点关于、的对称点分别为点、,与交于点,与交于点,则
.
这里为的高,为的外接圆半径.
又由对称性,除了外,、也分别必须垂直于、时方能达到.
- 显然,要证题设的不等式,应当把、、三条线段首尾连结成一条折线,然后再与线段比较要实现这一构想,折线之首端应与点重合,尾端应与点重合,这可由轴对称来实现.
如图9-6,以为对称轴,作点关于的对称点,连接、,则,,即,由此.
再以为对称轴,作点关于的对称点,连结、,则,,即,由此.
而,所以
.
注意到
,
因此
,
而,所以是等边三角形,.
由于两点之间以直线段为最短,所以
,
即.
- 如图9-8,注意到,则在内部可取点和,使得,.
从而,,且
.
连结,则,故.
因此,
.
- 由知,且.
又由得,所以.
从而,即,所以
.
上式表明二次方程有实根,从而其判别式非负,即,故.
另解:对于,可以配方得
,
即得结论.
- 注意到,所以等价于.
如图9-11所示,延长至点,使,延长至点,使,则.
过点作的平行线,过点作的平行线,两线交于点,连结,则四边形为平行四边形.
则,.
因为,,,故,则,,即,.
从而,在中,.
而,故,即.
- 如图9-12,取的中点,的中点,连结、、,令,,,则由余弦定理得
,
,
而,,
所以.
同理可得
,
,
于是有
.
因为,所以
.
说明:(1)当时,,且有四边形为平行四边形.因此我们有结论:
平行四边形的四边长平方和等于对角线长的平方和.
反过来,若四边形的四边长平方和等于对角线长的平方和,则此四边形为平行四边形
(2)运用余弦(或正弦)定理得到几何线段的不等式,是其思路之一.
- 如图9-13,作线段,且.
则有,可得,所以,所以
.①
又因为
.
所以,所以.即
.
得到
.
当且仅当在上时
,
此时,即、、、四点共圆.
习题巩固
- 构造点关于的对称点,点关于的对称点,则
.
在中,,,,解得,即折线的长度的最小值为12.
- 一定可以从中选出三点符合题意.根据内角的大小,分凸四边形或凹四边形分类讨论即可.
- 设,,,则
,,,
所以
.
又有,
故,
于是命题得证.当且仅当时取等号,由塞瓦逆定理知,此时必有、、共点.
- 设.而
,
即,
所以.
- 如图,连结、、、、、.
因为,,,所以、、相交于一点,即为的内心,则,,.
在中,因为,所以.
同理可证,.
将这三个式子相加并整理,得
.①
因为,,,所以
.②
式得.
- 如图,连结、,交于点,设,则由四边形的余弦定理,得.
又,两式平方后相加,得
,
即
.
由托勒密不等式,有,故
.
由托勒密定理知,仅当内接于圆时,面积取最大值.
- 设为的重心,则.
分别以、、为圆心,经过点作圆,将分为如图所示的6个区域.
当点在区域Ⅰ时,显然有.
同样地,在区域Ⅱ、Ⅲ时,分别有,.
当点在区域Ⅳ时,,至少有一个成立.同样地,在区域Ⅴ时,,至少有一个成立,在区域Ⅵ时,,至少有一个成立.
综上所述,、、中至少有一条不超过.
- 同例4.
- 将三角形逆时针旋转,通过两点之间线段最短得证.
- (1)以为对称轴将翻折到的位置,则由可知在上,且,.
将平移到的位置,则由可知在的延长线上,且,,因此是一个等腰梯形,所以,于是
.
(2)由(1)可得,即
,
而由及勾股定理可得,故.
自招链接
- 显然有,而由柯西不等式
.
即有.
上式右边即为最小值,等号当且仅当时取到,即点是的内心.
- 设,由为三角形重心可得.
.
因为,可得,.
则.
根据的取值范围,可得,所以最小值为,最大值为.
即的面积的最大值为,最小值为.
2022年高中名校自主招生初升高衔接数学讲义12 高斯函数 含答案: 这是一份2022年高中名校自主招生初升高衔接数学讲义12 高斯函数 含答案,共8页。
2022年高中名校自主招生初升高衔接数学讲义10 数论 含答案: 这是一份2022年高中名校自主招生初升高衔接数学讲义10 数论 含答案,共8页。
2022年高中名校自主招生初升高衔接数学讲义8 几何计算 含答案: 这是一份2022年高中名校自主招生初升高衔接数学讲义8 几何计算 含答案,共20页。