2022年高中名校自主招生初升高衔接数学讲义3 函数 含答案

第三讲  函数

知识要点

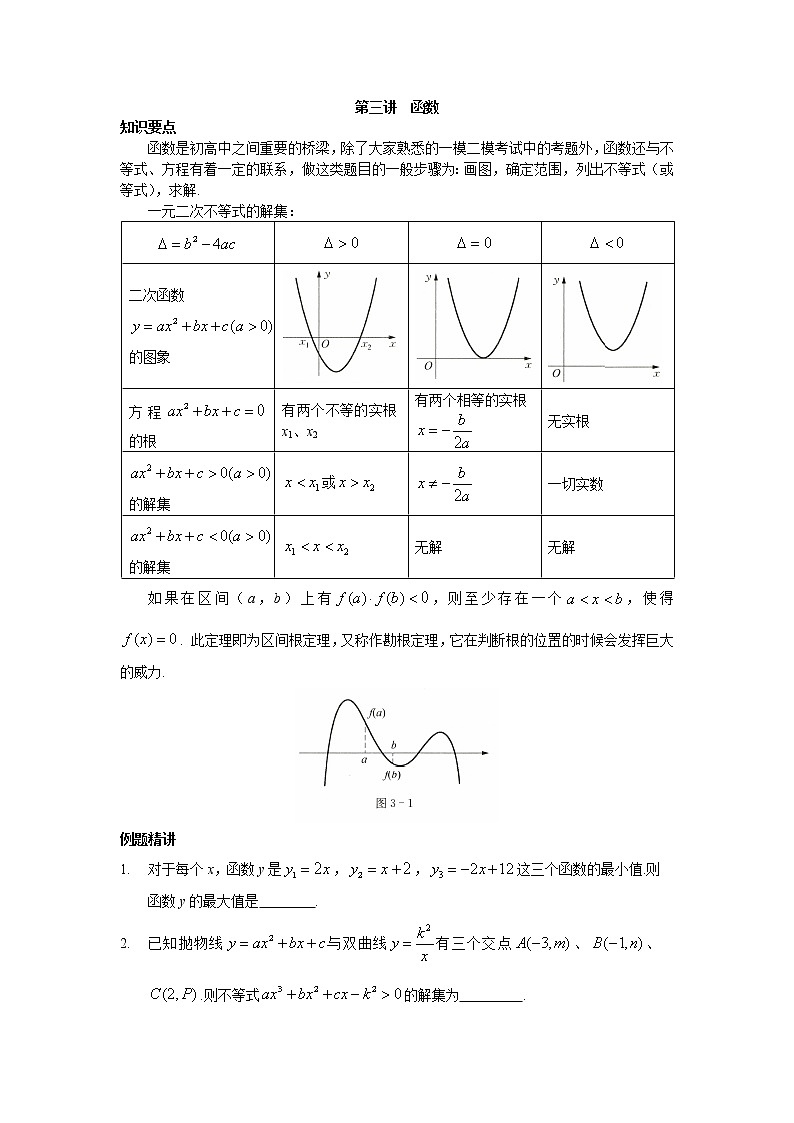
函数是初高中之间重要的桥梁，除了大家熟悉的一模二模考试中的考题外，函数还与不等式、方程有着一定的联系，做这类题目的一般步骤为：画图，确定范围，列出不等式（或等式），求解.

一元二次不等式的解集：

如果在区间（a，b）上有，则至少存在一个，使得. 此定理即为区间根定理，又称作勘根定理，它在判断根的位置的时候会发挥巨大的威力.

例题精讲

1. 对于每个x，函数y是，，这三个函数的最小值.则函数y的最大值是        .
2. 已知抛物线与双曲线有三个交点、、.则不等式的解集为         .
3. 已知函数且使成立的x的值恰好有三个，则k的值为       .
4. 求的最小值.
5. 若二次函数的图象的顶点在第一象限，且过点（0，1）和（－1，0），则的值的变化范围是（    ）.

（A）     （B）

（C）     （D）

6. （1）画出的函数图象；

（2）根据图象求出方程

的解.

7. 已知二次函数（其中a、b、c为整数且a≠0），对一切实数x恒有，求此二次函数的解析式.
8. 若抛物线与连结两点M（0，1）、N（2，3）的线段MN（包括M、N两点）有两个不同的交点，求m的取值范围.
9. 已知a、b、c为正整数，且抛物线与x轴有两个不同的交点A、B. 若A、B到原点的距离都小于1，求的最小值.
10. 二次函数，，，求M的最小值.
11. 二次函数满足：（1）；（2）对任意实数x有成立，求.
12. 问同时满足条件：（1）当时，；（2）的二次函数是否存在？证明你的结论.
13. 已知，求证：

    .

14. 已知.

（1）若有实根，求证：也有实数根；

（2）若无实数根，求证：也无实数根.

习题巩固

15. 求函数的最大值.
16. 若对任意实数x，不等式恒成立，求实数a的取值范围.
17. 求函数（2016层绝对值符号）与x轴围成的闭合图形的面积.
18. 已知实数a、b、c满足，，，求的取值范围.
19. 求证：对一切实数a，方程至少有一个实根.
20. 设a、b是实数，二次函数满足，. 求的取值范围.
21. 若方程有一根小于，其余三根都大于，求m的取值范围.
22. 二次函数，若时，，求m、n、k应满足的条件.
23. 设函数，当时，，求a、b.
24. 已知，且，. 求证：有一根x0，满足.
25. 已知满足6a、2b、、d均为整数，求证：对任意的整数x，均取整数值.
26. 二次函数满足时，求的解析式.
27. 二次函数满足，，求的最小值.
28. 求所有的二次函数，a、b为实数，且存在三个取自1，2，3，…，9的不同整数m、n、p，使得.
29. 试求实数a、b使得抛物线、与x轴有4个交点，且相邻两点之间的距离相等.

自招链接

30. 德国著名数学家狄利克雷在数学领域成就显著，以其命名的函数

该函数被称为狄利克雷函数，则关于狄利克雷函数有如下四个命题：

①；

②对任意恒有成立；

③任取一个不为零的有理数T，对任意的恒成立；

④存在三个点、、，使得△ABC为等边三角形.其中真命题的个数是（    ）.

A. 1   B. 2   C. 3   D. 4

31. 如图，该函数由分段的线性函数组合而成，由于形状像很多顶帽子，被称为“Euclid帽子函数”. 在数学、工程等领域的插值问题中有很高的应用价值.

（1）试写出其函数表达式；

（2）求二次函数与“Euclid帽子函数”的交点个数；

（3）试构造一个二次函数，使其与“Euclid帽子函数”有且只有两个交点，且两交点的横坐标都在和之间.

参考答案

1. 在同一坐标系内分别画出y1、y2、y3的图象，进而可得函数y的图象，易知，当时，y有最大值.
2. 两曲线的图象如图3-2，若，则，此时，.

若，则，此时，由图象知.

综上，不等式的解集为或.

3. 如图3-3，观察图象易知，直线y=3与函数图象恰有三个交点，即k=3时，使y=k成立的x的值恰好有三个交点.

4. .

几何意义：在平面直角坐标系中，点到点（0，1）与点（5，0）的距离之和.

原题即求：抛物线上的点P到与的距离之和最短是多少？易知.

5. 先来常规代数法.

将（0，1）和代入得：，，则化为.

顶点坐标在第一象限.

解不等式组：得，代入，得.

答案：D.

除了以上的做法，选择题我们还可以画图象（如图3-4）来解决.

点E在点D、F之间. 由对称轴的位置可知点D在点B的左边，那么E点位置也应在B点左侧；二次函数抛物线是曲线，从C点开始弯下去了，那么E点当然在F点下方，同学们可以画一画极端情况：相信你能发现0与2只能无限接近却无法达到.

6. 我们先来体会一下绝对值在函数图象中的表现.

如图3-5，比较一下与，图中虚线部分为，加了绝对值之后时的图象就变为实线部分，满足绝对值的意义，函数值为负的部分翻折上去变成正的了.

接着我们考虑：，这个大家都知道，是将向下平移3个单位，那么又会出现函数值为负的部分，所以得继续将负数部分翻折上去，如图3-6.

重复刚才的过程两次：将向下平移3个单位，再把负数部分翻折上去，得到；再向下平移3个单位，把负数部分翻折上去，得到，如图3-7.

（2）有了作图的经验，我们可以轻松画出

，

将两函数图象放一起，交点横坐标即为所求方程的解，我们还是来看图象（图3-8）：

两函数图象分别为实线和虚线，构成了很多等腰直角三角形，交点横坐标一目了然.

答案：.  

对一切实数x恒成立，由②得：.

令，则为开口向下且与x轴至多只有一个公共点的抛物线或为不在x轴上方的常值函数，又由①得，则或.

先讨论简单的：

当时，常值函数，则，.

由①得，即恒成立. 由，得，矛盾. 所以这种情况不存在.

当时，.

.

由①得，即恒成立. 则

.

结合③④，发现：，所以，即，得.

若，则c无整数解；若，则.

所以，，，，二次函数解析式为.

8. 线段MN的函数解析式为. 于是，原问题等价于方程在0—2之间有两个不同的实根. 整理，得.

令.

要使得在0—2之间内有两个不同实根，不仅要考虑端点，还要考虑判别式和对称轴，则有

解得.

9. 令，依题意，得：

由①得；由③得.

.

因为，则. 所以，.

从而，. 故.

因此，.

取，得，.

符合条件，因此，的最小值为11.

10. 由已知得：，，所以

所以.

又当时，，故M的最小值是.

11. 设.

由（1）知，所以.

由（2）知，所以，即，所以

.

从而  .

又因为，即

对任意x成立，故，从而，得，则

.

12. 假设存在满足条件的二次函数.

（1）当时，，则，，，则

矛盾.

所以不存在.

13. 若，不等式显然成立.

若，令

则  .

又二次项系数，所以抛物线与x轴有交点.

故，即

.

14. （1）若x0是的实数根，则，即是的实数根.

（2）若无实数根，当时，对于一切实数都成立，，所以无实数根. 同理当时，对于一切实数都成立，所以无实数根.

习题巩固

15. 注意到表示点到点、的距离之差的绝对值，则，于是，y最大值为，此时，.
16. 可分类讨论.

当时，，得，当时，，得a为任意实数；当时，. 由恒成立得.

另解：数形结合，只不过这次“形”用的是函数图象.

设，画出两个函数图象，满足恒成立，易见的斜率a的取值范围为.

17. 只有一层绝对值时，其面积为0，有两层绝对值时，其面积为1……有k层绝对值时，其面积为. 那么2016层绝对值，其面积为2015.
18. 由已知得则a、b是是方程的两根且.

所以

故. 又，则.

19. 设，则

，. 由至少有一个实根.

20. 由，

.

21. 令，则有两个正根. 一根小于1，另一根大于4.

.

又，所以且.

23. ，对称轴.

（1）当时，则.

（2）当时，则（舍去）.

（3）当时，则或（舍去）.

综上：或.

24. 设，由已知可得. 故

（1）若，则，即，.

（2）若，则. 若，则，.

若，则

，

.

综上，有一根x0满足.

25. .

因为6a、2b、、d均为整数，对任意的整数x，有、为整数，故对任意的整数x，均取整数值.

26. 由已知得，，则

，   ①

，   ②

   ③

由①+2②+③得，所以每个等号都成立，故.

27. 由已知，则

，

令，则.

当时等号成立，所以最小值为3.

28. 或或或
    .
29. 设与分别与x轴交于、；、，. 因为两抛物线有交点，所以由图象可知，即. 不妨设，故，. 可知两抛物线交点在第四象限，由图象可知：，则，且. 所以或（舍）.

综上，结合对称性得或.

自招链接

30. 这算考查函数思想的阅读理解题了吧，别怕，我们好歹学过一点函数知识，基本思想还是具备的，一个个来看.

命题①错：或0，为有理数，则，矛盾.

命题②对：当x为有理数时，也为有理数，；当x为无理数时，也为无理数，.

命题③对：当x为有理数时，也为有理数，；当x为无理数时，也为无理数，.

命题④对：由于、、只能取0或1，要构成三角形就不能同时取0，或同时取1，不妨设，则x1、x2为无理数，x3为有理数，作图看看能否构造；

x3随便取个有理数即可.

答案：C

31. （1）容易想到的就是写成分段函数：

（n为整数）.

也可以写成一个表达式，注意到图象中这段，恰好是

，

可以利用高斯函数达到目的：

，

其是[x]表示不大于x的最大整数.

或者根据前面例题总结的经验，写成这样的形式：

（偶数个绝对值）.

（2）求交点，先考虑图象法，图象法比较直观，但无法精确求值，如图：

由图象知：时，有2个交点，当时，有1个交点，当时没有交点.

注意：当a接近最高点的时候，需要验证一下这条直线（不含端点）和二次函数一定没有交点.

（3）.