

2022年广西桂林中考数学复习训练:第29讲 概率初步(含答案)
展开这是一份2022年广西桂林中考数学复习训练:第29讲 概率初步(含答案),共12页。试卷主要包含了下列事件中,属于不可能事件的是等内容,欢迎下载使用。
第二十九讲 概 率 初 步
1.(2021·湖州中考)下列事件中,属于不可能事件的是(D)
A.经过红绿灯路口,遇到绿灯
B.射击运动员射击一次,命中靶心
C.班里的两名同学,他们的生日是同一天
D.从一个只装有白球和红球的袋中摸球,摸出黄球
2.(2021·绍兴中考)在一个不透明的袋中装有6个只有颜色不同的球,其中3个红球、2个黄球和1个白球.从袋中任意摸出一个球,是白球的概率为(A)
A. B. C. D.
3.如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等.则小球从E出口落出的概率是(C)
A. B. C. D.
4.(2021·临沂中考)现有4盒同一品牌的牛奶,其中2盒已过期,随机抽取2盒,至少有一盒过期的概率是(D)
A. B. C. D.
5.不透明的袋子中装有红、蓝小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到相同颜色的小球的概率是____.
6.如表记录了某种幼树在一定条件下移植成活的情况:
移植总数n | 400 | 1 500 | 3 500 | 7 000 | 9 000 | 14 000 |
成活数m | 325 | 1 336 | 3 203 | 6 335 | 8 073 | 12 628 |
成活的频率 (精确到0.001) | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
由此估计这种幼树在此条件下移植成活的概率约__0.90__.(精确到0.01)
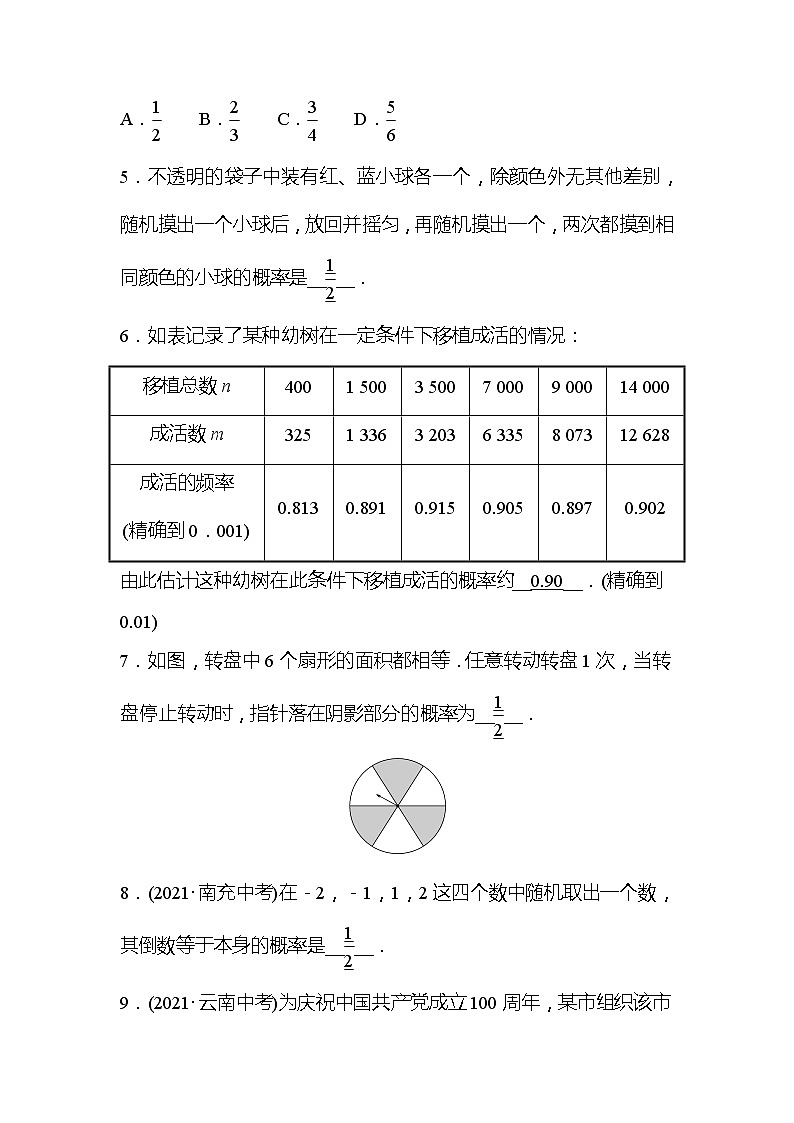
7.如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,指针落在阴影部分的概率为____.
8.(2021·南充中考)在-2,-1,1,2这四个数中随机取出一个数,其倒数等于本身的概率是____.
9.(2021·云南中考)为庆祝中国共产党成立100周年,某市组织该市七、八两个年级学生参加演讲比赛,演讲比赛的主题为“追忆百年历程,凝聚青春力量”.该市一中学经过初选,在七年级选出3名同学,其中2名女生,分别记为x1,x2,1名男生,记为y1;在八年级选出3名同学,其中1名女生,记为x3,2名男生,分别记为y2,y3.现分别从两个年级初选出的同学中,每个年级随机选出一名同学组成代表队参加比赛.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,求所有可能出现的代表队总数;
(2)求选出的代表队中的两名同学恰好是一名男生和一名女生的概率P.
【解析】(1)树状图如图所示:
由上可得,出现的代表队一共有9种可能性;
(2)由(1)可知,一共9种可能性,其中一男一女出现有5种,故选出的代表队中的两名同学恰好是一名男生和一名女生的概率P=.
10.小明和小刚一起做游戏,游戏规则如下:将分别标有数字1,2,3,4的4个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
【解析】这个游戏对双方不公平.
理由:列表如下:
| 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
所有等可能的情况有16种,其中两次数字差的绝对值小于2的情况有(1,1),(2,1),(1,2),(2,2),(3,2),(2,3),(3,3),(4,3),(3,4),(4,4)共10种,故小明获胜的概率为:=,小刚获胜的概率为:=,∵≠,∴这个游戏对两人不公平.
11.疫情期间,我市积极开展“停课不停学”线上教学活动,并通过电视、手机app等平台进行教学视频推送.某校随机抽取部分学生进行线上学习效果自我评价的调查(学习效果分为:A.效果很好;B.效果较好;C.效果一般; D.效果不理想),并根据调查结果绘制了如图两幅不完整的统计图:
(1)此次调查中,共抽查了________名学生;
(2)补全条形统计图,并求出扇形统计图中∠α的度数;
(3)某班4人学习小组,甲、乙2人认为效果很好,丙认为效果较好,丁认为效果一般.从学习小组中随机抽取2人,则“1人认为效果很好,1人认为效果较好”的概率是多少?(要求画树状图或列表求概率)
【解析】(1)80÷40%=200(名).
答案:200
(2)200-80-60-20=40(名),360°×=72°,补全条形统计图如图所示.
(3)用列表法表示所有可能出现的结果情况如下.
| 甲 | 乙 | 丙 | 丁 |
甲 | — | AA | BA | CA |
乙 | AA | — | BA | CA |
丙 | AB | AB | — | CB |
丁 | AC | AC | BC | — |
共有12种可能出现的结果,其中“1人认为效果很好,1人认为效果较好”即:1人为A,1人为B的有4种,∴P(1人认为效果很好,1人认为效果较好)==.
12.下列说法正确的是(B)
A.为了解人造卫星的设备零件的质量情况,选择抽样调查
B.方差是刻画数据波动程度的量
C.购买一张体育彩票中奖,是不可能事件
D.掷一枚质地均匀的硬币,正面朝上的概率为1
13.如图,电路图上有4个开关A,B,C,D和1个小灯泡,同时闭合开关A,B或同时闭合开关C,D都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是(B)
A.只闭合1个开关 B.只闭合2个开关
C.只闭合3个开关 D.闭合4个开关
14.(2021·安徽中考)如图在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是(D)
| ·A |
|
|
A. B. C. D.
15.(2021·重庆中考)在桌面上放有四张背面完全一样的卡片,卡片的正面分别标有数字-1,0,1,3.把四张卡片背面朝上,随机抽取一张,记下数字且放回洗匀,再从中随机抽取一张.则两次抽取卡片上的数字之积为负数的概率是____.
16.(2021·嘉兴中考)看了《田忌赛马》故事后,小杨用数学模型来分析:齐王与田忌的上、中、下三个等级的三匹马记分如表,每匹马只赛一场,两数相比,大数为胜,三场两胜则赢.已知齐王的三匹马出场顺序为10,8,6.若田忌的三匹马随机出场,则田忌能赢得比赛的概率为____.
马匹 | 下等马 | 中等马 | 上等马 |
齐王 | 6 | 8 | 10 |
田忌 | 5 | 7 | 9 |
17.(2021·成都中考)我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和.如图1,ar+cq+bp是该三角形的顺序旋转和,ap+bq+cr是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数z,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是____.
18.(2021·江西中考)为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从A,B,C,D四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字.
(1)“A志愿者被选中”是________事件(填“随机”或“不可能”或“必然”);
(2)请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A,B两名志愿者被选中的概率.
【解析】(1)“A志愿者被选中”是随机事件.
答案:随机
(2)列表如下:
| A | B | C | D |
A | — | (B,A) | (C,A) | (D,A) |
B | (A,B) | — | (C,B) | (D,B) |
C | (A,C) | (B,C) | — | (D,C) |
D | (A,D) | (B,D) | (C,D) | — |
由表可知,共有12种等可能结果,其中A,B两名志愿者被选中的有2种结果,
所以A,B两名志愿者被选中的概率为=.
19.(2021·泰安中考)为庆祝中国共产党成立100周年,落实教育部《关于在中小学组织开展“从小学党史,永远跟党走”主题教育活动的通知》要求,某学校举行党史知识竞赛,随机调查了部分学生的竞赛成绩,绘制成两幅不完整的统计图表.根据统计图表提供的信息,解答下列问题:
(1)本次共调查了________名学生;C组所在扇形的圆心角为________度;
(2)该校共有学生1 600人,若90分以上为优秀,估计该校优秀学生人数为多少?
(3)若E组14名学生中有4人满分,设这4名学生为E1,E2,E3,E4,从其中抽取2名学生代表学校参加上一级比赛,请用列表或画树状图的方法求恰好抽到E1,E2的概率.
竞赛成绩统计表(成绩满分100分)
组别 | 分数 | 人数 |
A组 | 75<x≤80 | 4 |
B组 | 80<x≤85 |
|
C组 | 85<x≤90 | 10 |
D组 | 90<x≤95 |
|
E组 | 95<x≤100 | 14 |
合计 |
|
|
【解析】(1)本次共调查的学生=14÷28%=50(人);
C组的圆心角为360°×=72°.
答案:50 72
(2)B组的人数为50×12%=6(人),
则D组的人数为50-4-6-10-14=16(人),
则优秀的人数为1 600×=960(人).
(3)画树状图为:
共有12种等可能的结果,其中恰好抽到E1,E2的结果数为2,
所以恰好抽到E1,E2的概率==.
【核心素养题】
下面是两个转盘,每个转盘分成几个相等的扇形,甲、乙两个人做游戏,游戏者同时转动两个转盘一次,如果转盘A转出了红色,转盘B转出了蓝色,则甲赢,否则乙赢.
(1)甲和乙获胜的概率分别是多少?
(2)这个游戏对双方公平吗?说说你的理由.
(3)如果你认为不公平,应怎样修改才能使游戏对双方公平?
【解析】(1)列表如下:
| 红 | 红 | 红 | 红 | 蓝 |
蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 蓝、蓝 |
蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 蓝、蓝 |
蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 蓝、蓝 |
蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 红、蓝 | 蓝、蓝 |
红 | 红、红 | 红、红 | 红、红 | 红、红 | 蓝、红 |
由表知,共有25种等可能结果,其中转盘A转出了红色,转盘B转出了蓝色有16种结果,
∴甲获胜的概率为,则乙获胜的概率为.
(2)不公平,因为≠,所以游戏不公平.
(3)两个转盘都转出蓝色,甲赢;两个转盘都转出红色,乙赢.
关闭Word文档返回原板块
相关试卷
这是一份2022年广西桂林中考数学复习训练:桂林五年真题 第1讲 实数(含答案),共3页。试卷主要包含了 eq \f 的倒数是,2 018的相反数是,2 017的绝对值是,9的平方根是,4的算术平方根是等内容,欢迎下载使用。
这是一份2022年广西桂林中考数学复习训练:第25讲 相似形(含答案),共9页。
这是一份2022年广西桂林中考数学复习训练:第3讲 分式(含答案),共6页。试卷主要包含了分式 eq \f 可变形为,定义一种新的运算,计算等内容,欢迎下载使用。








