数学选择性必修 第三册6.3 二项式定理课文课件ppt

这是一份数学选择性必修 第三册6.3 二项式定理课文课件ppt，共22页。PPT课件主要包含了二项式定理，二项展开式的通项，二项式的系数，二项式的系数的和，性质1对称性，a+bn，都等于2n－1，解得m＝6等内容，欢迎下载使用。

展开式中一共有n+1项．
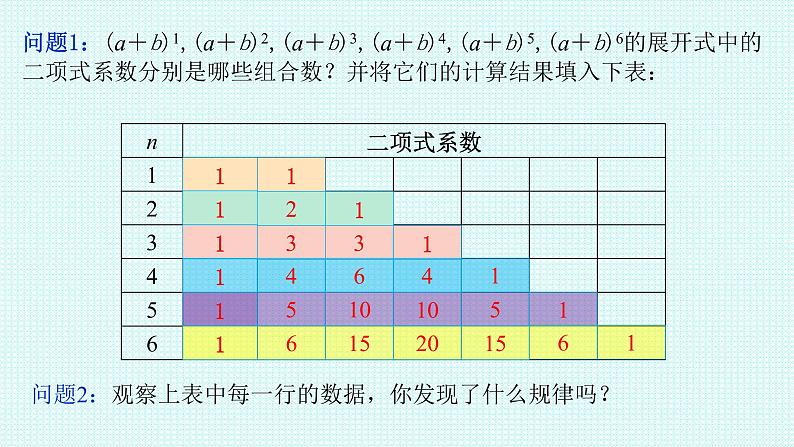
问题1：(a＋b)1,(a＋b)2,(a＋b)3,(a＋b)4,(a＋b)5,(a＋b)6的展开式中的二项式系数分别是哪些组合数？并将它们的计算结果填入下表：
问题2：观察上表中每一行的数据，你发现了什么规律吗？
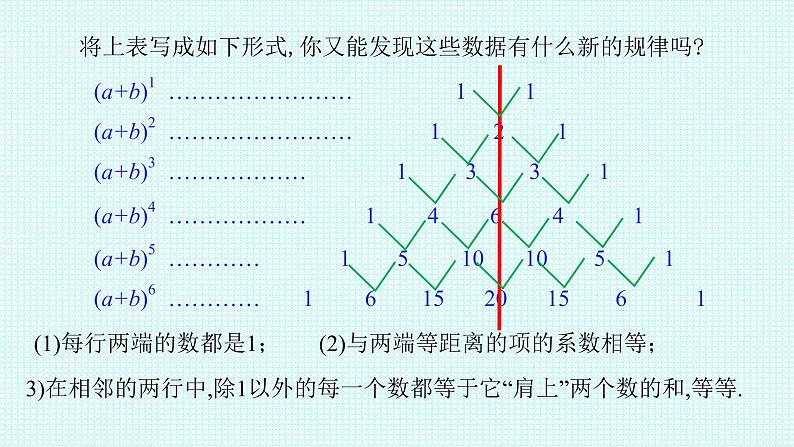
将上表写成如下形式,你又能发现这些数据有什么新的规律吗?
(1)每行两端的数都是1；
(2)与两端等距离的项的系数相等；
3)在相邻的两行中,除1以外的每一个数都等于它“肩上”两个数的和,等等.
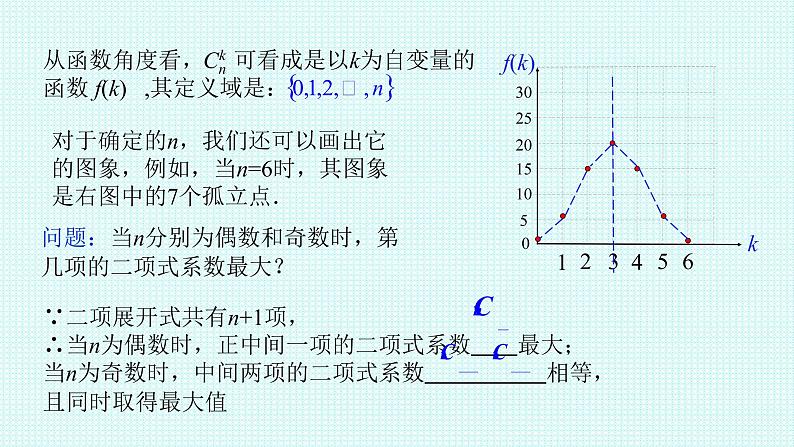
对于确定的n，我们还可以画出它的图象，例如，当n=6时，其图象是右图中的7个孤立点．
问题：当n分别为偶数和奇数时，第几项的二项式系数最大？
∵二项展开式共有n+1项，∴当n为偶数时，正中间一项的二项式系数 最大；当n为奇数时，中间两项的二项式系数 相等，且同时取得最大值
与首末两端“等距离”的两个二项式系数相等．
性质2：增减性与最大值
二项式系数是逐渐增大的，由对称性可知它的后半部分是逐渐减小的，即先增后减，所以在中间项取得最大值。
性质3：各二项式系数的和
（赋值法）令a=1，b=1，则
例1 求证：在(a+b)n的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和．
奇数项的二项式系数的和
偶数项的二项式系数的和
∴不妨令a=1，b=-1，则可得
∴在(a+b)n的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和
题型一　二项式系数和与各项的系数和的基本问题
由题意知2n＝32，得n＝5.令x＝1，可得展开式中各项系数的和为(3×12－1)5＝32.
(1)当x＝1时，等号左边为(1－2)7＝－1，等号右边为a0＋a1＋a2＋…＋a7，∴a0＋a1＋a2＋…＋a7＝－1.当x＝0时，a0＝1.∴a1＋a2＋…＋a7＝－1－1＝－2.
(2)令x＝1，得a0＋a1＋a2＋…＋a7＝－1，①令x＝－1，得a0－a1＋a2－a3＋a4－a5＋a6－a7＝37，②①－②，得2(a1＋a3＋a5＋a7)＝－1－37，
(3)由展开式，知a1，a3，a5，a7均为负数，a0，a2，a4，a6均为正数，
∴|a0|＋|a1|＋…＋|a7|＝a0－a1＋a2－a3＋a4－a5＋a6－a7.
由(2)可知，a0－a1＋a2－a3＋a4－a5＋a6－a7＝37，
∴|a0|＋|a1|＋…＋|a7|＝37＝2 187.
对于(a＋bx)n＝a0＋a1x＋a2x2＋…＋anxn的展开式，求各项系数和时，可令x＝1，得a0＋a1＋a2＋…＋an＝(a＋b)n.若求奇数项和或偶数项和，可分别令x＝1和x＝－1，
两式相加减即可求出结果．对于形如(ax2＋bx＋c)n的式子，求其展开式的各项系数和，只需令x＝1.对于(ax＋by)n(a，b为常数)的式子，求其展开式的各项系数和，可令x＝y＝1.
多项式x3＋x10＝a0＋a1(x＋1)＋…＋a9(x＋1)9＋a10(x＋1)10.(1)求a0＋a1＋…＋a9＋a10的值；(2)求a0－a1＋a2－a3＋…－a9＋a10的值；(3)求a0.
(1)令x＋1＝1，即x＝0，得0＝a0＋a1×1＋…＋a9×19＋a10×110，即a0＋a1＋…＋a9＋a10＝0.
(2)令x＋1＝－1，即x＝－2，得(－2)3＋(－2)10＝a0－a1＋a2－a3＋…－a9＋a10，即a0－a1＋a2－a3＋…－a9＋a10＝1 016.
(3)令x＋1＝0，即x＝－1，得a0＝0.
题型二　系数最大项问题
例2　设m为正整数，(x＋y)2m展开式的二项式系数的最大值为a，(x＋y)2m＋1展开式的二项式系数的最大值为b，若13a＝7b，则m＝(　　)A．5 B．6 C．7 D．8
所以展开式中第5项的二项式系数最大，
解得7≤r≤8，所以展开式中系数最大的项为第8项或第9项，即T8＝
(2021·春季高考上海卷)已知(1＋x)n的展开式中，唯有x3的系数最大，则(1＋x)n的系数和为________．
解得5＜n＜7，又n∈N，因此n＝6.
设(1＋x)6＝a0x6＋a1x5＋a2x4＋…＋a5x＋a6，令x＝1，则(1＋x)6的系数和为a0＋a1＋a2＋…＋a6＝26＝64.
题型三　关于整除或余数问题
(1)证明：32n＋3－24n＋37能被64整除．(2)求9192被100除所得的余数．
(1)32n＋3－24n＋37＝3×9n＋1－24n＋37＝3(8＋1)n＋1－24n＋37
显然上式是64的倍数，故原式能被64整除．
因为展开式中前92项均能被100整除，所以只需求最后一项除以100的余数．
前91项均能被100整除，后两项和为－919.因余数为正，可从前面的数中分离出1 000，结果为1 000－919＝81，故9192被100除所得的余数为81.
整除或求余数问题的求解策略(1)用二项式定理处理整除问题，通常把幂的底数写成除数(或与除数密切关联的数)与某数的和或差的形式，再利用二项式定理展开，只考虑后面一、二项(或者是某些项)就可以了．(2)要注意余数的范围，对给定的整数a，b(b≠0)，有确定的一对整数q和r，满足a＝bq＋r，其中b为除数，r为余数，r∈[0，|b|)，利用二项式定理展开变形后，若剩余部分是负数，要注意转换成正数．　
1．211除以9的余数为________．
2.今天是星期四，那么8100天后的这一天是星期几？
8100=(7+1)100=
＝7( )+1
余数是1，所以是星期五