初中数学人教版七年级下册第五章 相交线与平行线综合与测试综合训练题
展开2021年度人教版七年级数学下册第5章相交线与平行线章末综合优生辅导训练
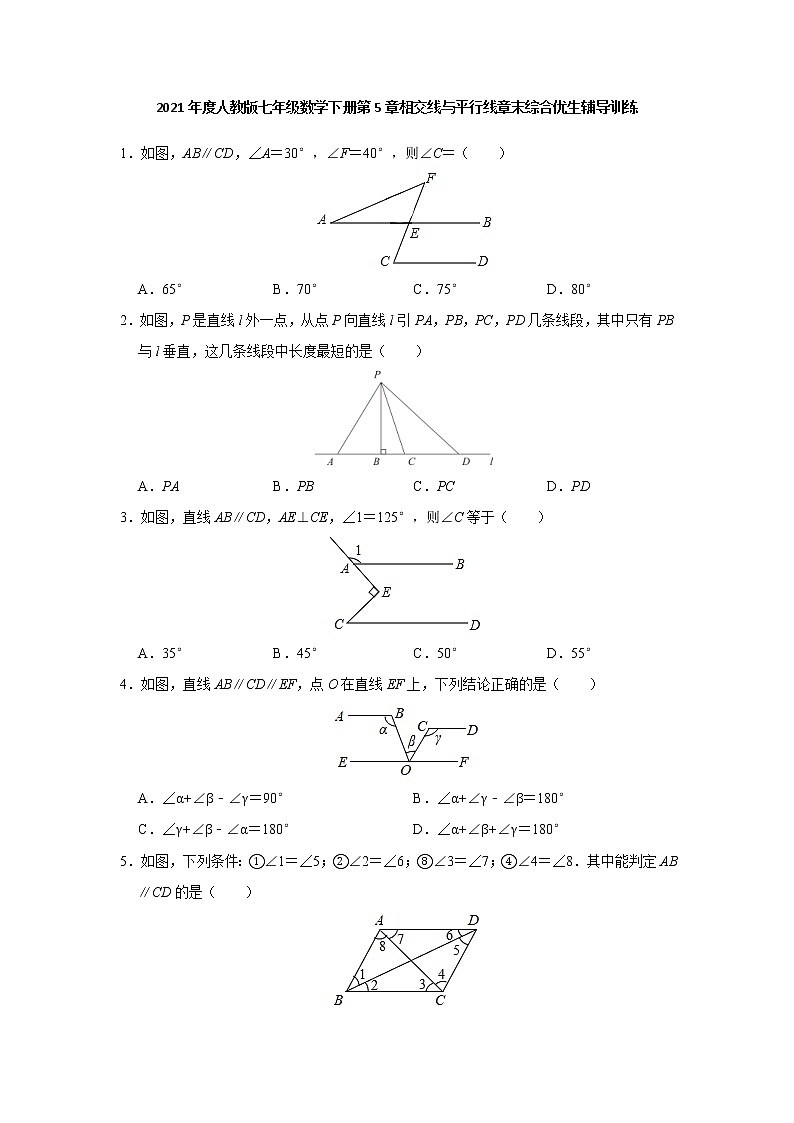
1.如图,AB∥CD,∠A=30°,∠F=40°,则∠C=( )
A.65° B.70° C.75° D.80°
2.如图,P是直线l外一点,从点P向直线l引PA,PB,PC,PD几条线段,其中只有PB与l垂直,这几条线段中长度最短的是( )
A.PA B.PB C.PC D.PD
3.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
4.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
5.如图,下列条件:①∠1=∠5;②∠2=∠6;⑧∠3=∠7;④∠4=∠8.其中能判定AB∥CD的是( )
A.①② B.②③ C.①④ D.②④
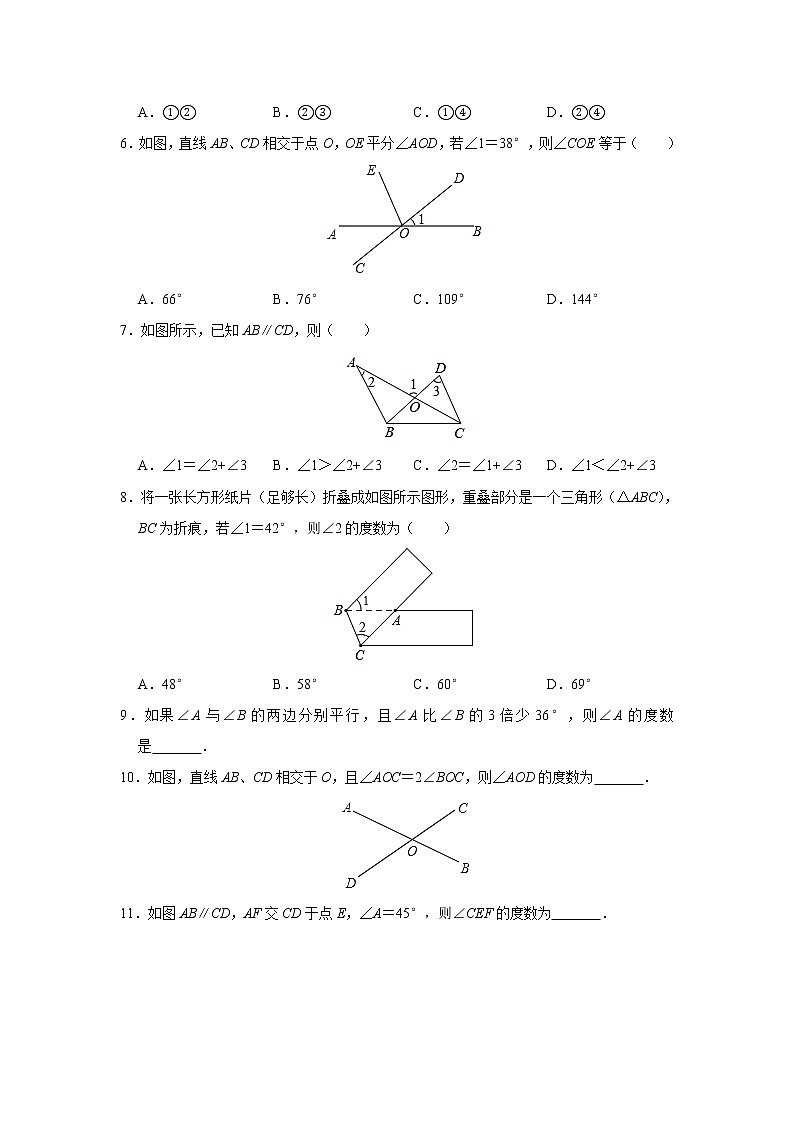
6.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠1=38°,则∠COE等于( )
A.66° B.76° C.109° D.144°
7.如图所示,已知AB∥CD,则( )
A.∠1=∠2+∠3 B.∠1>∠2+∠3 C.∠2=∠1+∠3 D.∠1<∠2+∠3
8.将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
9.如果∠A与∠B的两边分别平行,且∠A比∠B的3倍少36°,则∠A的度数是 .
10.如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为 .
11.如图AB∥CD,AF交CD于点E,∠A=45°,则∠CEF的度数为 .
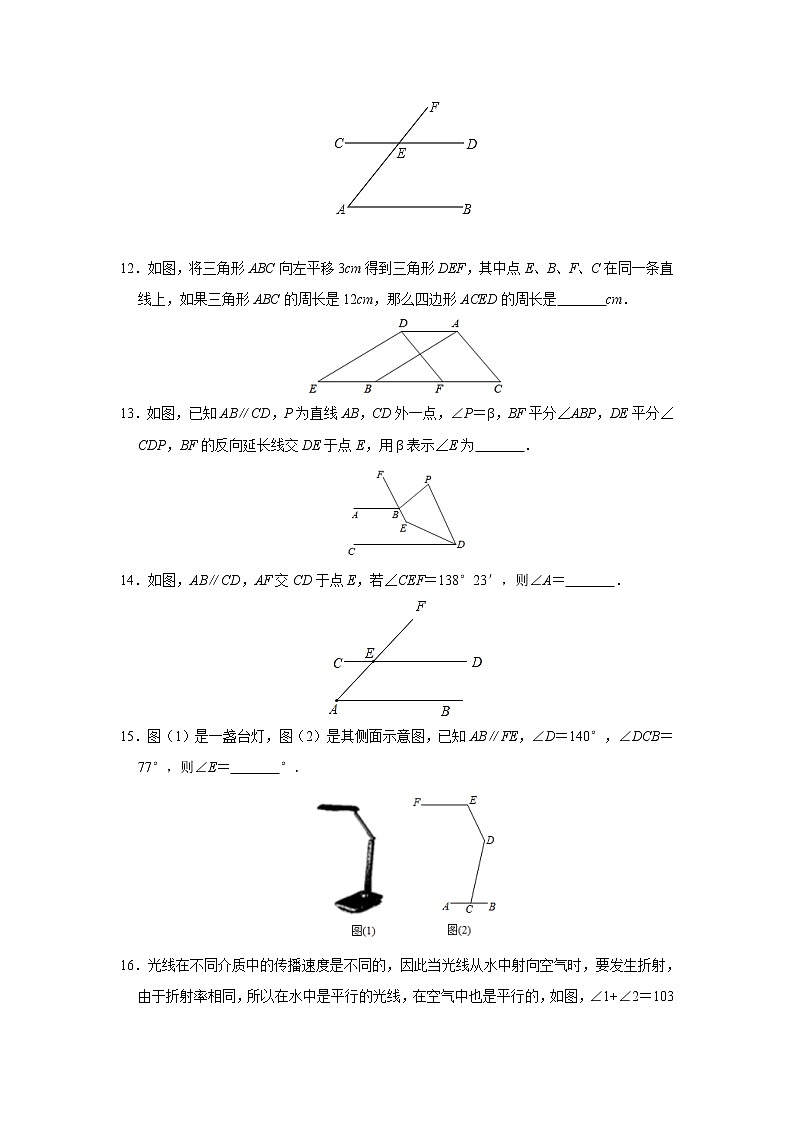
12.如图,将三角形ABC向左平移3cm得到三角形DEF,其中点E、B、F、C在同一条直线上,如果三角形ABC的周长是12cm,那么四边形ACED的周长是 cm.
13.如图,已知AB∥CD,P为直线AB,CD外一点,∠P=β,BF平分∠ABP,DE平分∠CDP,BF的反向延长线交DE于点E,用β表示∠E为 .
14.如图,AB∥CD,AF交CD于点E,若∠CEF=138°23′,则∠A= .
15.图(1)是一盏台灯,图(2)是其侧面示意图,已知AB∥FE,∠D=140°,∠DCB=77°,则∠E= °.
16.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,∠1+∠2=103°,则∠3﹣∠4的度数为 .
17.如图,已知AB∥CD,∠BAD和∠BCD的平分线交于点E,∠1=100°,∠BAD=m°,则∠AEC的度数为 .
18.将长度为5cm的线段向上平移3cm后所得线段的长度为 .
19.如图,△DCF是Rt△ABC沿着BC平移得到的,如果AB=12cm,BE=5cm,DH=4cm,则图中阴影部分的面积为 cm2.
20.如图,这是购物车的侧面示意图,扶手AB与车底CD平行,∠1=100°,∠2=50°,则∠3的度数是 .
21.如图,在△ABC中,点D、E分别在AB、BC上,且DE∥AC,∠1=∠2,
(1)AF与BC的位置关系是 ;
(2)如果∠B=30°,且∠2=80°,那么∠BAC= .
22.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
23.如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:AC∥DF.
24.如图,直线AB和直线BC相交于点B,连接AC,点D、E、H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°
(1)求证:∠CEF=∠EAD;
(2)若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).
25.如图,已知∠1+∠2=180°,∠3=∠B,
(1)证明:EF∥AB.
(2)试判断∠AED与∠C的大小关系,并说明你的理由.
26.如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.
(1)求∠DOB的度数;
(2)OF是∠AOD的角平分线吗?为什么?
27.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
28.如图,AB∥CD,定点E,F分别在直线AB,CD上,平行线AB,CD之间有一动点P.
(1)如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为 ,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为 .
(2)如图3,当∠EPF=90°,FP平分∠EFC时,求证:EP平分∠AEF;
(3)如图4,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF= ;
②猜想∠EPF与∠EQF的数量关系,并说明理由.
参考答案
1.解:∵∠A=30°,∠F=40°,
∴∠FEB=∠A+∠F=30°+40°=70°,
∵AB∥CD,
∴∠C=∠FEB=70°,
故选:B.www.czsx.com.cn
2.解:直线外一点P与直线l上各点连接的所有线段中,最短的是PB,依据是垂线段最短,
故选:B.
3.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠BAE=∠AEF.
∵EF∥CD,
∴∠C=∠CEF.
∵AE⊥CE,
∴∠AEC=90°,即∠AEF+∠CEF=90°,
∴∠BAE+∠C=90°.
∵∠1=125°,∠1+∠BAE=180°,
∴∠BAE=180°﹣125°=55°,
∴∠C=90°﹣55°=35°.
故选:A.
4.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
5.解:①∵∠1=∠5,
∴AB∥CD,能判定AB∥CD;
②∵∠2=∠6,
∴AD∥BC,不能判定AB∥CD;
③∵∠3=∠7;
∴AD∥BC,不能判定AB∥CD;
④∵∠4=∠8,
∴AB∥CD,能判定AB∥CD.
故选:C.
6.解:∵∠1=38°,
∴∠AOD=180°﹣∠1=142°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=71°,
∴∠COE=180°﹣∠DOE=109°,
故选:C.
7.解:∵AB∥CD,
∴∠2=∠4,
∵∠1=∠3+∠4,
∴∠1=∠3+∠2,
故选:A.
8.解:如右图所示,
∵长方形的两条长边平行,∠1=42°,
∴∠1=∠4=42°,∠4=∠5,
∴∠5=42°,
由折叠的性质可知,∠2=∠3,
∵∠2+∠3+∠5=180°,
∴∠2=69°,
故选:D.
9.解:∵∠A与∠B的两边分别平行,
∴∠A与∠B相等或互补.
分两种情况:
①当∠A+∠B=180°时,∠A=3∠B﹣36°,
解得:∠A=126°;
②当∠A=∠B,∠A=3∠B﹣36°,
解得:∠A=18°.
所以∠A=18°或126°.
故答案为18°或126°.
10.解:∵∠AOC+∠BOC=180°,
又已知∠AOC=2∠BOC,
∴3∠BOC=180°,
解得∠BOC=60°,
∴∠AOD=∠BOC=60°.
11.解:∵AB∥CD,∠A=45°,
∴∠AEC=∠A=45°,
∵∠CEF+∠AEC=180°,
∴∠CEF=180°﹣∠AEC=180°﹣45°=135°,
故答案为:135°.
12.解:∵将三角形ABC向左平移3cm得到三角形DEF,
∴AD=EB=3cm,△ABC≌△DEF,则ED=AB,EF=BC,DF=AC,
∵三角形ABC的周长是12cm,
∴△DEF的周长是12cm,
∴DE+DF+EF=DE+AC+BC=12cm,
∴四边形ACED的周长是:AD+BE+BC+AC+DE=3+3+12=18(cm).
故答案为:18.
13.解:延长AB交PD于点G,延长FE交CD于点H,
∵BF平分∠ABP,DE平分∠CDP,
∴∠1=∠2,∠3=∠4,
∵AB∥CD,
∴∠1=∠5,∠6=∠PDC=2∠3,
∵∠PBG=180°﹣2∠1,
∴∠PBG=180°﹣2∠5,
∴∠5=90°﹣∠PBG,
∵∠FED=180°﹣∠HED,∠5=180°﹣∠EHD,∠EHD+∠HED+∠3=180°,
∴180°﹣∠5+180°﹣∠FED+∠3=180°,
∴∠FED=180°﹣∠5+∠3,
∴∠FED=180°﹣(90°﹣∠PBG)+∠6=90°+(∠PBG+∠6)=90°+(180°﹣∠P)=180°﹣∠P,
∵∠P=β,
∴∠FED=180°﹣β,
故答案为:180°﹣β.
14.解:∵∠CEF=138°23′,
∴∠FED=180°﹣∠CEF=180°﹣138°23′=41°37′,
∵AB∥CD,
∴∠A=∠FED=41°37′,
故答案为:41°37′.
15.解:过点D作DH∥EF,如右图所示,
∵AB∥FE,DH∥EF,
∴AB∥DH∥EF,
∴∠FED+∠1=180°,∠2=∠DCB,
∵∠DCB=77°,
∴∠2=77°,
∵∠EDC=140°,
∴∠1=140°﹣∠2=140°﹣77°=63°,
∴∠FED=180°﹣63°=117°,
故答案为:117.
16.解:如图,∵AB∥CD,
∴∠5=180°﹣∠2,
∵AC∥BD,
∴∠3=∠5,
∵AE∥BF,
∴∠1=∠6,
∵EF∥AB,
∴∠4=∠6,
∴∠3﹣∠4=180°﹣∠2﹣∠1=180°﹣(∠1+∠2)=77°.
故答案为:77°.
17.解:如图,过点E作EF∥AB,
∵AB∥CD,EF∥AB,
∴AB∥EF∥CD,
∴∠BAE=∠AEF,∠FEC=∠ECD,∠1+∠BCD=180°,
∴∠BCD=180°﹣∠1=180°﹣100°=80°,
∵∠BAD和∠BCD的平分线交于点E,
∴∠BAE=∠BAD=,∠ECD=∠BCD=40°,
∴∠AEC=∠AEF+∠FEC=∠BAE+∠ECD=40°+,
故答案为:40°+.
18.解:线段长度不变,还是5cm.
故答案为5cm.
19.解:∵△DCF是Rt△ABC沿着BC平移得到,
∴△ABC≌△DEF,DE=AB=12,
∵DH=4,
∴HE=12﹣4=8,
∴S△ABC=S△DEF,
∴图中阴影部分的面积=S梯形ABEH=×(8+12)×5=50(cm2).
故答案为50.
20.解:∵AB∥CD,
∴∠1=∠CDA=100°,
∵∠2=50°,
∴∠3=50°.
故答案为:50°.
21.解:(1)∵DE∥AC,
∴∠2=∠C,
∵∠1=∠2,
∴∠1=∠C,
∴AF∥BC;
(2)∵AF∥BC,
∴∠B+∠BAF=180°,
∴∠BAF=180°﹣30°=150°,
∵∠1=∠2=80°,
∴∠BAC=150°﹣80°=70°.
故答案为平行;70°.
22.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
23.证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
24.解:(1)∵∠3+∠DFE=180°,∠1+∠3=180°
∴∠DFE=∠1,
∴AB∥EF,
∴∠CEF=∠EAD;
(2)∵AB∥EF,
∴∠2+∠BDE=180°
又∵∠2=α
∴∠BDE=180°﹣α
又∵DH平 分∠BDE
∴∠1=∠BDE=(180°﹣α)
∴∠3=180°﹣(180°﹣α)=90°+α
25.解:(1)∵∠1+∠DFE=180°(平角定义),∠1+∠2=180°(已知),
∴∠2=∠DFE,
∴EF∥AB(内错角相等,两直线平行);
(2)∠AED与∠C相等.
∵EF∥AB,
∴∠3=∠ADE(两直线平行,内错角相等),
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠C(两直线平行,同位角相等).
26.解:(1)∵OE平分∠AOC,
∴∠AOC=2∠AOE=64°,
∵∠DOB与∠AOC是对顶角,
∴∠DOB=∠AOC=64°;
(2)∵OE⊥OF,
∴∠EOF=90°,
∴∠AOF=∠EOF﹣∠AOE=58°,
∵∠AOD=180°﹣∠AOC=116°,
∴∠AOD=2∠AOF,
∴OF是∠AOD的角平分线.
27.(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+60°,∠CBD=70°,
∴∠3=25°,
∵AB∥CD,
∴∠C=∠3=25°.
28.解:(1)如图1,过点P作PG∥AB,
∵PG∥AB,
∴∠EPG=∠AEP,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠PFC,
∴∠AEP+∠PFC=∠EPF;
如图2,当P点在EF的右侧时,过点P作PG∥AB,
∵PG∥AB,
∴∠EPG+∠AEP=180,
∵AB∥CD,
∴PG∥CD,
∴∠FPG+∠PFC=180°,
∴∠AEP+∠PFC+∠EPG+∠FPG=360°,
∴∠AEP+∠EPF+∠PFC=360°;
故答案为:∠AEP+∠PFC=∠EPF,∠AEP+∠EPF+∠PFC=360°;
(2)∵AB∥CD,
∴∠AEF+∠EFC=180°,
∵∠EPF=90°,
∴∠PEF+∠EFP=90°,
∴∠PEA+∠CFP=90°,
∵FP平分∠EFC,
∴∠EFP=∠CFP,
∴∠PEF=∠PEA,
∴EP平分∠AEF;
(3)①∵∠EPF=60°,
∴∠PEB+∠PFD=360°﹣60°=300°,
∵EQ,FQ分别平分∠PEB和∠PFD,
∴∠BEQ=∠PEB,∠QFD=∠PFD,
∴∠EQF=∠BEQ+∠QFD= (∠PEB+∠PFD)=×300°=150°;
故答案为:150°;
②∵EQ,FQ分别平分∠PEB和∠PFD,
∴∠BEQ=∠PEB,∠QFD=∠PFD,
则∠EPF=180°﹣2∠BEQ+180°﹣2∠DFQ=360°﹣2(∠BEQ+∠PFD),
∵∠EQF=∠BEQ+∠DFQ,
∴∠EPF+2∠EQF=360°
《第1章整式的乘除》期末综合复习优生辅导训练(附答案)2020-2021学年七年级数学北师大版下册: 这是一份《第1章整式的乘除》期末综合复习优生辅导训练(附答案)2020-2021学年七年级数学北师大版下册,共7页。试卷主要包含了下列计算中,正确的是,计算等内容,欢迎下载使用。
2020-2021学年七年级数学浙教版下册《第1章平行线》期中复习优生辅导训练(附答案): 这是一份2020-2021学年七年级数学浙教版下册《第1章平行线》期中复习优生辅导训练(附答案),共21页。
2020-2021学年七年级数学浙教版下册《第3章整式的乘除》期中复习优生辅导训练(附答案): 这是一份2020-2021学年七年级数学浙教版下册《第3章整式的乘除》期中复习优生辅导训练(附答案),共11页。试卷主要包含了小颖用4张长为a,宽为b,小淇将,计算,如图1的8张宽为a,长为b,若a2+4a=5,则代数式2a等内容,欢迎下载使用。













