2021-2022学年天津市南开区八年级（下）期末数学试卷（含解析）

2021-2022学年天津市南开区八年级（下）期末数学试卷

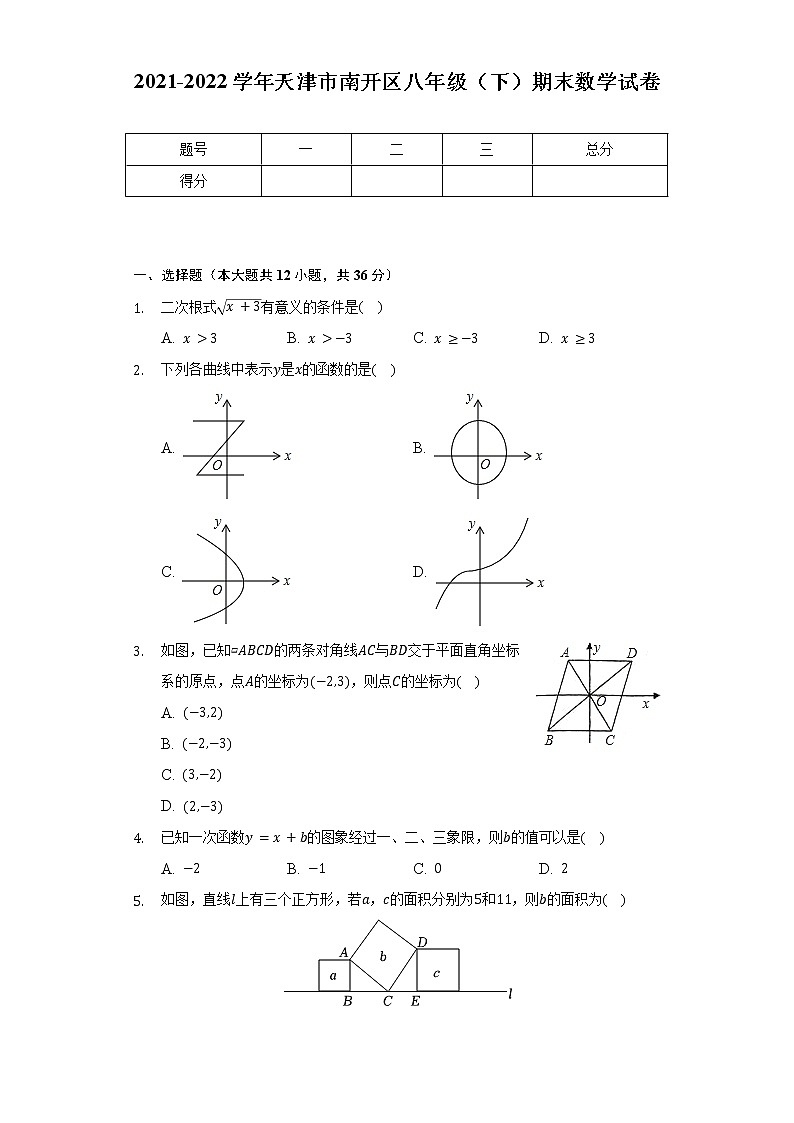
一、选择题（本大题共12小题，共36分）

1. 二次根式有意义的条件是(    )

A.  B.  C.  D.

2. 下列各曲线中表示是的函数的是(    )

A.  B.
C.  D.

3. 如图，已知▱的两条对角线与交于平面直角坐标系的原点，点的坐标为，则点的坐标为(    )

A.
B.
C.
D.

4. 已知一次函数的图象经过一、二、三象限，则的值可以是(    )

A.  B.  C.  D.

5. 如图，直线上有三个正方形，若，的面积分别为和，则的面积为(    )

A.  B.  C.  D.

6. 将直线向右平移个单位所得的直线的解析式是(    )

A.  B.  C.  D.

7. 下列条件中，不能判断一个三角形是直角三角形的是(    )

A. 三个角的比是：：
B. 三条边，，满足关系
C. 三条边的比是：：
D. 三边长为，，

8. 年北京张家口举办了冬季奥运会，很多学校也开设了相关的课程．下表记录了某校名同学短道速滑选拔赛成绩的平均数与方差．

据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择(    )

A. 队员 B. 队员 C. 队员 D. 队员

9. 如图，在菱形中，，，则菱形边上的高的长是(    )

A.
B.
C.
D.

10. 一次函数与 的图象如图，则下列结论；；当 时，中，正确的个数是(    )

A.  B.  C.  D.

11. 如图，在矩形中，，，点是边上靠近点的三等分点，动点从点出发，沿路径运动，则的面积与点经过的路径长之间的函数关系用图象表示大致是(    )

A.  B.
C.  D.

12. 如图，在平面直角坐标系中，，两点坐标分别为，，为线段上的一动点，以，为边构造平行四边形，则使对角线值最小的点的坐标为(    )

A.
B.
C.
D.

二、填空题（本大题共6小题，共18分）

13. 化简：______．
14. 为监测某河道水质，进行了次水质检测，绘制了如图的氨氮含量的折线统计图．若这次水质检测氨氮含量平均数为，则第次检测得到的氨氮含量是______ ．

15. 九章算术是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．在九章算术中的勾股卷中有这样一道题：今有竹高一丈，末折抵底，去本三尺．折者高几何？意思为：一根竹子，原高一丈，虫伤有病，一阵风将竹子折断，其竹稍恰好抵地，抵地处离远处竹子三尺远，则原处还有______尺竹子．请直接写出答案，注：丈尺．
16. 如图，将一张矩形纸片沿折叠后，点落在边上的点处，点落在点处．若，则图中的度数为______．

17. 若函数是关于的一次函数，______．
18. 已知：正方形的边长为，点、分别在、上，，与相交于点，点为的中点，连接，则的长为______．

三、解答题（本大题共6小题，共46分）

19. 计算
    Ⅰ；
    Ⅱ．
20. 某高校学生会向全校名学生发起了“爱心一日捐”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图和图，请根据相关信息，解答下列问题：
    本次接受随机抽样调查的学生人数为______ ，图中的值是______ ；
    求本次你调查获取的样本数据的平均数、众数和中位数；
    根据样本数据，估计该校本次活动捐款金额为元的学生人数．

21. 如图，等边的边长是，、分别为、的中点，延长至点，使，连接和．
    求证：四边形是平行四边形；
    求的长．

22. 如图，点是菱形对角线的交点，，，连接．
    Ⅰ求证：；
    Ⅱ如果，，求四边形的周长．

23. 工厂某车间需加工一批零件，甲组工人加工中因故停产检修机器一次，然后以原来的工作效率继续加工，由于时间紧任务重，乙组工人也加入共同加工零件．设甲组加工时间为时，甲组加工零件的数量为个，乙组加工零件的数量为个，其函数图象如图所示．
    Ⅰ填空：
    ______；
    甲组工人每小时加工零件______个；
    乙组工人每小时加工零件______个；
    甲组加工______小时的时候，甲、乙两组加工零件的总数为个．
    Ⅱ直接写出，与之间的函数关系式．

24. 如图，在平面直角坐标系中，为坐标原点，矩形的顶点，，将矩形的一个角沿直线折叠，使得点落在对角线上的点处，折痕与轴交于点，
    Ⅰ线段的长度为______；
    Ⅱ求线段的长，以及直线所对应的函数表达式；
    Ⅲ若点为该平面内一点，且使得，直接写出满足条件的直线的解析式．

答案和解析

1.【答案】 

【解析】解：要使有意义，必须，
，
故选：．
根据二次根式有意义的条件求出，求出即可．
本题考查了二次根式有意义的条件的应用，注意：要使有意义，必须．
 

2.【答案】 

【解析】解：根据函数的意义可知：对于自变量的任何值，都有唯一的值与之相对应，故D正确．
故选：．
根据函数的意义求解即可求出答案．
主要考查了函数的定义．注意函数的意义反映在图象上简单的判断方法是：做垂直轴的直线在左右平移的过程中与函数图象只会有一个交点．
 

3.【答案】 

【解析】解：在平行四边形中，点与点关于原点对称
点坐标为．
故选D．
根据平行四边形是中心对称的特点可知，点与点关于原点对称，所以的坐标为．
主要考查了平行四边形的性质和坐标与图形的关系．要会根据平行四边形的性质得到点与点关于原点对称的特点，是解题的关键．
 

4.【答案】 

【解析】

【分析】
本题考查了一次函数图象与系数的关系：一次函数、为常数，是一条直线，当，图象经过第一、三象限，随的增大而增大；当，图象经过第二、四象限，随的增大而减小；图象与轴的交点坐标为根据一次函数图象与系数的关系得到，，然后对选项进行判断．
【解答】
解：一次函数的图象经过一、二、三象限，
，
各选项中只有符合题意．
故选D．  

5.【答案】 

【解析】解：根据题意，得，，
，，
，
在和中，
，
≌，
，，
，的面积分别为和，
，，
，
根据勾股定理，得，
的面积为，
故选：．
根据正方形的性质，易证≌，可得，，根据，的面积以及勾股定理即可求出的面积．
本题考查了全等三角形的判定和性质，涉及正方形的性质，勾股定理等，熟练掌握全等三角形的判定方法是解题的关键．
 

6.【答案】 

【解析】解：根据题意，得直线向右平移个单位，
即对应点的纵坐标不变，横坐标减，
所以得到的解析式是．
故选：．
根据平移性质可由已知的解析式写出新的解析式．
本题考查一次函数的图象与几何变换，正比例函数的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

7.【答案】 

【解析】解：、三个角的比是：：，可得最大角，是直角三角形，不符合题意；
B、三条边，，满足关系，可得：，是直角三角形，不符合题意；
C、三条边的比是：：，，不是直角三角形，符合题意；
D、，是直角三角形，不符合题意；
故选：．
根据直角三角形的判定方法，对选项进行一一分析，排除错误答案．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可；若已知角，只要求得一个角为即可．
 

8.【答案】 

【解析】解：因为队员和队员的平均成绩比队员和队员好，
所以从队员和队员选其中一人参加，
又因为队员的方差比队员的方差小，
所以要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择队员．
故选：．
先比较平均数，再比较方差即可．
本题主要考查方差，解题的关键是掌握方差的意义：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
 

9.【答案】 

【解析】解：对角线，交于点，则为直角三角形
则，
，
菱形的面积根据边长和高可以计算，根据对角线长也可以计算，
即，
解得：，
故选：．
对角线，交于点，则为直角三角形，在中，已知，根据勾股定理即可求得的长，根据菱形面积不同的计算方法可以求得的长度，即可解题．
本题考查了菱形面积的计算方法，考查了勾股定理在直角三角形中的运用，本题中根据勾股定理计算的值是解题的关键．
 

10.【答案】 

【解析】

【分析】
本题考查了两条直线相交问题，难点在于根据函数图象的走势和与轴的交点来判断各个函数，的值．根据和的图象可知：，，所以当时，相应的的值，图象均高于的图象．
【解答】
解：的函数值随的增大而减小，
；故正确
的图象与轴交于负半轴，
；
当时，相应的的值，图象均高于的图象，
，故错误．
故选B．  

11.【答案】 

【解析】解：在矩形中，，，
，，
点是边上靠近点的三等分点，
，
点在上时，的面积，
点在上时，，
，
，
，
，
点在上时，，
，
故选：．
求出的长，然后分点在上时，利用三角形的面积公式列式得到与的函数关系；点在上时，根据列式整理得到与的关系式；点在上时，利用三角形的面积公式列式得到与的关系式，然后选择答案即可．
本题考查了动点问题函数图象，读懂题目信息，根据点的位置的不同分三段列式求出与的关系式是解题的关键．
 

12.【答案】 

【解析】解：由端点分别在两条平行线上的所有线段中，垂直于平行线的线段最短，
当时，最短，
，，
，
，
四边形是平行四边形，
，
，
，，，
四边形是矩形，
，
．
故选：．
由端点分别在两条平行线上的所有线段中，垂直于平行线的线段最短，当时，最短，易证，由平行四边形的性质得出，，由，则四边形是矩形，即可得出结果，
本题考查了平行线之间的距离、垂线段最短、平行四边形的性质、平行线的判定、矩形的判定与性质等知识；正确判断出当时，最短是解题的关键．
 

13.【答案】 

【解析】解：．
故答案为．
根据算术平方根的定义：一个非负数的正的平方根，即为这个数的算术平方根．所以结果必须为正数，而的平方根为，所以算术平方根为．
他主要考查了算术平方根的定义，注意算术平方根的概念易与平方根的概念混淆而导致错误．规律总结：弄清概念是解决本题的关键．
 

14.【答案】 

【解析】解：由题意可得，
第次检测得到的氨氮含量是：，
故答案为：．
根据题意可以求得这次总的含量，由折线统计图可以得到除第次的含量，从而可以得到第次检测得到的氨氮含量．
本题考查算术平均数、折线统计图，解题的关键是明确题意，找出所求问题需要的条件．
 

15.【答案】 

【解析】解：设竹子折断处离地面尺，则斜边为尺，
根据勾股定理得：，
解得：．
故答案为：．
竹子折断后刚好构成一直角三角形，设竹子折断处离地面尺，则斜边为尺．利用勾股定理解题即可．
此题考查了勾股定理的应用，解题的关键是利用题目信息构造直角三角形，从而运用勾股定理解题．
 

16.【答案】 

【解析】解：，
，
由翻折可得：，
，
故答案为：
根据平行线的性质和翻折的性质解答即可．
此题考查平行线的性质，关键是根据平行线的性质和翻折的性质解答．
 

17.【答案】或或 

【解析】解：函数是关于的一次函数，
，，
解得：；
或，
解得：；
或，
解得：．
故答案为：或或．
由一次函数的定义可知，或或，从而可求得的值．
本题主要考查的是一次函数的定义，掌握一次函数的定义是解题的关键．
 

18.【答案】 

【解析】解：四边形为正方形，
，，
，，
≌，
，
，
，
，
点为的中点，
，
，


故答案为：
根据正方形的四条边都相等可得，每一个角都是直角可得，然后利用“边角边”证明≌得，进一步得，从而知，利用勾股定理求出的长即可得出答案．
本题考查了正方形的性质，全等三角形的判定与性质，直角三角形两锐角互余等知识，掌握三角形全等的判定方法与正方形的性质是解题的关键．
 

19.【答案】解：原式

；

原式

． 

【解析】先根据二次根式的性质进行计算，再算乘法，最后合并同类二次根式即可；
先根据平方差公式，完全平方公式和二次根式的性质进行计算，再根据二次根式的加减进行计算即可．
本题考查了二次根式的混合运算，能正确运用二次根式的运算法则进行计算是解此题的关键，注意运算顺序．
 

20.【答案】； 

【解析】解：调查的学生数是：人，
．
故答案是：，；
平均数是：元，众数是：元，中位数是：元；
该校本次活动捐款金额为元的学生人数是：人．
根据捐款数是元的，所占的百分比是，即可求得总人数，然后根据百分比的意义求得的值；
根据平均数、众数、中位数的定义即可求解；
利用总人数乘以对应的百分比即可求解．
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
 

21.【答案】证明：、分别为、的中点，
为的中位线，
，
延长至点，使，
，，
四边形是平行四边形．

解：，
四边形是平行四边形，
，
为的中点，等边的边长是，
，，，
． 

【解析】直接利用三角形中位线定理得出，，进而得出；
利用平行四边形的判定与性质得出，进而利用等边三角形的性质以及勾股定理得出的长．
此题主要考查了等边三角形的性质以及平行四边形的判定与性质和三角形中位线定理、勾股定理等知识，得出，是解题关键．
 

22.【答案】Ⅰ证明：点是菱形对角线的交点，
，
，
，，
四边形为平行四边形，
而，
四边形为矩形，
；
Ⅱ解：点是菱形对角线的交点，
，，，
，
在中，，
，
四边形的周长． 

【解析】Ⅰ先根据菱形的性质得到，再证明四边形为平行四边形，则可判定四边形为矩形，然后根据矩形的性质得到结论；
Ⅱ先根据菱形的性质得到，，，则利用勾股定理计算出，则，然后计算矩形的周长即可．
本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了矩形的判定与性质．
 

23.【答案】       

【解析】解：Ⅰ根据函数图象中的数据，时，甲组加工零件的数量为个，
时，甲组加工零件的数量为个，
甲组工人每小时加工零件：个，
个；
根据函数图象中的数据，甲组工人每小时加工零件：个；
根据函数图象中的数据，乙组工人每小时加工零件：个；
设甲组加工小时时，甲、乙两组加工零件的总数为个，
由题意得：，
解得，
即甲组加工小时时，甲、乙两组加工零件的总数为个．
故答案为：；；；．
Ⅱ设与之间的函数关系式是，
，
解得：，
即与之间的函数关系式是；
时，，
时，，
时，设，
，
解得：，
，
．
Ⅰ根据函数图象中的数据，可以直接得，时甲组加工零件的数量，可得到甲的速度，然后即可计算出的值；
根据函数图象中的数据，可得到甲的速度；
根据函数图象中的数据，可得乙组工人的速度；
根据题意，可以列出相应的方程，然后即可得到甲组加工多长时间时，甲、乙两组加工零件的总数为个；
Ⅱ根据函数图象中的数据，可以得到、与之间的函数关系式，注意的取值范围．
本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．
 

24.【答案】 

【解析】解：，，
，，
矩形，
，
在中，，
故答案为：；
由折叠可知，，，
，
，
，
，
在中，，
解得，
，，
，
，，
，
设直线的解析式为，
，
解得，
；
取点，过点作轴交于点，
连接，过点作交轴于点，过点作交于点，
，，
，
，
，
，
，
，
，
设直线与轴交于点时，，
，
，
，
，
设直线的解析式为，
，
解得，
；
设直线与轴交于点时，，
，
，
，
，
，
解得，
；
综上所述：直线的解析式为或．
矩形中，可得；
求出点，，由待定系数法求出直线的解析式；
取点，过点作轴交于点，连接，过点作交轴于点，过点作交于点，通过构造直角三角形可得，设直线与轴交于点时，求出，可求直线的解析式为；设直线与轴交于点时，求出，可求直线的解析式为．
本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，熟练掌握待定系数法求函数解析式的方法，直角三角形的性质是解题的关键．