数学选择性必修 第一册1.2 空间向量基本定理课文ppt课件

这是一份数学选择性必修 第一册1.2 空间向量基本定理课文ppt课件，共15页。PPT课件主要包含了平面向量基本定理，三个向量共面不可以，空间向量基本定理等内容，欢迎下载使用。

　　如果 e1，e2是同一平面内的两个不共线向量，那么对于这一平面内的任一向量 a，有且只有一对实数 λ1，λ2，使 a＝λ1e1＋λ2e2． 若 e1，e2不共线，我们把{e1，e2}叫做表示这一平面内所有向量的一个基底．
空间中的任意向量能不能通过有限个向量的线性运算来表示呢？
为了表示空间中的任意向量，我们至少需要几个向量？
两个不共线的向量还够用吗？
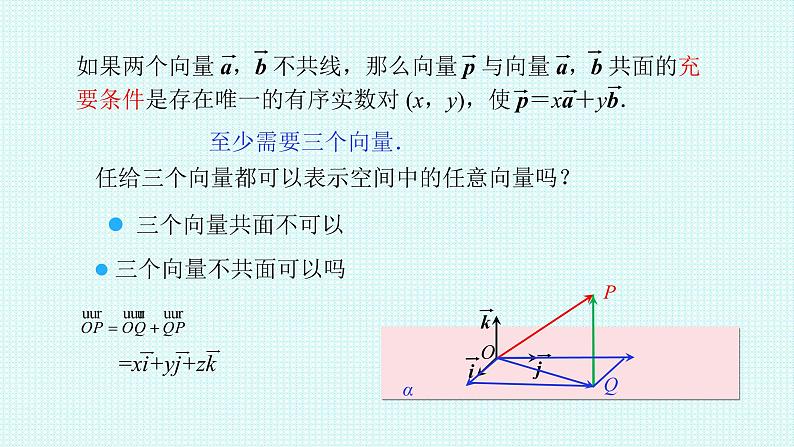
如果两个向量 a，b 不共线，那么向量 p 与向量 a，b 共面的充要条件是存在唯一的有序实数对 (x，y)，使 p＝xa＋yb．
任给三个向量都可以表示空间中的任意向量吗？
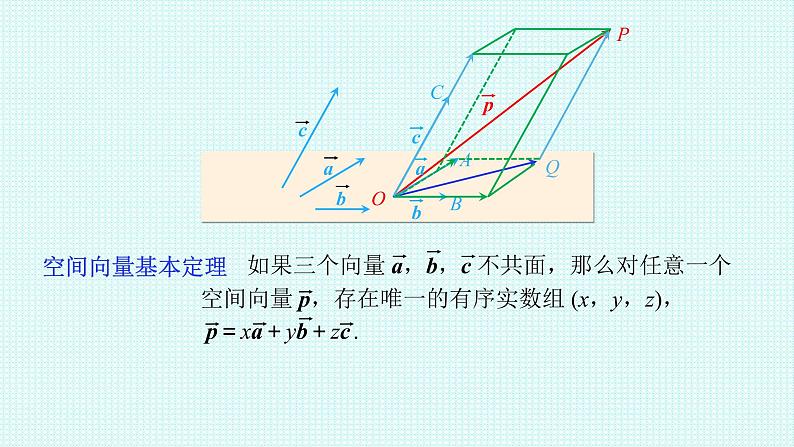
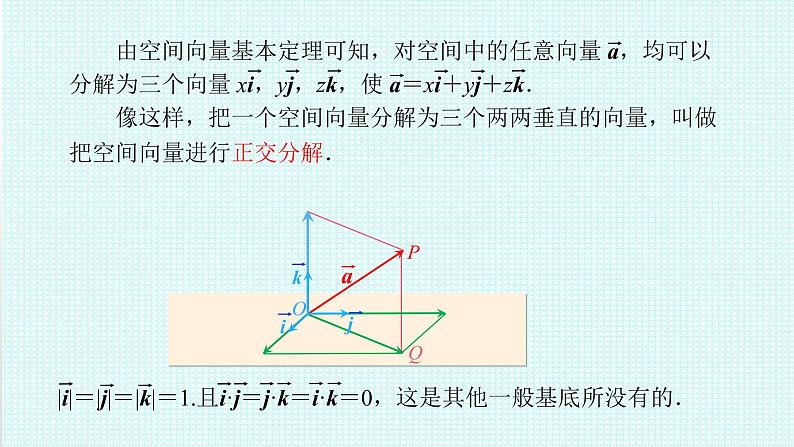
三个向量不共面可以吗
空间的基底有多少个，需要满足什么条件？
答：任意三个不共面的向量都能构成空间的一个基底．空间的基底有无穷多个．
1．判断正误(正确的打“√”，错误的打“×”)(1)只有两两垂直的三个向量才能作为空间向量的一组基底．(　　)(2)若{a，b，c}为空间一个基底，则{－a，b，2c}也可构成空间一个基底．(　　)(3)若三个非零向量a，b，c不能构成空间的一个基底，则a，b，c共面．(　　)
解：因为M为BC的中点．
探究点1　空间向量的基底
由向量共面的充要条件知，存在实数x，y，
空间向量基底的判断依据
(1)判断一组向量能否作为空间向量的一个基底，实质是判断这三个向量是否共面，若不共面，就可以作为空间向量的一个基底．(2)判断基底时，常常依托正方体、长方体、平行六面体、四面体等几何体，用它们从同一顶点出发的三条棱对应的向量为基底，并在此基础上构造其他向量进行相关的判断．　
探究点2　利用基底表示向量
探究点3　空间向量基本定理的应用
例3如图，已知在直三棱柱ABC­A′B′C′中，AC＝BC＝AA′，∠ACB＝90°，D，E分别为AB，BB′的中点．(1)求证：CE⊥A′D；(2)求异面直线CE与AC′所成角的余弦值．