高中数学人教A版 (2019)选择性必修 第一册3.1 椭圆教课ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册3.1 椭圆教课ppt课件，共16页。PPT课件主要包含了椭圆定义，无轨迹，椭圆的标准方程，Pxy，椭圆的两种标准方程，焦点及位置判定，标准方程，abc之间的关系，也可以分情况讨论，角度2定义法等内容，欢迎下载使用。

在日常生活与学习中，可以见到很多有关椭圆的现象，如图所示．
圆是平面内到圆心的距离等于半径的点的集合，
什么是椭圆？椭圆上任意一点的特征是什么？
若将细绳的两端拉开一段距离，分别固定在图板上不同的两点F1、F2处，并用笔尖拉紧绳子，再移动笔尖一周，这时笔尖画出的轨迹是什么图形呢？
1.视笔尖为动点，两个图钉为定点，动点到两定点距离之和符合什么条件，其轨迹是椭圆？
2.改变两图钉之间的距离，使其与绳长相等，画出的图形还是椭圆吗？
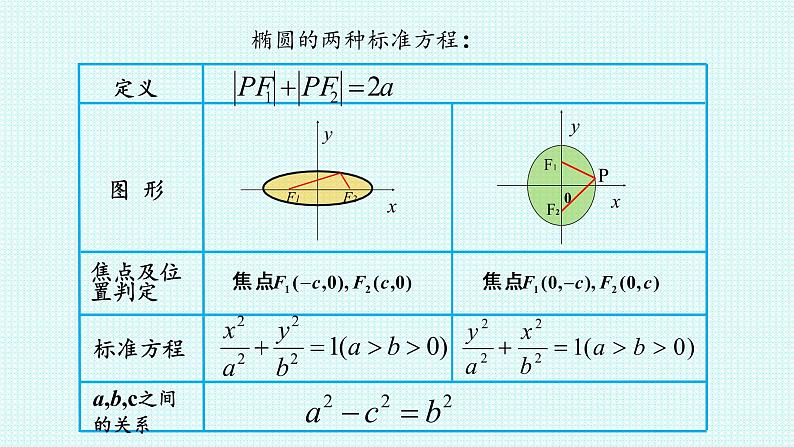
平面内到两个定点F1、F2的距离之和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。
两个定点叫做椭圆的焦点， 两个焦点间的距离叫做椭圆的焦距。
讨论：若把绳长记为2a，两定点间的距离记为2c(c≠0).（1）当2a>2c时，轨迹是 ；（2）当2a=2c时，轨迹 是 ； （3）当2a<2c时， ；
以F1,F2为端点的直线段
|MF1|＋|MF2|＝2a>2c
如图所示：取过焦点F1，F2 的直线为x轴，线段 F1F2 的垂直平分线为y轴，设P(x,y)为椭圆上的任意一点，则椭圆的焦距是2c(c>0)
|MF1|＋|MF2|＝2a
a的长叫做椭圆的半长轴长；b的长叫做椭圆的半短轴长；c叫椭圆的半焦距。
焦点在x轴上椭圆的标准方程
同理可得 焦点在y轴上的椭圆标准方程为：
又c＝4，所以b2＝a2－c2＝25－16＝9．
(2)因为椭圆的焦点在y轴上，所以设标准方程为
又椭圆经过点(0,2)和(1,0)，
(3)设所求椭圆的方程为mx2＋ny2＝1(m＞0，n＞0，m≠n)，依题意有
椭圆方程的求法1．利用待定系数法求椭圆标准方程的一般步骤如下：(1)先确定焦点位置；(2)设出方程；(3)寻求a，b，c的等量关系；(4)求a，b的值，代入所设方程．2．当焦点位置不确定时，可设椭圆方程为mx2＋ny2＝1(m≠n，m＞0，n＞0)．因为焦点位置包括焦点在x轴上(m＜n)或焦点在y轴上(m＞n)两种情况，所以可以避免分类讨论，从而简化运算．
例2.一个动圆与圆Q1：(x＋3)2＋y2＝1外切，与圆Q2：(x－3)2＋y2＝81内切，试求这个动圆圆心的轨迹方程．
两定圆的圆心和半径分别为Q1(－3,0)，r1＝1；Q2(3,0)，r2＝9．
设动圆圆心为M(x，y)，半径为R，由题意有|MQ1|＝1＋R，|MQ2|＝9－R，∴|MQ1|＋|MQ2|＝10＞|Q1Q2|＝6．
由椭圆的定义可知点M在以Q1，Q2为焦点的椭圆上，且a＝5，c＝3，∴b2＝a2－c2＝25－9＝16．
1．若动点轨迹满足椭圆的定义，则根据椭圆的定义来确定a，b，c，从而确定椭圆的标准方程，这种求轨迹方程的方法称为定义法．2．一般步骤：(1)将条件转化为到两定点的距离之和为定值(该定值大于两定点之间的距离)；(2)判断椭圆的中心是否在原点、对称轴是否为坐标轴；(3)确定椭圆的基本量a，b，c，从而确定椭圆的标准方程．
(－9,8)∪(8,25)．
(1)由|PF1|＋|PF2|是定值，求|PF1|·|PF2|的最大值，可考虑用基本不等式；
(2)求焦点三角形的面积，可考虑用定义|PF1|＋|PF2|＝2a及余弦定理先求|PF1|·|PF2|，再考虑用三角形面积公式求面积．
当且仅当|PF1|＝|PF2|＝10时，等号成立，
|PF1|·|PF2|取到最大值100．