2020朔州怀仁一中校云东校区高二下学期期末数学（文科）试题含答案

这是一份2020朔州怀仁一中校云东校区高二下学期期末数学（文科）试题含答案，共9页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。


一、选择题(共12小题,每小题5分,共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)
1.设复数z1，z2在复平面内对应的点关于虚轴对称，且z1＝2＋i，则z2等于( )
A．2＋i B．－2＋i C．2－i D．－2－i
2.函数y＝x|x|的图象大致是( )
A． B． C． D．
3在△ABC中，能使sinA>成立的充分不必要条件是( )
A．A∈ B．A∈ C．A∈ D．A∈
4.已知函数f(x)＝sin(ω>0)的最小正周期为π，则该函数的图象( )
A． 关于点对称 B． 关于直线x＝对称
C． 关于点对称 D． 关于直线x＝对称
5.已知变量x与y负相关，且由观测数据算得样本平均数＝4，＝4.5，则由该观测数据算得的线性回归方程可能是( )
A．＝0.4x＋2.3 B．＝2x－2.4
C．＝－0.3x－3.3 D．＝－2x＋12.5
6.在△ABC中，点D在AB上，CD平分∠ACB.若＝a，＝b，|a|＝1，|b|＝2，则等于( )
A．a＋b B．a＋b C．a＋b D．a＋b
7.设a＝lg37，b＝23.3，c＝0.81.1，则( )
A．b8.设等差数列{an}的前n项和为Sn，若S3＝9，S6＝36，则a7＋a8＋a9等于( )
A． 63 B． 45 C． 36 D． 27
9.已知等比数列{an}中，有a3a11＝4a7，数列{bn}是等差数列，且b7＝a7，则b5＋b9等于（ ）
A． 2 B． 4 C． 8 D． 16
10.已知椭圆C的中心在原点，左焦点F1，右焦点F2均在x轴上，A为椭圆的右顶点，B为椭圆短轴的端点，P是椭圆上一点，且PF1⊥x轴，PF2∥AB，则此椭圆的离心率等于（ ）
A． B． C． D．
11.已知直线ax－by－2＝0与曲线y＝x3在点P(1,1)处的切线互相垂直，则为( )
A． B． － C． D． －
12以椭圆＋＝1的右焦点为圆心，且与双曲线－＝1的渐近线相切的圆的方程是（）
A．x2＋y2－10x＋9＝0 B．x2＋y2－10x－9＝0
C．x2＋y2＋10x＋9＝0 D．x2＋y2＋10x－9＝0
二、填空题(共4小题,每小题5.0分,共20分)
13.命题：“对任意k＞0，方程x2＋x－k＝0有实根”的否定是__________________．
14.若关于实数x的不等式|x－5|＋|x＋3|15.如图，是我国古代数学家赵爽的弦图，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形，如果小正方形的面积为4，大正方形的面积为100，直角三角形中较小的锐角为α，则tanα＝________.

16.A，B，C，D四点在半径为的球面上，且AC＝BD＝5，AD＝BC＝，AB＝CD，则三棱锥D－ABC的体积是________．
三、解答题(共6小题12+12+12+12+12+10=70分)解答写出文字说明,证明过程或演算步骤 17.（本小题满分12分）.在△ABC中，角A，B，C的对边分别为a，b，c，已知向量
m＝(2cs，sin)，n＝(cs，－2sin)，m·n＝－1.
(1)求csA的值；
(2)若a＝2，b＝2，求c的值．
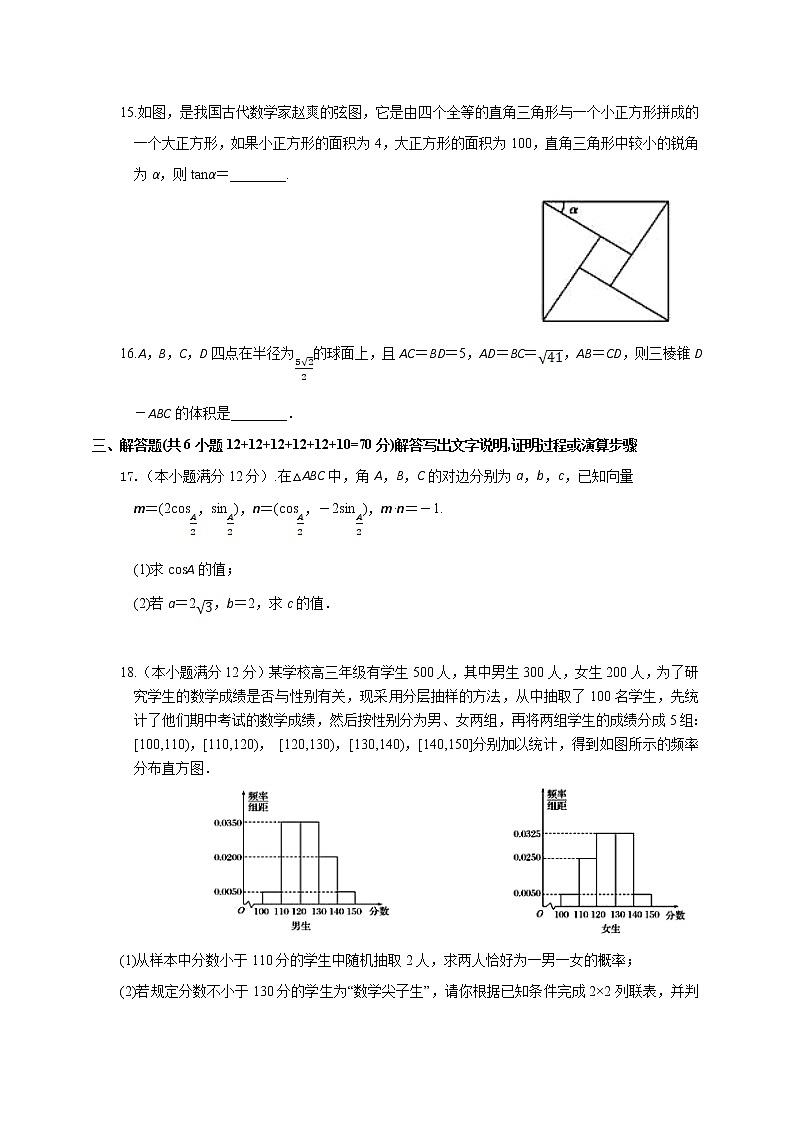
18.（本小题满分12分）某学校高三年级有学生500人，其中男生300人，女生200人，为了研究学生的数学成绩是否与性别有关，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们期中考试的数学成绩，然后按性别分为男、女两组，再将两组学生的成绩分成5组：[100,110)，[110,120)， [120,130)，[130,140)，[140,150]分别加以统计，得到如图所示的频率分布直方图．

(1)从样本中分数小于110分的学生中随机抽取2人，求两人恰好为一男一女的概率；
(2)若规定分数不小于130分的学生为“数学尖子生”，请你根据已知条件完成2×2列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”？

附：K2＝.
19.（本小题满分12分）如图，在三棱柱ABC－A1B1C1中，A1A⊥底面ABC，且△ABC为正三角形，A1A＝AB＝6，D为AC的中点．
(1)求三棱锥C1－BCD的体积；
(2)求证：平面BC1D⊥平面ACC1A1；
(3)求证：直线AB1∥平面BC1D.

20.（本小题满分12分）.已知抛物线C：y2＝2px(p>0)上的一点M(2，y0)到焦点F的距离等于3.
(1)求抛物线C的方程；
(2)若过点D(3,0)的直线l与抛物线C相交于A，B两点，求△ABF面积的最小值．
21.（本小题满分12分）设函数f(x)＝alnx－x，g(x)＝aex－x，其中a为正实数．
(1)若f(x)在(1，＋∞)上是单调递减函数，且g(x)在(2，＋∞)上有最小值，求a的取值围；
(2)若函数f(x)与g(x)都没有零点，求a的取值范围．
22（本小题满分10分）在直角坐标系xOy中，以原点O为极点，以x轴正半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系．设曲线C的参数方程为(θ为参数)，直线l的极坐标方程为ρcs＝2.
(1)写出曲线C的普通方程和直线l的直角坐标方程；
(2)求曲线C上的点到直线l的最大距离．
数学（文）参考答案
1-12 BACAD BCBCD DA
13. 存在k0＞0，方程x2＋x－k0＝0无实根
14. (－∞，8] 15. 16. 20
17.【答案】(1)∵m＝(2cs，sin)，n＝(cs，－2sin)，m·n＝－1，
∴2cs2－2sin2＝－1，∴2csA＝－1，csA＝－.
(2)由(1)知csA＝－，又0＜A＜π， ∴A＝.
∵a＝2，b＝2，由正弦定理得＝， 即＝， ∴sinB＝.
∵0＜B＜π，B＜A，∴B＝，
∴C＝π－A－B＝，∴C＝B，∴c＝b＝2.
【答案】(1)由已知得，抽取的100名学生中，男生60名，女生40名，分数小于等于110分的学生中， 男生人有60×0.05＝3(人)，记为A1，A2，A3；女生有40×0.05＝2(人)，记为B1，B2; 从中随机抽取2名学生，所有的可能结果共有10种，它们是：
(A1，A2)，(A1，A3)，(A2，A3)，(A1，B1)，(A1，B2)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2)，(B1，B2)；
其中，两名学生恰好为一男一女的可能结果共有6种，它们是：
(A1，B1)，(A1，B2)，(A2，B1)，(A2，B2)，(A3，B1)，(A3，B2);
故所求的概率为P＝＝.
(2)由频率分布直方图可知，
在抽取的100名学生中，男生中数学尖子生有60×0.25＝15(人)，女生中数学尖子生有40×0.375＝15(人)． 据此可得2×2列联表如下：

所以得K2＝＝≈1.79.
因为1.79<2.706， 所以没有90%的把握认为“数学尖子生与性别有关”．
(1)解 ∵△ABC为正三角形，D为AC的中点，∴BD⊥AC， 由AB＝6可知CD＝3， BD＝3， ∴S△BCD＝·CD·BD＝. 又∵A1A⊥底面ABC，且A1A＝AB＝6，
∴C1C⊥底面ABC，且C1C＝6， ∴＝·S△BCD·C1C＝9.
(2)证明 ∵A1A⊥底面ABC， ∴A1A⊥BD. 又BD⊥AC， ∴BD⊥平面ACC1A1.
又BD⊂平面BC1D， ∴平面BC1D⊥平面ACC1A1.
证明 连接B1C交BC1于O，连接OD，
在△B1AC中，D为AC的中点，O为B1C的中点，所以OD∥AB1，
又OD⊂平面BC1D， ∴直线AB1∥平面BC1D.
20.解 (1)抛物线的准线方程为x＝－， ∴M(2，y0)到焦点的距离为2＋＝3，
∴p＝2，∴抛物线的方程为y2＝4x.
(2)设AB的方程为x＝my＋3，由得y2－4my－12＝0，设A(x1，y1)，B(x2，y2)， 则y1＋y2＝4m，y1y2＝－12，∴|y1－y2|＝＝，
∴S△ABF＝|FD||y1|＋|FD||y2|＝|y1|＋|y2|＝|y1－y2|＝≥4，
∴当m＝0时，S△ABF取得最小值4.
21.(1)f′(x)＝(x＞0，a＞0)，∵当0＜x＜a时，f′(x)＞0；当x＞a时，f′(x)＜0，
∴f(x)在(0，a)上是增函数，在(a，＋∞)上是减函数，
又f(x)在(1，＋∞)上是减函数， ∴0＜a≤1.
又g′(x)＝aex－1，∴当x＞ln时，g′(x)＞0；x＜时，g′(x)＜0，
∴x＝ln时，g′(x)最小，∴ln＞2，解得a＜ 综上，0＜a＜，即a∈.
(2)由(1)知x＝a时，f(x)取得最大值，当x＝时，g(x)取得最小值，
由题意可得f(a)＜0且g＞0， ∴解得＜a＜e，即a∈.
22.【答案】(1)由ρcs＝2，得ρ(csθ＋sinθ)＝4，
∴直线l的直角坐标方程为x＋y－4＝0. 由得C的普通方程为＋y2＝1.
(2)在曲线C：＋y2＝1上任取一点P(csθ，sinθ)，
则点P到直线l的距离为d＝＝≤3.
∴曲线C上的点到直线l的最大距离为3.