2023年新高考数学一轮复习课时7.2《函数的单调性与导数》达标练习（2份打包，答案版+教师版）

2023年新高考数学一轮复习课时7.2

《函数的单调性与导数》达标练习

一 、选择题

1.若函数f(x)=(x2－2x)ex在(a，b)上单调递减，则b－a的最大值为(　　)

A.2          B.          C.4         D.2

【答案解析】答案为：D

解析：f′(x)=(2x－2)ex＋(x2－2x)ex=(x2－2)ex，令f′(x)<0，

∴－<x<，即函数f(x)的单调递减区间为(－，).

∴b－a的最大值为2.故选D.

2.定义域为R的函数f(x)满足f(1)=1，且f(x)的导函数f′(x)>，则满足2f(x)<x＋1的x的集合为(　　)

A.{x|－1<x<1}      B.{x|x<1}   C.{x|x<－1或x>1}    D.{x|x>1}

【答案解析】答案为：B；

解析：令g(x)=2f(x)－x－1，∵f′(x)>，∴g′(x)=2f′(x)－1>0，

∴g(x)为单调增函数，∵f(1)=1，∴g(1)=2f(1)－1－1=0，

∴当x<1时，g(x)<0，即2f(x)<x＋1，故选B.

3.函数f(x)=ex－ex，x∈R的单调递增区间是(　　)

A.(0，＋∞)      B.(－∞，0)     C.(－∞，1)　　    D.(1，＋∞)

【答案解析】答案为：D

解析：由题意知， f ′(x)=ex－e，令f ′(x)＞0，解得x＞1.故选D.

4.若函数f(x)=kx－ln x在区间(1，＋∞)单调递增，则k的取值范围是(　　)

A.(－∞，－2]        B.(－∞，－1]      C.[2，＋∞)       D.[1，＋∞)

【答案解析】答案为：D

解析：因为f(x)=kx－ln x，所以f′(x)=k－.因为f(x)在区间(1，＋∞)上单调递增，

所以当x＞1时，f′(x)=k－≥0恒成立，即k≥在区间(1，＋∞)上恒 成立.

因为x＞1，所以0＜＜1，所以k≥1.故选D.

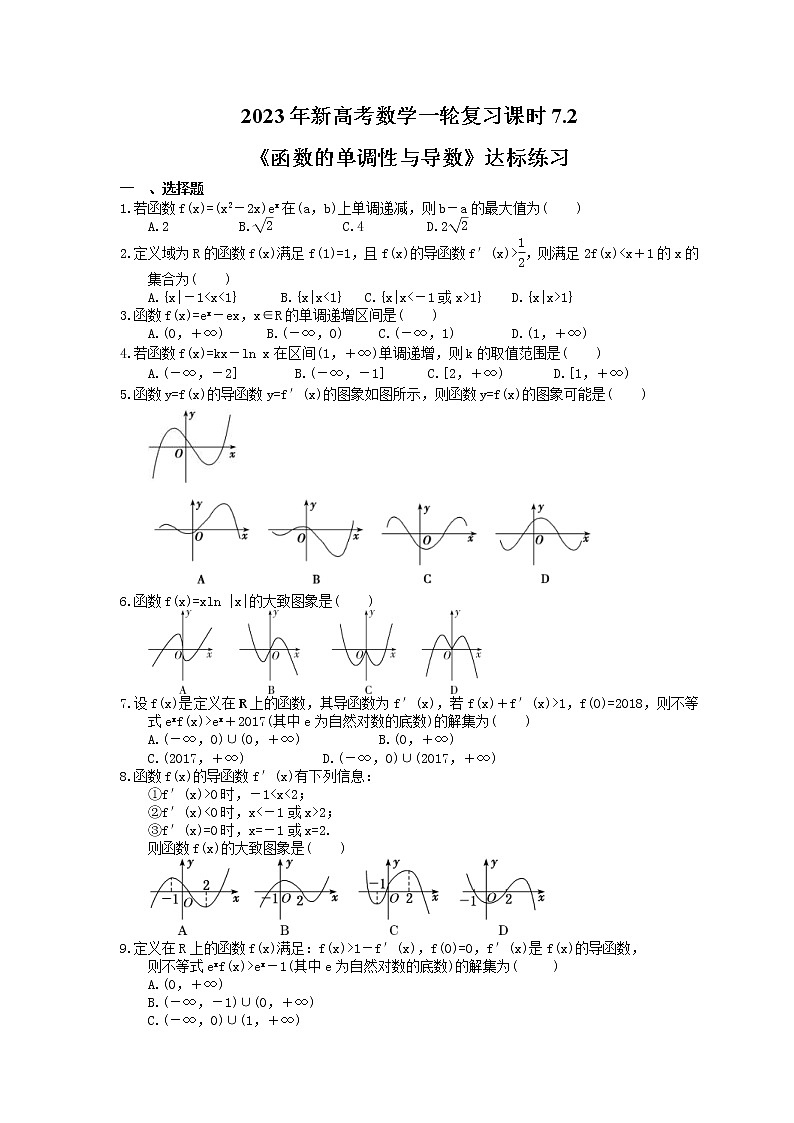
5.函数y=f(x)的导函数y=f′(x)的图象如图所示，则函数y=f(x)的图象可能是(　　)

【答案解析】答案为：D

解析：根据题意，已知导函数的图象有三个零点，且每个零点的两边导函数值的符号相反，因此函数f(x)在这些零点处取得极值，排除A，B；记导函数f′(x)的零点从左到右分别为x1，x2，x3，又在(－∞，x1)上f′(x)＜0，在(x1，x2)上f′(x)＞0，所以函数f(x)在(－∞，x1)上单调递减，排除C，选D.

6.函数f(x)=xln |x|的大致图象是(　　)

【答案解析】答案为：A；

解析：因为函数f(x)=xln |x|，可得f(－x)=－f(x)，f(x)是奇函数，其图象关于原点对称，排除C，D；当x＞0时，f′(x)=ln x＋1，令f′(x)＞0得x＞，得出函数f(x)在(,+∞)上是增函数，排除B，故选A.

7.设f(x)是定义在R上的函数，其导函数为f′(x)，若f(x)＋f′(x)>1，f(0)=2018，则不等式exf(x)>ex＋2017(其中e为自然对数的底数)的解集为(　　)

A.(－∞，0)∪(0，＋∞)           B.(0，＋∞)

C.(2017，＋∞)           D.(－∞，0)∪(2017，＋∞)

【答案解析】答案为：B

解析：设g(x)=exf(x)－ex，则g′(x)=exf(x)＋exf′(x)－ex=ex[f(x)＋f′(x)－1]，

∵f(x)＋f′(x)>1，ex>0，∴g′(x)=ex[f(x)＋f′(x)－1]>0，∴g(x)是R上的增函数.

又g(0)=f(0)－1=2017，∴g(x)>2017的解集为(0，＋∞)，

即不等式exf(x)>ex＋2017的解集为(0，＋∞).故选B.

8.函数f(x)的导函数f′(x)有下列信息：

①f′(x)>0时，－1<x<2；

②f′(x)<0时，x<－1或x>2；

③f′(x)=0时，x=－1或x=2.

则函数f(x)的大致图象是(　　)

【答案解析】答案为：C；

解析：根据信息知，函数f(x)在(－1,2)上是增函数.在(－∞，－1)，

(2，＋∞)上是减函数，故选C.

9.定义在R上的函数f(x)满足：f(x)>1－f′(x)，f(0)=0，f′(x)是f(x)的导函数，

则不等式exf(x)>ex－1(其中e为自然对数的底数)的解集为(　 　)

A.(0，＋∞)

B.(－∞，－1)∪(0，＋∞)

C.(－∞，0)∪(1，＋∞)

D.(－1，＋∞)

【答案解析】答案为：A.

解析：设g(x)=exf(x)－ex，则g′(x)=exf(x)＋exf′(x)－ex.

由已知f(x)>1－f′(x)，可得g′(x)>0在R上恒成立，即g(x)是R上的增函数.

因为f(0)=0，所以g(0)=－1，则不等式exf(x)>ex－1可化为g(x)>g(0)，

所以原不等式的解集为(0，＋∞).

10.已知f(x)=1+x-sin x,则f(2),f(3),f(π)的大小关系正确的是(　 　)

A.f(2)>f(3)>f(π)              B.f(3)>f(2)>f(π)

C.f(2)>f(π)>f(3)              D.f(π)>f(3)>f(2)

【答案解析】答案为：D.

解析:因为f(x)=1+x-sin x,所以f′(x)=1-cos x,

当x∈(0,π]时,f′(x)>0,所以f(x)在(0,π]上是增函数,

所以f(π)>f(3)>f(2).

11.已知函数f(x)=xsin x+cos x+x2,则不等式f(ln x)+f(ln )<2f(1)的解集为(　 　)

A.(e,+∞)                 B.(0,e)      C.(0,)∪(1,e)              D.(,e)

【答案解析】答案为：D.

解析:f(x)=xsin x+cos x+x2是偶函数,

所以f(ln )=f(-ln x)=f(ln x),

所以f(ln x)+f(ln )<2f(1)可变形为f(ln x)<f(1).

f′(x)=xcos x+2x=x(2+cos x),

因为2+cos x>0,所以f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递减,

所以f(ln x)<f(1)等价于-1<ln x<1,所以<x<e.

12.定义在区间(0，＋∞)上的函数y=f(x)使不等式2f(x)＜xf′(x)＜3f(x)恒成立，其中y=f′(x)为y=f(x)的导函数，则(　B　)

A.8＜＜16     B.4＜＜8    C.3＜＜4     D.2＜＜3

【答案解析】答案为：B；

解析：∵xf′(x)－2f(x)＞0，x＞0，

∴′==＞0，

∴y=在(0，＋∞)上单调递增，∴＞，即＞4.

∵xf′(x)－3f(x)＜0，x＞0，

∴′==＜0，

∴y=在(0，＋∞)上单调递减，∴＜，即＜8.

综上，4＜＜8.

二 、填空题

13.若函数f(x)=ax3＋3x2－x恰好有三个单调区间，则实数a的取值范围是　         .

【答案解析】答案为：(－3,0)∪(0，＋∞).

解析：由题意知f′(x)=3ax2＋6x－1，

由函数f(x)恰好有三个单调区间，得f′(x)有两个不相等的零点.

需满足a≠0，且Δ=36＋12a＞0，

解得a＞－3，所以实数a的取值范围是(－3,0)∪(0，＋∞).

14.已知定义域为R的函数f(x)满足f(4)=－3，且对任意的x∈R总有f ′(x)＜3，

则不等式f(x)＜3x－15的解集为________.

【答案解析】答案为：(4，＋∞)

解析：令g(x)=f(x)－3x＋15，则g′(x)=f ′(x)－3＜0，所以g(x)在R上是减函数.

又g(4)=f(4)－3×4＋15=0，所以f(x)＜3x－15的解集为(4，＋∞).

15.已知函数f(x)=－x2＋4x－3ln x在区间[t，t＋1]上不单调，则t的取值范围_______.

【答案解析】答案为：(0，1)∪(2，3)

解析：由题意知f′(x)=－x＋4－=－，

由f′(x)=0，得函数f(x)的两个极值点为1和3，

则只要这两个极值点有一个在区间(t，t＋1)内，

函数f(x)在区间[t，t＋1]上就不单调，

由t<1<t＋1或t<3<t＋1，得0<t<1或2<t<3.

16.设函数f(x)=x3－(1＋a)x2＋4ax＋24a，其中常数a＞1，则f(x)的单调减区间为________.

【答案解析】答案为：(2,2a)

解析：f′(x)=x2－2(1＋a)x＋4a=(x－2)(x－2a)，

由a＞1知，当x＜2时，f′(x)＞0，故f(x)在区间(－∞，2)上单调递增；

当2＜x＜2a时，f′(x)＜0，故f(x)在区间(2,2a)上单调递减；

当x＞2a时，f′(x)＞0，故f(x)在区间(2a，＋∞)上单调递增.

综上，当a＞1时，f(x)在区间(－∞，2)和(2a，＋∞)上单调递增，

在区间(2,2a)上单调递减.