2023年高考数学(文数)一轮复习课时12《实际问题的函数建模》达标练习（2份，答案版+教师版）

2023年高考数学(文数)一轮复习课时12

《实际问题的函数建模》达标练习

一 、选择题

1.下表显示出函数值y随自变量x变化的一组数据，由此判断它最可能的函数模型是(　　)

A.一次函数模型        B.二次函数模型

C.指数函数模型        D.对数函数模型

2.已知正方形ABCD的边长为4，动点P从B点开始沿折线BCDA向A点运动.设点P运动的路程为x，△ABP的面积为S，则函数S=f(x)的图象是(　 　)

3.某企业为节能减排，用9万元购进一台新设备用于生产，第一年需运营费用2万元，从第二年起，每年运营费用均比上一年增加3万元.该设备每年生产的收入均为21万元.设该设备使用了n(n∈N*)年后，盈利总额达到最大值(盈利总额等于总收入减去总成本)，则n等于(　 　)

A.6         B.7        C.8          D.7或8

4.某家具的标价为132元，若降价以九折出售(即优惠10%)，仍可获利10%(相对于进价)，则该家具的进价是(　　)

A.118元         B.105元       C.106元         D.108元

5.某校甲、乙两食堂某年1月营业额相等，甲食堂的营业额逐月增加，并且每月的增加值相同；乙食堂的营业额也逐月增加，且每月增加的百分率相同.已知本年9月份两食堂的营业额又相等，则本年5月份(　　)

A.甲食堂的营业额较高

B.乙食堂的营业额较高

C.甲、乙两食堂的营业额相同

D.不能确定甲、乙哪个食堂的营业额较高

6.我们定义函数y=[x]([x]表示不大于x的最大整数)为“下整函数”；定义y={x}({x}表示不小于x的最小整数)为“上整函数”；

例如[4.3]=4，[5]=5；{4.3}=5，{5}=5.某停车场收费标准为每小时2元，即不超过1小时(包括1小时)收费2元，超过一小时，不超过2小时(包括2小时)收费4元，以此类推.

若李刚停车时间为x小时，则李刚应付费为(单位：元)(　　)

A.2[x＋1]     B.2([x]＋1)     C.2{x}       D.{2x}

7.某品牌电视新品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y(单位：台)与投放市场的月数x之间关系的是(　　)

A.y=100x

B.y=50x2－50x＋100

C.y=50×2x

D.y=100log2x＋100

8.某商店计划投入资金20万元经销甲或乙两种商品.已知经销甲、乙商品所获得的利润分别为P(万元)和Q(万元)，且它们与投入资金x(万元)的关系是：P=，Q= (a>0).若不管资金如何投入，经销这两种商品或其中的一种商品所获得的纯利润总不少于5万元，则a的最小值应为(　　)

A.        B.5         C.        D.2

9.某电视新产品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y 与投放市场的月数x之间关系的是(　　)

A.y＝100x          B.y＝50x2－50x＋100

C.y＝50×2x         D.y＝100log2x＋100

10.已知每生产100克饼干的原材料加工费为1.8元.某食品加工厂对饼干采用两种包装，包装费用、销售价格如下表所示：

则下列说法中正确的是(　 　)

①买小包装实惠；

②买大包装实惠；

③卖3小包比卖1大包盈利多；

④卖1大包比卖3小包盈利多.

A.①③        B.①④         C.②③         D.②④

11.某商场销售A型商品，已知该商品的进价是每件3元，且销售单价与日均销售量的关系如表所示：

请根据以上数据分析，要使该商品的日均销售利润最大，则此商品的定价(单位：元/件)应为(　　)

A.4         B.5.5        C.8.5         D.10

12.已知某服装厂生产某种品牌的衣服，销售量q(x)(单位：百件)关于每件衣服的利润x(单位：元)的函数解析式为 q(x)＝则当该服装厂所获效益最大时，x＝(　　)

A.20         B.60      C.80         D.40

二 、填空题

13.某人计划购买一辆A型轿车，售价为14.4万元，购买后轿车一年的保险费、汽油费、年检费、停车费等约需2.4万元，同时汽车年折旧率约为10%(即这辆车每年减少它的价值的10%)，那么，大约使用________年后，花费在该车上的费用(含折旧费)达到14.4万元.

14.现有含盐7%的食盐水200 g，需将它制成工业生产上需要的含盐5%以上且在6%以下(不含5%和6%)的食盐水，设需要加入4%的食盐水x g，则x的取值范围是________.

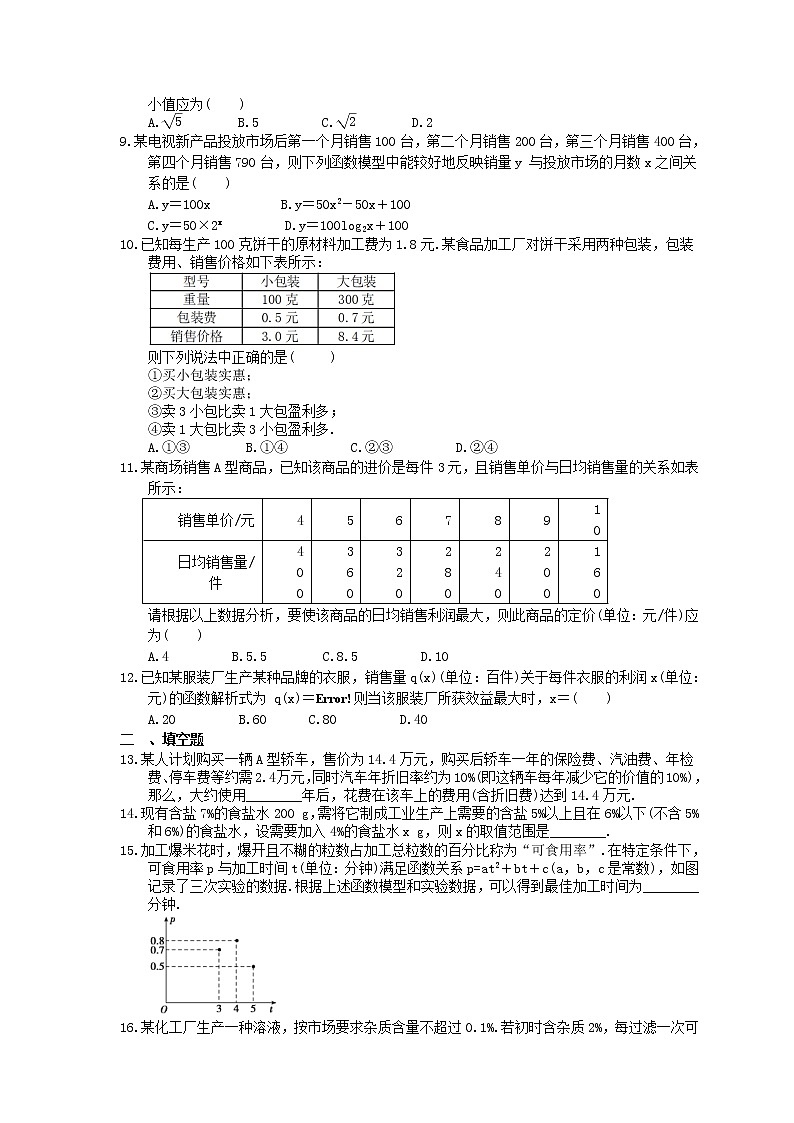
15.加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下，可食用率p与加工时间t(单位：分钟)满足函数关系p=at2＋bt＋c(a，b，c是常数)，如图记录了三次实验的数据.根据上述函数模型和实验数据，可以得到最佳加工时间为________分钟.

16.某化工厂生产一种溶液，按市场要求杂质含量不超过0.1%.若初时含杂质2%，每过滤一次可使杂质含量减少，至少应过滤________次才能达到市场要求.

(已知lg 2≈0.301 0，lg 3≈0.477 1).

0.答案解析

1.答案为：A.

解析：由表中数据知x，y满足关系y=13＋2(x－3).故为一次函数模型.

2.答案为：D；

解析：依题意知当0≤x≤4时，f(x)=2x；当4＜x≤8时，f(x)=8；

当8＜x≤12时，f(x)=24－2x，观察四个选项知D项符合要求.

3.答案为：B；

解析：盈利总额为21n－9－=－n2＋n－9.因为其对应的函数的图象的对称轴方程为n=.所以当n=7时取最大值，即盈利总额达到最大值，故选B.

4.答案为：D；

解析：设家具的进价为a元，由题意知132×(1－10%)－a=10%·a，解得a=108.故选D.

5.答案为：A；

解析：设甲、乙两食堂1月份的营业额均为m，甲食堂的营业额每月增加a(a＞0)，

乙食堂的营业额每月增加的百分率为x，由题意可得，m＋8a=m×(1＋x)8，

则5月份甲食堂的营业额y1=m＋4a，乙食堂的营业额y2=m×(1＋x)4=，

因为y－y=(m＋4a)2－m(m＋8a)=16a2＞0，所以y1＞y2，

故本年5月份甲食堂的营业额较高.

6.答案为：C；

解析：如x=1时，应付费2元，此时2[x＋1]=4,2([x]＋1)=4，排除A、B；当x=0.5时，付费为2元，此时{2x}=1，排除D，故选C.

7.答案为：C；

解析：根据函数模型的增长差异和题目中的数据可知，应为指数型函数模型，代入数据验证即可，故选C.

8.答案为：A

解析：设投入x万元经销甲商品，则经销乙商品投入(20－x)万元，

总利润y=P＋Q=＋·.令y≥5，则＋·≥5对0≤x≤20恒成立.

∴a≥10－，∴a≥对0≤x<20恒成立.

∵f(x)=的最大值为，且x=20时，a≥10－也成立，∴amin=.故选A.

9.答案为：C

解析：根据函数模型的增长差异和题目中的数据可知，应为指数型函数模型，代入数据验证即可得.

10.答案为：D；

解析：买小包装时每克费用为元，买大包装时每克费用为=元，而＞，

所以买大包装实惠，卖3小包的利润为3×(3－1.8－0.5)=2.1(元)，

卖1大包的利润是8.4－1.8×3－0.7=2.3(元)，而2.3＞2.1，

所以卖1大包盈利多，故选D.

11.答案为：C

解析：由题意可设定价为x元/件，利润为y元，则y＝(x－3)[400－40(x－4)]

＝40(－x2＋17x－42)，故当x＝8.5时，y有最大值，故选C.

12.答案为：C

解析：设效益为f(x)，则f(x)＝100xq(x)＝

当0＜x≤20时，f(x)＝＝126 000－，f(x)在区间(0,20]上单调递增，

所以当x＝20时，f(x)有最大值120 000.

当20＜x≤180时，f(x)＝9 000x－300·x，则f′(x)＝9 000－450·，

令f′(x)＝0，∴x＝80.

当20＜x＜80时，f′(x)＞0，f(x)单调递增，

当80≤x≤180时，f′(x)≤0，f(x)单调递减，

所以当x＝80时，f(x)有极大值，也是最大值240 000.故选C.

二 、填空题

13.答案为：4.

解析：设使用x年后花费在该车上的费用达到14.4万元，

依题意可得，14.4(1－0.9x)＋2.4x=14.4.

化简得：x－6×0.9x=0，令f(x)=x－6×0.9x.

因为f(3)=－1.374＜0，f(4)=0.063 4＞0，

所以函数f(x)在(3，4)上应有一个零点.

故大约使用4年后，花费在该车上的费用达到14.4万元.

14.答案为：(100,400)

解析：设y=，令5%＜y＜6%，

即(200＋x)5%＜200×7%＋x·4%＜(200＋x)6%，解得100＜x＜400.

15.答案为：3.75.

解析：由实验数据和函数模型知，二次函数p=at2＋bt＋c的图象过点(3，0.7)，

(4，0.8)，(5，0.5)，分别代入解析式，

得解得

所以p=－0.2t2＋1.5t－2=－0.2(t－3.75)2＋0.812 5，

所以当t=3.75时，可食用率p最大，即最佳加工时间为3.75分钟.

16.答案为：8

解析：设过滤n次才能达到市场要求，则2%(1-)n≤0.1%，即()n≤，

所以nlg≤－1－lg 2，所以n≥7.39，所以n=8.