数学22.3 相似三角形的性质课文配套课件ppt

这是一份数学22.3 相似三角形的性质课文配套课件ppt，共38页。PPT课件主要包含了学习目标，量一量猜一猜，合作探究，是方程思想哦，原来是分类思想呀，都相似，有什么规律吗，相似比，又∠D＝∠A，相信自己是最棒的等内容，欢迎下载使用。

1. 明确相似三角形中对应线段与相似比的关系.（重点）2. 掌握相似三角形的周长比等于相似比及其在实际中的应用.3. 能熟练运用相似三角形的性质解决实际问题．（难点）
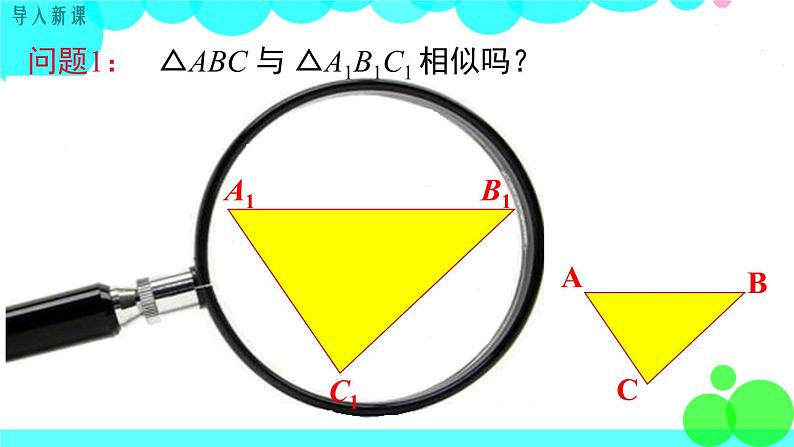
问题1： △ABC 与 △A1B1C1 相似吗？
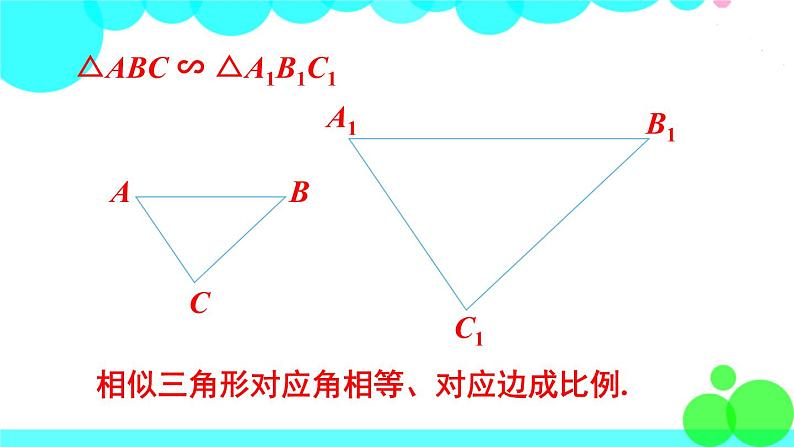
相似三角形对应角相等、对应边成比例.
△ABC ∽ △A1B1C1
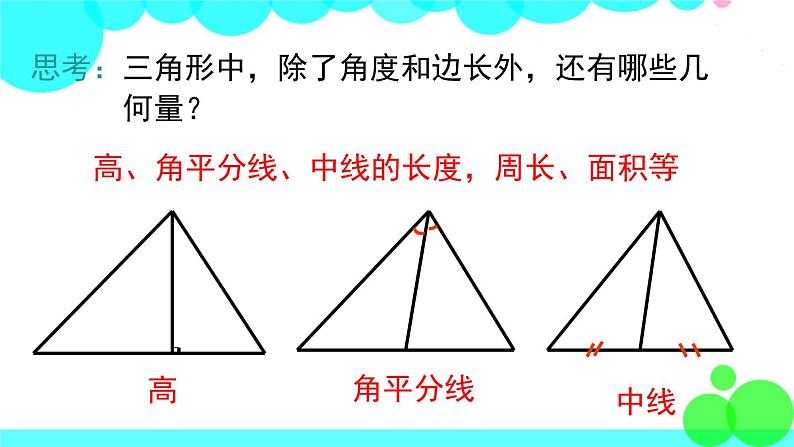
思考：三角形中，除了角度和边长外，还有哪些几 何量？
高、角平分线、中线的长度，周长、面积等
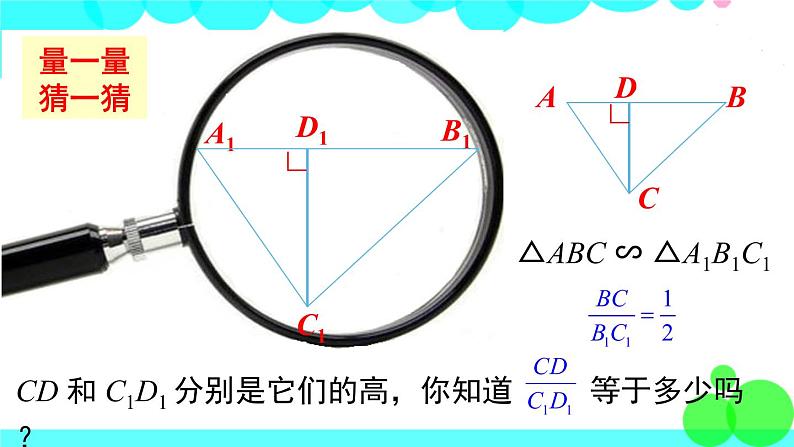
CD 和 C1D1 分别是它们的高，你知道 等于多少吗？
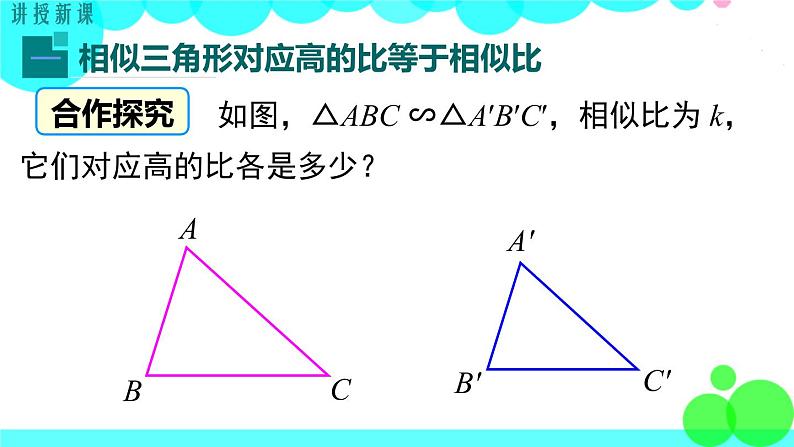
如图，△ABC ∽△A′B′C′，相似比为 k，它们对应高的比各是多少？
∵△ABC ∽△A′B′C′，∴∠B＝∠B' .
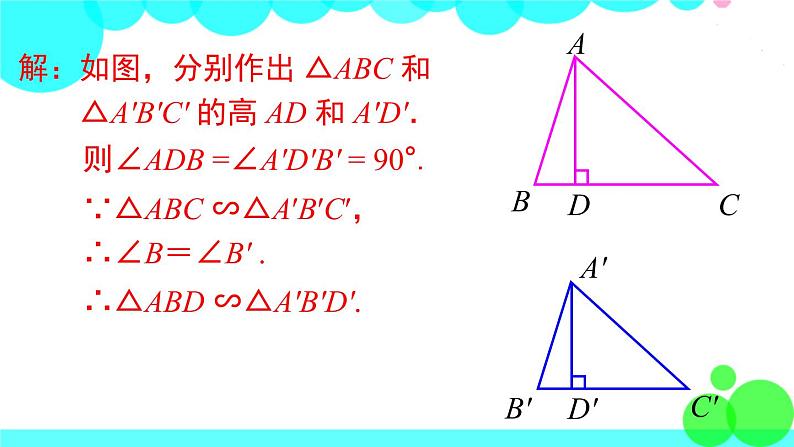
解：如图，分别作出 △ABC 和 △A'B'C' 的高 AD 和 A'D'．
则∠ADB =∠A'D'B' = 90°.
∴△ABD ∽△A'B'D'.
由此得到：相似三角形对应高的比等于相似比．
　　类似的，我们可以得到其余两组对应边上的高的比也等于相似比．
1. △ABC ∽ △A1B1C1 ，BD 和 B1D1 是它们的中线，已知 ，B1D1 = 4 cm，则 BD = cm.
2. △ABC ∽ △A1B1C1，AD 和 A1D1 是 BC 和 B1C1边上的高，已知 AB = 8 cm， A1B1 = 3 cm ，则 △ABC 与 △A1B1C1 的对应高之比为 .
3.如图、电灯 P 在横杆 AB 的正上方，AB 在灯光下的影子为 CD，AB∥CD，AB = 2 m，CD = 4 m，点 P 到 CD 的距离是 3 m，则 P 到 AB 的距离是 m.
例1：如图，AD 是 △ABC 的高，点 P，Q 在 BC 边上，点 R 在 AC 边上，点 S 在 AB 边上，BC = 60 cm，AD = 40 cm，四边形 PQRS 是正方形.
(1) AE 是 △ASR 的高吗？为什么？
(2) △ASR 与 △ABC 相似吗？为什么？
(3) 求正方形 PQRS 的边长.
解： AE 是 △ASR 的高. 理由： ∵AD 是 △ABC 的高， ∴ ∠ADC = 90°.∵四边形 PQRS 是正方形， ∴SR∥BC.∴∠AER =∠ADC = 90°. ∴ AE 是 △ASR 的高.
解： △ASR 与 △ABC 相似. 理由: ∵ SR∥BC， ∴ ∠ASR =∠B，∠ARS =∠C. ∴ △ASR 与 △ABC 相似.
解：∵ △ASR ∽ △ABC，AE、AD分别是 △ASR 和 △ABC 对应边上的高，∴ .设 PQ = x cm，则 SR = DE = x cm，AE = (40 - x) cm .∴ . 解得：x = 24.∴正方形 PQRS 的边长为 24 cm.
BC = 60 cm，AD = 40 cm，四边形 PQRS 是正方形.
变式：如图，AD 是 △ABC 的高，点 P，Q 在 BC 边上，点 R 在 AC 边上，点 S 在 AB 边上，BC = 5 cm，AD = 10 cm，若矩形 PQRS 的长是宽的 2 倍，你能求出这个矩形的面积吗？
如图，AD 是 △ABC 的高，BC = 5 cm，AD = 10 cm.
分析：情况一：SR = 2SP
分析：情况二：SP = 2SR
例2：如图，一块铁皮呈锐角三角形，它的边长 BC = 80 cm，高 AD = 60 cm，要把该铁皮加工成矩形零件，使矩形的两边之比为 2 : 1，且矩形的一边位于边 BC 上，另两个顶点分别在边 AB，AC 上，求这个矩形的边长.
解：如图，矩形 PQRS 为加工后的零件，边 SR 在边 BC 上，顶点 P，Q 分别在边 AB，AC 上，△ABC 的高 AD 交 PQ 于点 E.设 PS = x cm，则 PQ 为 2x cm.
∵PQ∥BC,∴∠APQ =∠ABC,∠AQP =∠ACB,∴△APQ ∽ △ABC.
解方程，得 x = 24，2x = 48.答：这个矩形的零件的边长分别是 48 cm 和 24 cm.
问题：把上图中的高改为中线、角平分线，那么它们对应中线的比，对应角平分线的比等于多少？
图中 △ABC 和 △A′B′C′ 相似，AD、A′D′ 分别为对应边上的中线，BE、B′E′ 分别为对应角的角平分线，那么它们之间有什么关系呢？
已知 △ABC∽△A′B′C′，相似比为k， 求证：
证明：∵ △ABC ∽ △A′B′C′，∴ ∠A′B′C′ =∠ABC， ．又 ∵AD，AD′ 分别为对应边的中线， ∴ △ABD ∽ △A′B′D′.
由此得到： 相似三角形对应的中线的比也等于相似比．
同学们可以试着自己用同样的方法求证三角形对应边上的角平分中线的比等于相似比．
已知：△ABC∽△A′B′C′，相似比为 k，即 求证：
证明：∵△ABC∽△A′B′C′∴ ∠A′B′C′ =∠ABC，∠B′A′C′ =∠BAC．又AD、AD′分别为对应角的平方线， ∴ △ABE∽△A′B′E′.
相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比．
例2：两个相似三角形的两条对应边的长分别是 6cm 和 8 cm，如果它们对应的两条角平分线的和为 42 cm，那么这两条角平分线的长分别是多少？
解：设较短的角平分线长为 x cm，则由相似性质有 .解得 x＝18.较长的角平分线长为 24 cm.故这两条角平分线的长分别为 18 cm，24 cm.
问题：图中 (1)(2)(3) 分别是边长为 1，2，3 的等边三角形，它们都相似吗？
(1)与(2)的相似比=______,(1)与(2)的周长比=______，(1)与(3)的相似比=______,(1)与(3)的周长比=______.
结论： 相似三角形的周长比等于______．
证明：设△ABC ∽ △A1B1C1，相似比为 k，
求证：相似三角形的周长比等于相似比.
想一想：怎么证明这一结论呢？
∴△DEF∽△ABC，相似比为 .∴△DEF的周长 = △ABC 的周长， △DEF 的周长 = 12.
例3.如图，在 △ABC 和 △DEF 中，AB＝2DE，AC＝2DF，∠A＝∠D，△ABC 的周长是 24，求 △DEF 的周长．
解：在 △ABC 和 △DEF 中，
∵ AB＝2DE，AC＝2DF
3. 两个相似三角形对应中线的比为 ，则对应高的比为______ .
2. 相似三角形对应边的比为 2 : 3，那么对应角的角平分线的比为______.
1. 两个相似三角形的相似比为 ，则对应高的比为________， 则对应中线的比为_________.
解：∵ △ABC∽△DEF， 　
解得，EH＝3.2 cm .
答：EH 的长为 3.2 cm.
4.已知 △ABC∽△DEF，BG、EH 分 △ABC 和 △DEF 的角平分线，BC = 6 cm，EF = 4 cm，BG = 4.8 cm.求 EH 的长.
5. 若 △ABC ∽△ A′B′C′ ，它们的周长分别为 60 cm 和 72 cm，且 AB = 15 cm，B′C′ = 24 cm，求 BC，AC，A′B′，A′C′ 的长.
解：∵ △ABC ∽△ A′B′C′ ，它们的周长分别为 60 cm 和 72 cm，∵AB = 15 cm，B′C′ = 24 cm，∴BC = 20 cm， A′B′ = 18 cm， AC = 25 cm，A′C′ = 30 cm.
6.如图，AD 是 △ABC 的高，AD = h，点 R 在 AC 边上，点 S 在 AB 边上，SR⊥AD，垂足为 E.当 时，求 DE 的长.如果 呢？ 　
∴△ASR∽△ABC (两角分别相等的两个三角形相似).
解：∵SR⊥AD，BC⊥AD，
∴SR∥BC.
∴∠ASR =∠B，∠ARS =∠C.
(相似三角形对应高的比等于相似比).
当 时，得 解得：
当 时，得 解得：
选做题：7. 一块直角三角形木板的一条直角边 AB 长为1.5 m，面积为 1.5 m2，要把它加工成一个面积尽可能大的正方形桌面，甲乙两位同学的加工方法如图(1)、(2)所示，请你用学过的知识说明哪位同学的加工方法更好。（加工损耗忽略不计，计算结果中的分数可保留）
8. AD 是 △ABC 的高，BC = 60 cm，AD = 40 cm，求图中小正方形的边长.