山东省菏泽市成武县2022年中考数学一模试题及答案

这是一份山东省菏泽市成武县2022年中考数学一模试题及答案，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
 中考数学一模试题
一、单选题
1．数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线既是轴对称图形，又是中心对称图形的是（　　）
A． B．
C． D．
2．下列各数为负分数的是（　　）
A．－1 B． C．0 D．
3．人体中成熟的红细胞的平均直径为0.000 007 7 m，用科学记数法表示为(　　)
A．7.7×10－5 m B．77×10－6 m
C．77×10－5 m D．7.7×10－6 m
4．如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（　　）

A．（2，5） B．（5，2） C．（2，﹣5） D．（5，﹣2）
5．如图，AB是⊙O的直径，点E、C在⊙O上，点A是弧EC的中点，过点A画⊙O的切线，交BC的延长线于点D，连接EC．若∠ADB=58.5°，则∠ACE的度数为（　　）

A．29.5° B．31.5° C．58.5° D．63°
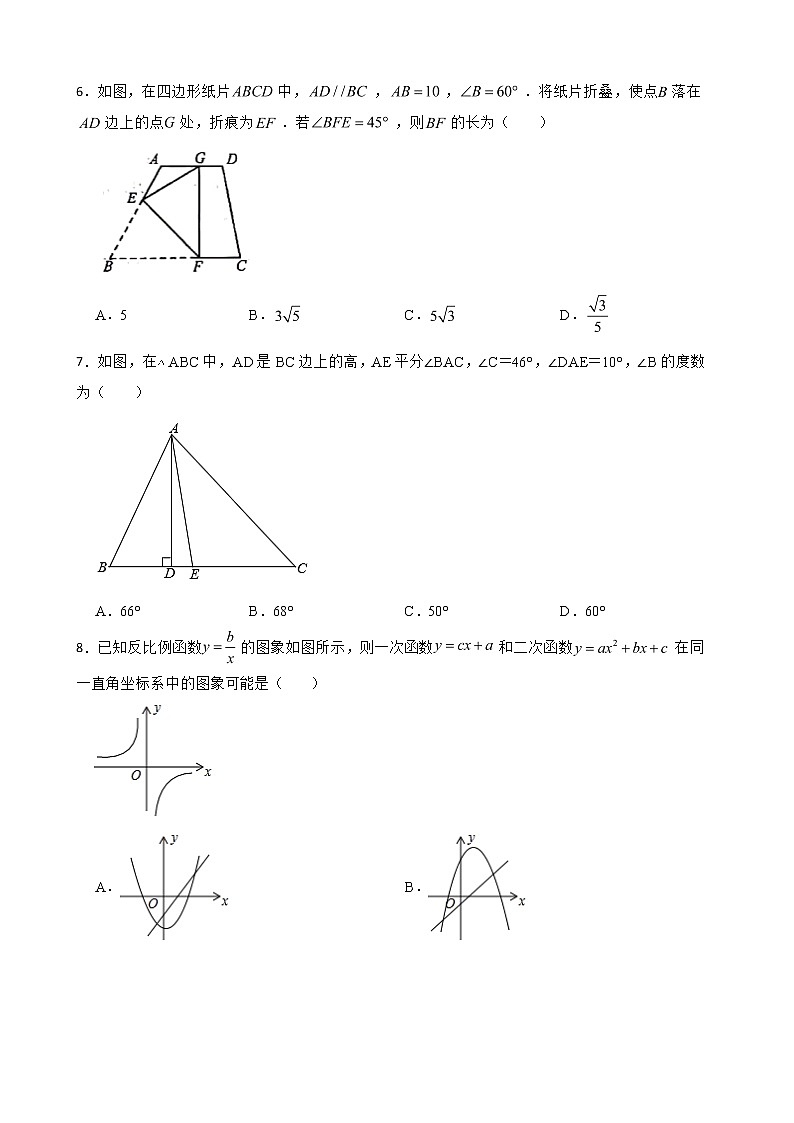
6．如图，在四边形纸片中，，，．将纸片折叠，使点落在边上的点处，折痕为．若，则的长为（　　）

A．5 B． C． D．
7．如图，在ABC中，AD是BC边上的高，AE平分∠BAC，∠C＝46°，∠DAE＝10°，∠B的度数为（　　）

A．66° B．68° C．50° D．60°
8．已知反比例函数的图象如图所示，则一次函数和二次函数在同一直角坐标系中的图象可能是（　　）

A． B．
C． D．
二、填空题
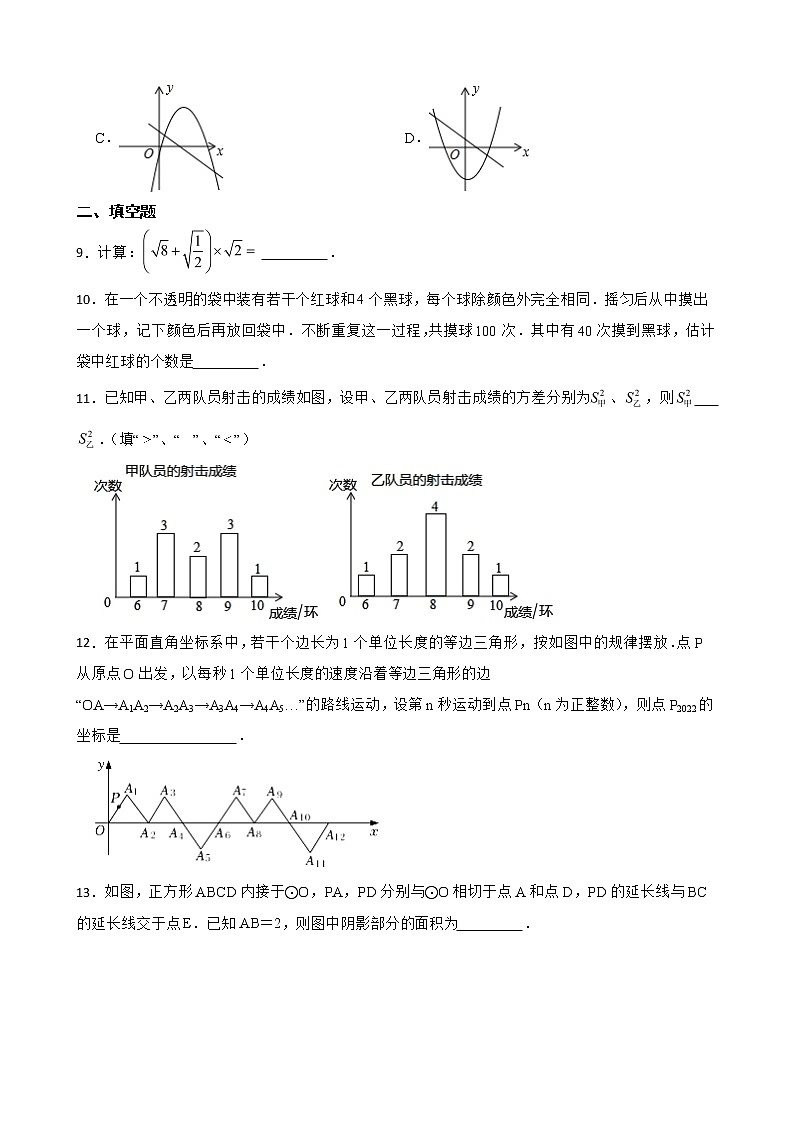
9．计算：　 　．
10．在一个不透明的袋中装有若干个红球和4个黑球，每个球除颜色外完全相同．摇匀后从中摸出一个球，记下颜色后再放回袋中．不断重复这一过程，共摸球100次．其中有40次摸到黑球，估计袋中红球的个数是　 　．
11．已知甲、乙两队员射击的成绩如图，设甲、乙两队员射击成绩的方差分别为、，则　 　．（填“”、“”、“”）

12．在平面直角坐标系中，若干个边长为1个单位长度的等边三角形，按如图中的规律摆放．点P从原点O出发，以每秒1个单位长度的速度沿着等边三角形的边“OA→A1A2→A2A3→A3A4→A4A5…”的路线运动，设第n秒运动到点Pn（n为正整数），则点P2022的坐标是　 　．

13．如图，正方形ABCD内接于⊙O，PA，PD分别与⊙O相切于点A和点D，PD的延长线与BC的延长线交于点E．已知AB＝2，则图中阴影部分的面积为　 　．

14．分解因式：ax4﹣81ay4＝　 　．
三、解答题
15．已知：∠O及其一边上的两点A，B．求作：Rt△ABC，使∠C＝90°，且点C在∠O内部，∠BAC＝∠O．

16．
（1）计算：；
（2）解不等式组：．
17．某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼的高度．如图所示，其中观景平台斜坡的长是20米，坡角为，斜坡底部与大楼底端的距离为74米，与地面垂直的路灯的高度是3米，从楼顶测得路灯项端处的俯角是．试求大楼的高度．
（参考数据：，，，，，）

18．某超市经销甲、乙两种品牌的洗衣液，进货时发现，甲品牌洗衣液每瓶的进价比乙品牌高6元，用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的．销售时，甲品牌洗衣液的售价为36元/瓶，乙品牌洗衣液的售价为28元/瓶．
（1）求两种品牌洗衣液的进价；
（2）若超市需要购进甲、乙两种品牌的洗衣液共120瓶，且购进两种洗衣液的总成本不超过3120元，超市应购进甲、乙两种品牌洗衣液各多少瓶，才能在两种洗衣液完全售出后所获利润最大？最大利润是多少元？
19．如图，在中，E为CD边的中点，连接BE并延长，交AD的延长线于点F，延长ED至点G，使DG＝DE，分别连接AE，AG，FG．

（1）求证：；
（2）当BF平分∠ABC时，四边形AEFG是什么特殊四边形？请说明理由．
20．阅读下面的文字，解答问题，例如：，即，的整数部分是2，小数部分是；
（1）试求：的整数部分．
（2）已知小数部分是n，且，求的x的值．
21．为了解全校学生上学的交通方式，该校九年级（8）班的5名同学联合设计了一份调查问卷，对该校部分学生进行了随机调查．按A（骑自行车）、B（乘公交车）、C（步行）、D（乘私家车）、E（其他方式）设置选项，要求被调查同学从中单选．并将调查结果绘制成条形统计图1和扇形统计图2，根据以上信息，解答下列问题：

（1）本次接受调查的总人数是　 　人，并把条形统计图补充完整　 　；
（2）在扇形统计图中，“步行”的人数所占的百分比是　 　，“其他方式”所在扇形的圆心角度数是　 　；
（3）已知这5名同学中有2名女同学，要从中选两名同学汇报调查结果．请你用列表法或画树状图的方法，求出恰好选出1名男生和1名女生的概率．
22．如图，AB为⊙O的切线，B为切点，过点B作BC⊥OA，垂足为点E，交⊙O于点C，延长CO与AB的延长线交于点D．

（1）求证：AC为⊙O的切线；
（2）若OC＝2，OD＝5，求线段AD和AC的长．
23．如图，抛物线y＝ax2+bx+c与x轴交于A，B两点，与y轴交于点C，已知抛物线的对称轴是直线x＝﹣1，OA＝OC＝2．P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E．

（1）求抛物线的函数表达式；
（2）若点P在第三象限内，且PEOD，求的面积．

答案解析部分
1．【答案】C
【解析】【解答】解：A．是轴对称图形，不是中心对称图形，故此选项不合题意；
B．是轴对称图形，不是中心对称图形，故此选项不合题意；
C．既是中心对称图形，也是轴对称图形，符合题意；
D．是轴对称图形，不是中心对称图形，故此选项不合题意．
故答案为：C．

【分析】根据轴对称图形及中心对称图形的定义逐项判断即可。
2．【答案】B
【解析】【解答】解：A、-1是负整数，故本选项不符合题意；
B、是负分数，故本选项符合题意；
C、0是整数，故本选项不符合题意；
D、 是无理数，故本选项不符合题意；
故答案为：B．
【分析】既是分数又是负数的数，是负分数.
3．【答案】D
【解析】【解答】0.000 007 7m=7.7×10-6m，
故答案为：D．
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
4．【答案】B
【解析】【解答】解：∵线段AB绕点O顺时针旋转90°得到线段A′B′，
∴△ABO≌△A′B′O′，∠AOA′=90°，
∴AO=A′O．
作AC⊥y轴于C，A′C′⊥x轴于C′，
∴∠ACO=∠A′C′O=90°．
∵∠COC′=90°，
∴∠AOA′﹣∠COA′=∠COC′﹣∠COA′，
∴∠AOC=∠A′OC′．
在△ACO和△A′C′O中，
，
∴△ACO≌△A′C′O（AAS），
∴AC=A′C′，CO=C′O．
∵A（﹣2，5），
∴AC=2，CO=5，
∴A′C′=2，OC′=5，
∴A′（5，2）．
故选：B．

【分析】由线段AB绕点O顺时针旋转90°得到线段A′B′可以得出△ABO≌△A′B′O′，∠AOA′=90°，作AC⊥y轴于C，A′C′⊥x轴于C′，就可以得出△ACO≌△A′C′O，就可以得出AC=A′C′，CO=C′O，由A的坐标就可以求出结论．本题考查了旋转的性质的运用，全等三角形的判定及性质的运用，等式的性质的运用，点的坐标的运用，解答时证明三角形全等是关键．
5．【答案】B
【解析】【解答】解：∵AD是⊙O的切线，
∴BA⊥AD，
∵∠ADB=58.5°，
∴∠B=90°-∠ADB=31.5°，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠BAC=90°-∠B=58.5°，
∵点A是弧EC的中点，
∴BA⊥EC，
∴∠ACE=90°-∠BAC=31.5°，
故答案为：B

【分析】先利用三角形的内角和求出∠B=90°-∠ADB=31.5°，再利用点A是弧EC的中点，可得∠ACE=∠B=31.5°。
6．【答案】C
【解析】【解答】解：过点A作 于H，

由折叠知：BF=GF，∠BFE=∠GFE，
，
，
在 中，，，
，
，
，
，
四边形AHFG是矩形，
，
．
故答案为：C．
【分析】过点A作 于H，由折叠知BF=GF，∠BFE=∠GFE=45°，在中，可求出， 再证四边形AHFG是矩形，可得，即得结论.
7．【答案】A
【解析】【解答】解：是边上的高，
，
，
，
，
，
平分，
，
，
故答案为：A．

【分析】先利用三角形的内角和求出，再利用角的运算可求出，再根据角平分线的定义可得，最后利用三角形的内角和求出即可。
8．【答案】D
【解析】【解答】解：∵反比例函数的图象在二、四象限，
∴b＜0，
A、∵二次函数图象开口向上，对称轴在y轴右侧，交y轴的负半轴，
∴a＞0，b＜0，c＜0，
∴一次函数图象应该过第一、二、四象限，A不符合题意；
B、∵二次函数图象开口向下，对称轴在y轴右侧，
∴a＜0，b＞0，
∴与b＜0矛盾，B不符合题意；
C、∵二次函数图象开口向下，对称轴在y轴右侧，
∴a＜0，b＞0，
∴与b＜0矛盾，C不符合题意；
D、∵二次函数图象开口向上，对称轴在y轴右侧，交y轴的负半轴，
∴a＜0，b＜0，c＜0，
∴一次函数图象应该过第一、二、四象限，D符合题意．
故答案为：D．
【分析】由反比例函数的图象在二、四象限可得b＜0，然后逐一分析各选项，根据二次函数图象与系数的关系，先得出a、b、c的符号，由此观察一次函数图象是否与其一致即可.
9．【答案】5
【解析】【解答】解：，
【分析】利用乘法分配律进行二次根式的乘法运算，再计算加法即可.
10．【答案】6
【解析】【解答】解：设袋中红球的个数是x个，根据题意得：
，
解得：x=6，
经检验：x=6是分式方程的解，
即估计袋中红球的个数是6个．
故答案为：6．
【分析】设袋中红球的个数是x个，利用频率估计概率可估计出摸到黑球的概率为，然后根据概率公式构建方程求解即可.
11．【答案】＞
【解析】【解答】解：甲射击的成绩为：6，7，7，7，8，8，9，9，9，10，
乙射击的成绩为：6，7，7，8，8，8，8，9，9，10，
则甲= ×（6+7×3+8×2+9×3+10）=8，
乙=×（6+7×2+8×4+9×2+10）=8，
∴S甲2=×[（6-8）2+3×（7-8）2+2×（8-8）2+3×（9-8）2+（10-8）2]
=×[4+3+3+4]
=1.4；
S乙2=×[（6-8）2+2×（7-8）2+4×（8-8）2+2×（9-8）2+（10-8）2]
=×[4+2+2+4]
=1.2；
∵1.4＞1.2，
∴S甲2＞S乙2，
故答案为：＞．
【分析】根据方差公式分别计算出方差，再比较即可.
12．【答案】（1011，0）
【解析】【解答】解：∵图中是边长为1个单位长度的等边三角形，
过点A1作A1B⊥x轴，
∴OB=BA2=，
∴A1B=，
∴，
A2（1，0），
同理，
A4（2，0），
，
A6（3，0），
，
…
∴An中每6个点的纵坐标规律：，0，，0，﹣，0，
点P从原点O出发，以每秒个单位长度的速度沿着等边三角形的边“…” 的路线运动，1秒钟走一段，
P运动每6秒循环一次，
点P的纵坐标规律：，0，，0，-，0，…，
点P的横坐标规律： ，1，，2，，3，…，，
∵2022＝337×6，
∴点P2022的纵坐标为0，
∴点P2022的横坐标为，
∴点P2022的坐标，
故答案为：（1011，0）．

【分析】先根据前几项的数据与序号的关系可得An中每6个点的纵坐标规律：，0，，0，﹣，0，再求出点P的纵坐标规律：，0，，0，-，0，…，点P的横坐标规律： ，1，，2，，3，…，，结合2022＝337×6，可得点P2022的纵坐标为0，点P2022的横坐标为，从而得解。
13．【答案】
【解析】【解答】解：连接，，

四边形是正方形，
，
是的直径，，
，分别与相切于点和点，
，
四边形是矩形，
，
矩形是正方形，
，，AC//PE，
，
是等腰直角三角形，
，
，，
，
，
图中阴影部分的面积 ，
故答案为：．

【分析】连接AC，OD，利用割补法可得图中阴影部分的面积 。
14．【答案】
【解析】【解答】解：原式＝a（x4﹣81y4）
＝a（x2+9y2）（x2﹣9y2）
＝a（x2+9y2）（x﹣3y）（x+3y），
故答案为：a（x2+9y2）（x﹣3y）（x+3y）．

【分析】先提取公因式a，再利用平方差公式因式分解即可。
15．【答案】解：如图，△ABC即为所求．

【解析】【分析】根据要求作出图象即可。
16．【答案】（1）解：原式


；
（2）解：，
解不等式①得：，
解不等式②得：，
则不等式组的解集为．
【解析】【分析】（1）利用分式的混合运算化简即可；
（2）利用不等式的性质及不等式组的解法求解即可。
17．【答案】解：延长交于点，
过点作，交于点，

由题意得，，
∴四边形为矩形，
∴，.
在中，，
∴，，
∴，，
∴，
∴.
在中，，
∴，
∴，
∴，
∴.
答：大楼的高度约为96米.
【解析】【分析】 延长交于点，过点作，交于点，可证四边形为矩形，可得，.在中，由 ， 求出EM，DM的长.在中由求出BN，根据BC=BN+AE+EM即可得解.
18．【答案】（1）解：设甲品牌洗衣液进价为元/瓶，则乙品牌洗衣液进价为元/瓶，
由题意可得，，
解得，
经检验是原方程的解.
答：甲品牌洗衣液进价为30元/瓶，乙品牌洗衣液进价为24元/瓶.
（2）解：设利润为元，购进甲品牌洗衣液瓶，
则购进乙品牌洗衣液瓶，
由题意可得，，
解得，
由题意可得，，
∵，∴随的增大而增大，
∴当时，取最大值，.
答：购进甲品牌洗衣液40瓶，乙品牌洗衣液80瓶时所获利润最大，最大利润是560元．
【解析】【分析】（1） 设甲品牌洗衣液进价为元/瓶，则乙品牌洗衣液进价为元/瓶，根据“用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的”列出方程并解之即可；
（2）设利润为元，购进甲品牌洗衣液瓶，则购进乙品牌洗衣液瓶，根据“购进两种洗衣液的总成本不超过3120元”列出不等式求出m的范围，再根据总利润=甲的总利润+乙的总利润列出函数关系式，然后利用一次函数的性质求出最大值即可.

19．【答案】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DFE＝∠CBE，
∵E为CD边的中点，
∴DE＝CE，
在△BCE和△FDE中，
，
∴△BCE≌△FDE（AAS）；
（2）解：四边形AEFG是矩形，理由如下：
∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，
∴∠AFB＝∠FBC，
由（1）得：△BCE≌△FDE，
∴BC＝FD，BE＝FE，
∴FD＝AD，
∵GD＝DE，
∴四边形AEFG是平行四边形，
∵BF平分∠ABC，
∴∠FBC＝∠ABF，
∴∠AFB＝∠ABF，
∴AF＝AB，
∵BE＝FE，
∴AE⊥FE，
∴∠AEF＝90°，
∴平行四边形AEFG是矩形．
【解析】【分析】（1）利用“AAS”证明△BCE≌△FDE即可；
（2）先证明四边形AEFG是平行四边形，再结合∠AEF＝90°，可得平行四边形AEFG是矩形。
20．【答案】（1）解：∵，
∴45，
∴13