2021天津市蓟州一中、芦台一中、英华国际学校三校高二下学期期末考试联考数学试题含答案

2020～2021学年度第二学期期末三校联考

高二数学参考答案

第Ⅰ卷（选择题，共45分）

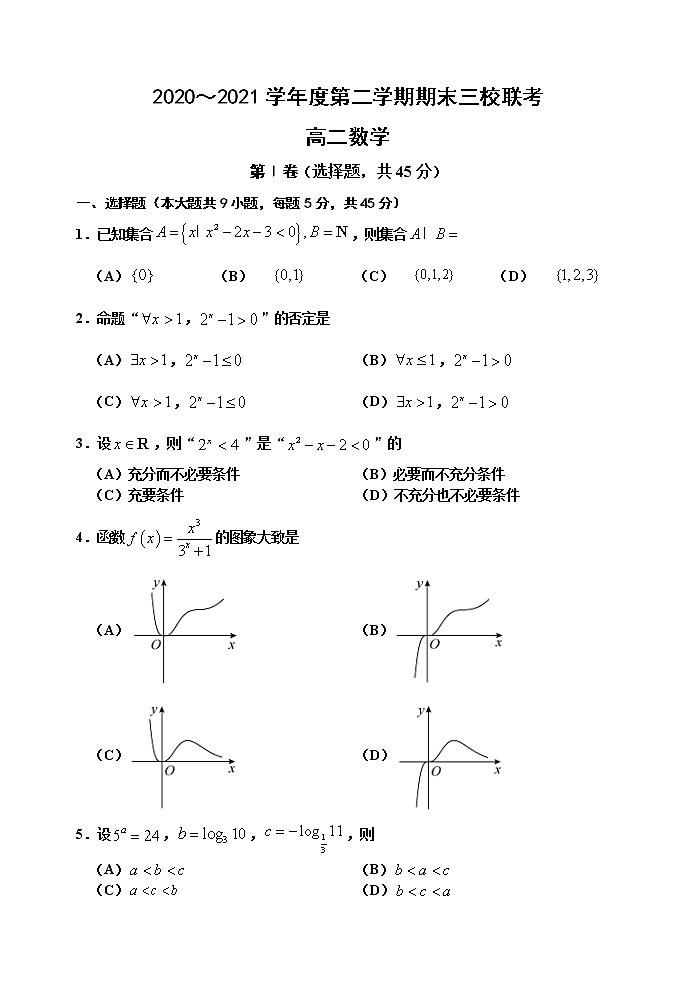
一、选择题（本大题共9小题，每题5分，共45分）

二、填空题（本大题共6小题，每小题5分，共30分）

三、解答题（本大题共5小题，共75分.答题时，请写出必要的推理过程和演算步骤）

16.（本小题满分14分）

【解析】

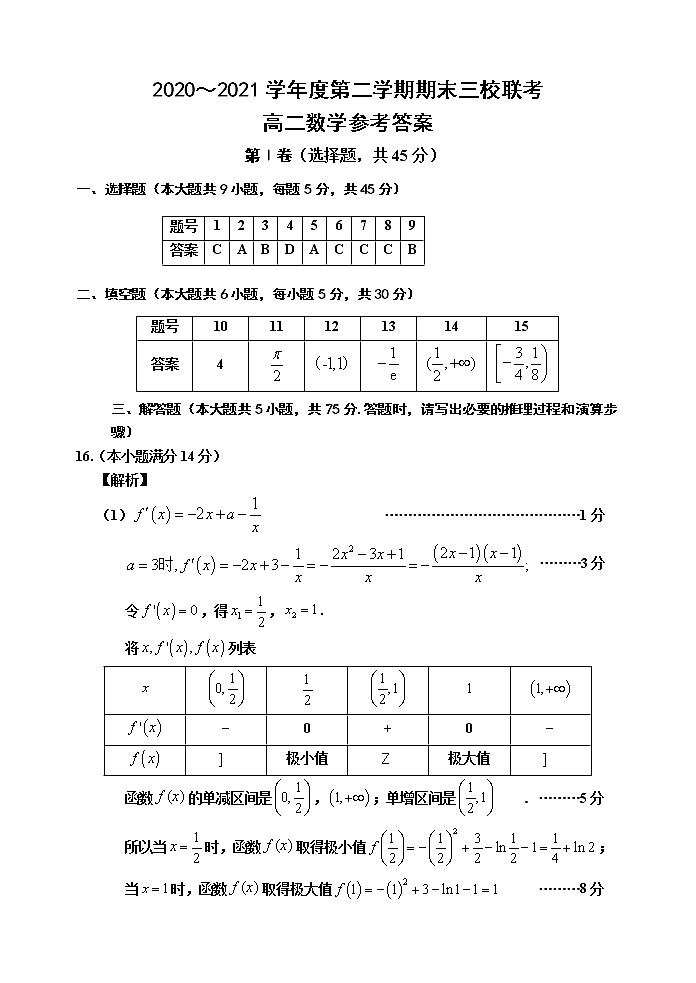
（1）     ……………………………………1分

………3分

令，得，.

将列表

函数的单减区间是，；单增区间是 . ………5分

所以当时，函数取得极小值；

当时，函数取得极大值   ………8分

（2）因为函数在（2，4）上单调递减，则，在x∈（2，4）上恒成立.

  ……………………10分

实数a的取值范围     …………………………………14分

17. （本小题满分15分）

（1）当n=1时，      …………………………1分

当时，……①

①-②得，=2

所以 ，

又因为

所以   ……………………………………………………4分

因为

所以数列{}是公差为1的等差数列，

所以，

所以 ，所以      ……………………7分

（2）     ……………………9分

所以

     =       …………………………………12分

又

所以当n，当n

所以 的最大值为        ……………………………………15分

18．（本小题满分15分）如图，以A为原点建立空间直角坐标系，依题意可得

,,,

,.

又因为M,N分别为和的中点，

得,.

（1）证明：依题意，可得为平面的一个法向量.=.  由此可得 =0，又因为直线平面，所以∥平面                   .                                                                                                                                                                  ………4分

（II）解：，.设为平面的法向量，则

即不妨设，可得.                                                  ……6分

       设为平面DE 法向量，则.扣又，得

不妨设z=1，可得.                  …8分

       因此有              …9分

      所以，平面与平面所成角的余弦值为       …10分

（III）解：依题意，可设，其中，则，从而。又为平面的一个法向量，

由已知，得=，         ………12分

整理得，又因为，解得.

      所以，线段的长为.                      …15分

19.（本小题满分15分）

解：（1）设数列{的公差为d，数列{}的公比为q，

及，得           ………2分

所以                 …………3分

                    …………4分

（Ⅱ）由（1）可得,设的前n项和为

==             ……6分

所以时  ==     …7分

时        …9分

所以           ……10分

（Ⅲ）

……12分

所以

          ……………………………15分

20. 解：（Ⅰ）当时，，.

由，切点，所以切线方程

…4分

（Ⅱ）

（Ⅲ）令，

由，得，    …11分

则，，．

……12分

令，则．               …13分

当时，，为增函数，

所以，即．                                                                                                                           …14分

令，则

当时，，单调递减；

当时，，单调递增．

所以，                     ……15分

故当时，有2个解，即有2个零点，则的取值范围为．                                                                                   ……16分