山西省长治市郊区2022学年七年级（下）数学期末模拟试题

山西省长治市郊区2022学年七年级（下）数学期末模拟试题

一、单项选择（本题包括10个小题，每小题3分，共30分。下列各题，每小题只有一个选项符合题意。）

1. 下列各数中，绝对值最小的数是（　　）

A．π     B．      C．﹣2     D．﹣

2. 若关于x、y的二元一次方程组的解满足x+y<2,则a的取值范围为(    )

A.a<4             B.a>4              C.a<-4              D.a>-4

3. 若不等式组无解，则a的取值范围是(    )

A.a≤-1                  B.a≥-1             C.a<-1                D.a>-1

4. 已知点M(3a-9，1-a)在第三象限，且它的坐标都是整数，则a=(    )

A.1               B.2                C.3              D.4

5. 一个正方体木块的体积是343 cm3,现将它锯成8块同样大小的小正方体木块,则每个小正方体木块的表面积是(　　)

A.cm2       B. cm2     C. cm2       D. cm2

6. 在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位长度得到点Q,则点Q的坐标是(　　)

A.(-2,6)      B.(-2,0)        C.(-5,3)          D.(1,3)

7. 在下列调查中,适宜采用全面调查的是(　　)

A.了解我省中学生的视力情况 

B.了解九(1)班学生校服的尺码情况

C.检测一批电灯泡的使用寿命 

D.调查台州《600全民新闻》栏目的收视率

8. 在平面直角坐标系中，若点A （a，﹣b）在第一象限内，则点B （a，b﹣3）所在的象限是（　　）

A．第一象限    B．第二象限   C．第三象限     D．第四象限

9. 某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5分.娜娜得分要超过90分，设她答对了x道题，则根据题意可列不等式为(    )

A.10x-5(20-x)≥90                     B.10x-5(20-x)＞90

C.10x-(20-x)≥90                      D.10x-(20-x)＞90

10. 甲、乙两人各买了相同数量的信封和信笺,甲每发出一封信只用1张信笺,乙每发出一封信用3张信笺,结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封,则甲、乙两人买的信笺张数、信封个数分别为(　　)

A.150,100                 B.125,75  

C.120,70                 D.100,150

二.填空题(共6题，总计20分)

11. 计算：2﹣2+（﹣1）0＝　　．

12. 不等式5x﹣3＜3x+5的最大整数解是　　．

13. 若点P(x，y)的坐标满足x+y＝xy，则称点P为“和谐点”.请写出一个“和谐点”的坐标为__________.

14. 已知单项式-8a3x+y-zb12cx+y+z与a4b2x-y+3zc6是同类项,则x=__________,y=__________,z=__________. 

15. 一罐饮料净重500克，罐上注有“蛋白质含量≥0.4%”，则这罐饮料中蛋白质的含量至少为__________克.

16. 如图，若AB∥CD，EF与AB、CD分别相交于点E，F，EP与∠EFD的平分线相交于点P，且∠EFD＝60°，EP⊥FP，则∠BEP＝______°．

三.解答题（共7题，总计50分）

17. 计算：2+|3-3|-

18. 解方程组：

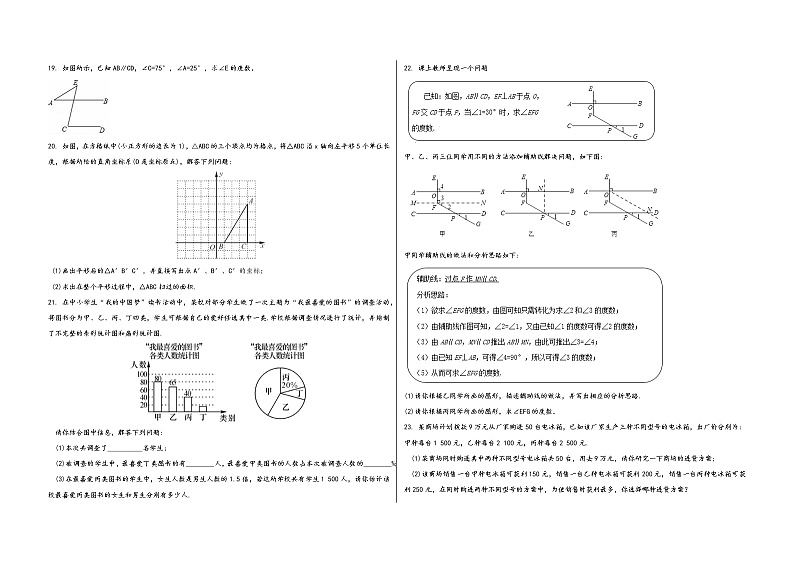
19. 如图所示，已知AB∥CD，∠C=75°，∠A=25°，求∠E的度数．

20. 如图，在方格纸中(小正方形的边长为1)，△ABC的三个顶点均为格点，将△ABC沿x轴向左平移5个单位长度，根据所给的直角坐标系(O是坐标原点)，解答下列问题：

 (1)画出平移后的△A′B′C′，并直接写出点A′、B′、C′的坐标；

 (2)求出在整个平移过程中，△ABC扫过的面积.

21. 在中小学生“我的中国梦”读书活动中，某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动，将图书分为甲、乙、丙、丁四类，学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计，并绘制了不完整的条形统计图和扇形统计图.

  请你结合图中信息，解答下列问题：

  (1)本次共调查了__________名学生；

  (2)被调查的学生中，最喜爱丁类图书的有________人，最喜爱甲类图书的人数占本次被调查人数的________%；

  (3)在最喜爱丙类图书的学生中，女生人数是男生人数的1.5倍，若这所学校共有学生1 500人，请你估计该校最喜爱丙类图书的女生和男生分别有多少人.

22. 课上教师呈现一个问题

甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如下图：

甲同学辅助线的做法和分析思路如下：
 

(1)请你根据乙同学所画的图形，描述辅助线的做法，并写出相应的分析思路.

(2)请你根据丙同学所画的图形，求∠EFG的度数．

23. 某商场计划拨款9万元从厂家购进50台电冰箱，已知该厂家生产三种不同型号的电冰箱，出厂价分别为：甲种每台1 500元，乙种每台2 100元，丙种每台2 500元.

  (1)某商场同时购进其中两种不同型号电冰箱共50台，用去9万元，请你研究一下商场的进货方案；

  (2)该商场销售一台甲种电冰箱可获利150元，销售一台乙种电冰箱可获利200元，销售一台丙种电冰箱可获利250元，在同时购进两种不同型号的方案中，为使销售时获利最多，你选择哪种进货方案？

参考答案

一.选择题

1. D  2. A  3. A  4. B  5. D  6. D  7. B  8. D  9. B  10. A

二. 填空题

11.

12. 3

13. 答案不唯一，如：(2，2)或(0，0)

14. 2 ; 1 ; 3

15. 2

16. 60

三. 解答题

17. 原式=2+3-3-5=3-6.

18. 解：由②，得x=4+y.③

  把③代入①，得3(4+y)+4y=19.解得y=1.

  把y=1代入③，得x=4+1=5.

  ∴原方程组的解为

19. 解：∵AB∥CD，

∴∠BFE=∠C=75°，

∵∠BFE=∠A+∠E，

∴∠E=75°﹣25°=50°．

20. 解：(1)平移后的△A′B′C′如图所示；点A′、B′、C′的坐标分别为(-1，5)、(-4，0)、(-1，0)；

 (2)由平移的性质可知，四边形AA′B′B是平行四边形，

∴△ABC扫过的面积=S四边形AA′B′B+S△ABC=B′B·AC+BC·AC=5×5+×3×5=25+=.

21. 解：(1)40÷20%＝200(人).

(2)200-80-65-40＝15(人)，×100%=40%.

(3)设最喜爱丙类图书的男生人数为x人，则女生人数为1.5x人.根据题意，得

x+1.5x＝1 500×20%.解得x＝120.

当x＝120时，1.5x＝180.

∴最喜爱丙类图书的女生人数为180人，男生人数为120人.

22. （1）解：辅助线：过点P作PN∥EF交AB于点N.
分析思路：

①欲求∠EFG的度数，由辅助线作图可知，∠EFG=∠NPG，
因此，只需转化为求∠NPG的度数；
②欲求∠NPG的度数，由图可知只需转化为求∠1和∠2的度数；
③又已知∠1的度数，所以只需求出∠2的度数；
④由已知EF⊥AB，可得∠4=90°；
⑤由PN∥EF，可推出∠3=∠4；AB∥CD可推出∠2=∠3，由此可推∠2=∠4，
所以可得∠2的度数；
⑥从而可以求出∠EFG的度数.
（2）解：过点O作ON∥FG.
∵ON∥FG.∠1=30°.
∴∠EFG=∠EON ,   ∠1=∠ONC=30°.
∵AB∥CD.
∴∠ONC=∠BON=30°.
∵EF⊥AB.
∴∠EOB=90°.
∴∠EFG=∠EON=∠EOB+∠BON=90°+30°=120°.
 

23. 解：(1)①设购进甲种电冰箱x台，购进乙种电冰箱y台，根据题意，得

解得

故第一种进货方案是购甲、乙两种型号的电冰箱各25台.

②设购进甲种电冰箱x台，购进丙种电冰箱z台，根据题意，得

解得

故第二种进货方案是购进甲种电冰箱35台，丙种电冰箱15台.

③设购进乙种电冰箱y台，购进丙种电冰箱z台，根据题意，得

解得不合题意，舍去.

故此种方案不可行.

  (2)上述的第一种方案可获利：150×25+200×25=8 750(元)，

第二种方案可获利：150×35+250×15=9 000(元)，

因为8 750<9 000，故应选择第二种进货方案，

即购进甲种电冰箱35台，乙种电冰箱15台.