
2022年河北省中考数学模拟自测卷2(word版含答案)
展开2022年河北中考数学模拟自测卷2
一.选择题(共16小题,满分42分)
1.(3分)如图,四点A、B、C、D共线,则图中共有( )条线段.
A.7 B.6 C.5 D.4
2.(3分)下列计算结果一定正确的是( )
A.m2•m3=m6 B.m3+m2=m5
C.﹣(m+1)=﹣m+1 D.(m2+1)0=1
3.(3分)a,b都是实数,且a<b.则下列不等式的变形正确的是( )
A.a+x>b+x B.﹣a+1>﹣b+1 C.3a>3b D.>
4.(3分)设,则可以表示为( )
A. B. C. D.
5.(3分)把(﹣9)﹣(+6)+(﹣1)﹣(﹣2)写成省略括号的和的形式是( )
A.﹣9+6+1﹣2 B.﹣9﹣6﹣1+2 C.﹣9﹣6+1﹣2 D.﹣9﹣6+1+2
6.(3分)如图是一个正方体的表面展开图,则图中“是”这一面的对面的字是( )
A.我 B.爱 C.育 D.才
7.(3分)如图,在▱ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )
A.DE=BF B.AE=CF C.∠ADE=∠CBF D.∠AED=∠CFB
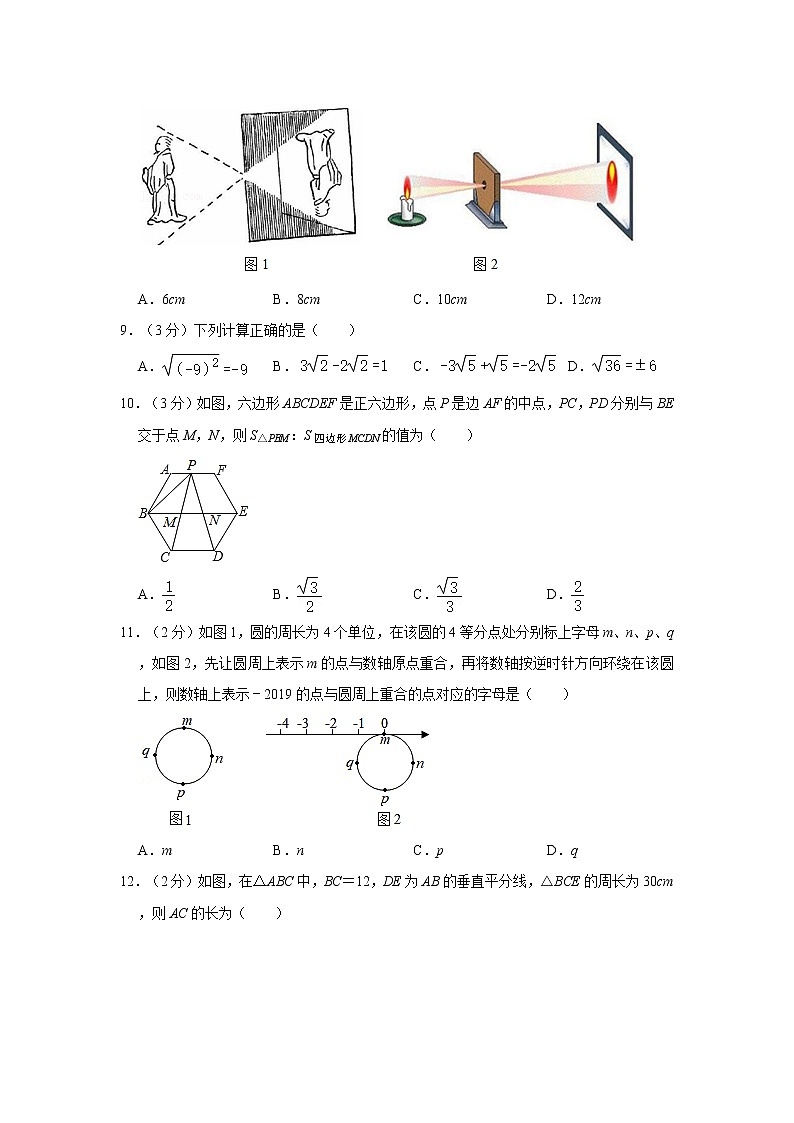
8.(3分)大约在两千四五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是( )
A.6cm B.8cm C.10cm D.12cm
9.(3分)下列计算正确的是( )
A. B. C. D.
10.(3分)如图,六边形ABCDEF是正六边形,点P是边AF的中点,PC,PD分别与BE交于点M,N,则S△PBM:S四边形MCDN的值为( )
A. B. C. D.
11.(2分)如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示﹣2019的点与圆周上重合的点对应的字母是( )
A.m B.n C.p D.q
12.(2分)如图,在△ABC中,BC=12,DE为AB的垂直平分线,△BCE的周长为30cm,则AC的长为( )
A.18 B.12 C.10 D.8
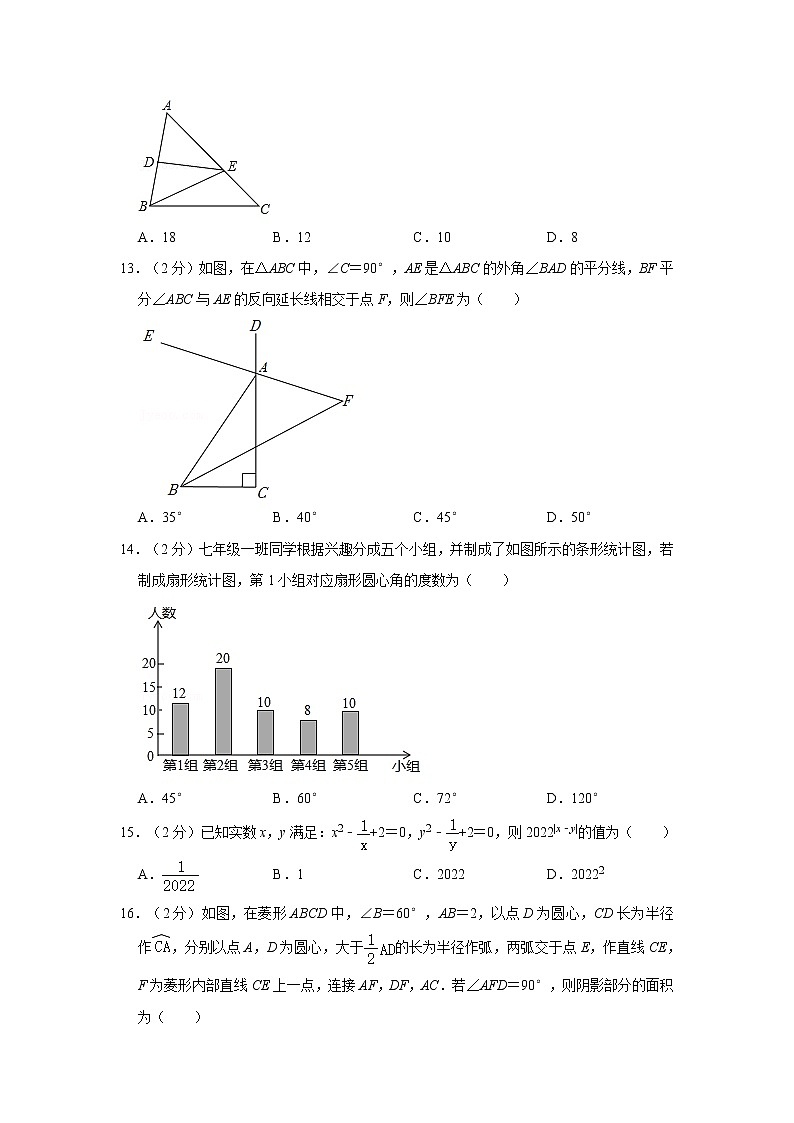
13.(2分)如图,在△ABC中,∠C=90°,AE是△ABC的外角∠BAD的平分线,BF平分∠ABC与AE的反向延长线相交于点F,则∠BFE为( )
A.35° B.40° C.45° D.50°
14.(2分)七年级一班同学根据兴趣分成五个小组,并制成了如图所示的条形统计图,若制成扇形统计图,第1小组对应扇形圆心角的度数为( )
A.45° B.60° C.72° D.120°
15.(2分)已知实数x,y满足:x2﹣+2=0,y2﹣+2=0,则2022|x﹣y|的值为( )
A. B.1 C.2022 D.20222
16.(2分)如图,在菱形ABCD中,∠B=60°,AB=2,以点D为圆心,CD长为半径作,分别以点A,D为圆心,大于的长为半径作弧,两弧交于点E,作直线CE,F为菱形内部直线CE上一点,连接AF,DF,AC.若∠AFD=90°,则阴影部分的面积为( )
A. B. C. D.
二.填空题(共3小题,满分12分,每小题4分)
17.(4分)三种不同类型的地砖的长、宽如图所示,若现有A型地砖4块,B型地砖4块,C型地砖2块,要拼成一个正方形,则应去掉1块地砖;这样的地砖拼法可以得到一个关于m,n的恒等式为 .
18.(4分)如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADB的度数为 度.
19.(4分)如图,直线l与反比例函数y=(k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为 .
三.解答题(共7小题,满分66分)
20.(8分)某房间内每立方米空气中含有3×106个细菌.为了了解某种杀菌剂的效果,科学家们进行了一次测试,发现1毫升杀菌剂可以杀灭2×105个细菌.若要将长10米、宽8米、高3米的房间内的细菌全部杀灭,则需要多少毫升杀菌剂?
21.(9分)已知某公司采购A,B两种不同洗手液共138瓶,设采购了A种洗手液x瓶
(1)嘉嘉说:“买到的B种洗手液的瓶数是A种的三倍.”琪琪由此列出方程:x+3x=138,请用列出的方程判断嘉嘉的说法是否正确;
(2)采购人员说:“B种洗手液比A种至少多32瓶.”请通过列不等式的方法说明A种洗手液最多有几瓶.
22.(9分)将6个球分别放入标有1,2,3,4,5,6这6个号码的盒子中.如图,将一个圆形转盘平均分成3份,分别标上数字1,2,3,现转动转盘两次,两次转得的数字之和是几,从几号盘子中摸出一个球(如:第一次转得数字为2,第二次转得数字为3,则和为5,就从5号盒子中摸球).
(1)求从6号盒子中摸球的概率;
(2)通过计算,判断从几号盒子中摸球的概率最大?
23.(9分)近年来,无人机航拍测量的应用越来越广泛.如图,无人机从A处观测某建筑物至高点O时,俯角为37°;继续水平前行10米到达B处,观测点O,此时的俯角为45°,已知无人机的水平飞行高度为45米.求这栋楼的高度是多少米.(结果精确到0.1)(参考数据:sin37°≈0.60,cos37°≈0.79,tan37°≈0.75,≈1.41)
24.(9分)如图,半径为2的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,求劣弧的长度.
25.(10分)如图,已知抛物线y=ax2+bx+c经过△ABC的三个顶点A(0,1)、B(﹣6,7)、C(﹣4,1).点P是直线AC下方抛物线上的动点.
(1)直接写出抛物线的解析式: ;
(2)过点P作PD⊥AC交AB于点D,连接PC、PA,求四边形PADC的面积的最大值;
(3)如图2,连接PB交AC于点E,当S△BCE=S△AEP时,求点P的坐标.
26.(12分)在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′BC′,其中点A,C的对应点分别为点A′,C′.
(1)如图1,当点A′落在AC的延长线上时,求AA′的长;
(2)如图2,当点C′落在AB的延长线上时,连接CC′,交A′B于点M,求BM的长;
(3)如图3,连接AA′,CC′,直线CC′交AA′于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
2022年河北中考数学模拟自测卷2
参考答案与试题解析
一.选择题(共16小题,满分42分)
1.(3分)如图,四点A、B、C、D共线,则图中共有( )条线段.
A.7 B.6 C.5 D.4
解:图中的线段为AB,AC,AD,BC,BD,CD共6条,
故选:B.
2.(3分)下列计算结果一定正确的是( )
A.m2•m3=m6 B.m3+m2=m5
C.﹣(m+1)=﹣m+1 D.(m2+1)0=1
解:A、m2•m3=m5,故A不符合题意;
B、m3与m2不属于同类项,不能合并,故B不符合题意;
C、﹣(m+1)=﹣m﹣1,故C不符合题意;
D、(m2+1)0=1,故D符合题意;
故选:D.
3.(3分)a,b都是实数,且a<b.则下列不等式的变形正确的是( )
A.a+x>b+x B.﹣a+1>﹣b+1 C.3a>3b D.>
解:A、不等式的两边都加或都减同一个整式,不等号的方向不变,故A错误;
B、不等式的两边都乘或除以同一个负数,不等号的方向改变,故B正确;
C、不等式的两边都乘以或除以同一个正数,不等号的方向不变,故C错误;
D、不等式的两边都乘以或除以同一个正数,不等号的方向不变,故D错误;
故选:B.
4.(3分)设,则可以表示为( )
A. B. C. D.
解:
=
=
=
=
=×4××
=
故选:D.
5.(3分)把(﹣9)﹣(+6)+(﹣1)﹣(﹣2)写成省略括号的和的形式是( )
A.﹣9+6+1﹣2 B.﹣9﹣6﹣1+2 C.﹣9﹣6+1﹣2 D.﹣9﹣6+1+2
解:(﹣9)﹣(+6)+(﹣1)﹣(﹣2)=﹣9﹣6﹣1+2;
故选:B.
6.(3分)如图是一个正方体的表面展开图,则图中“是”这一面的对面的字是( )
A.我 B.爱 C.育 D.才
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“我”与“是”是相对面,
“育”与“人”是相对面,
“们”与“才”是相对面.
故选:A.
7.(3分)如图,在▱ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )
A.DE=BF B.AE=CF C.∠ADE=∠CBF D.∠AED=∠CFB
解:A、由DE=BF,不能推出四边形DEBF是平行四边形,有可能是等腰梯形,故选项A符合题意;
B、∵四边形ABCD是平行四边形,
∴DF∥EB,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴DF∥EB,AB=CD,AD=BC,∠A=∠C,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴DF∥EB,
∴∠CFB=∠ABF,
∵∠AED=∠CFB,
∴∠ABF=∠AED,
∴DE∥BF,
∴四边形DEBF是平行四边形,故选项D不符合题意;
故选:A.
8.(3分)大约在两千四五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是( )
A.6cm B.8cm C.10cm D.12cm
解:设蜡烛火焰的高度是xcm,
由相似三角形对应高的比等于相似比得到:=.
解得x=6.
即蜡烛火焰的高度是6cm.
故选:A.
9.(3分)下列计算正确的是( )
A. B. C. D.
解:A、原式=|﹣9|=9,不符合题意;
B、原式=,不符合题意;
C、原式=﹣2,符合题意;
D、原式=6,不符合题意,
故选:C.
10.(3分)如图,六边形ABCDEF是正六边形,点P是边AF的中点,PC,PD分别与BE交于点M,N,则S△PBM:S四边形MCDN的值为( )
A. B. C. D.
解:设正六边形的边长为a.则S△PCD=2×a2=a2,S四边形BCDE=3×a2=a2,
由题意MN是△PCD的中位线,
∴S△PMN=S△PCD=a2,
∴S四边形MNDC=a2﹣a2=a2,
∴S△BMC=S△DNE=(a2﹣a2)=a2,
∵PM=CM,
∴S△PBM=S△BMC=a2,
∴S△PBM:S四边形MCDN=a2:a2=1:2,
故选:A.
11.(2分)如图1,圆的周长为4个单位,在该圆的4等分点处分别标上字母m、n、p、q,如图2,先让圆周上表示m的点与数轴原点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示﹣2019的点与圆周上重合的点对应的字母是( )
A.m B.n C.p D.q
解:由题意可得,
﹣1与q对应,﹣2与p对应,﹣3与n对应,﹣4与m对应,
2019÷4=504…3,
∴数轴上表示﹣2019的点与圆周上重合的点对应的字母是n,
故选:B.
12.(2分)如图,在△ABC中,BC=12,DE为AB的垂直平分线,△BCE的周长为30cm,则AC的长为( )
A.18 B.12 C.10 D.8
解:∵DE为AB的垂直平分线,
∴AE=BE,
又∵△BCE的周长为30,可得AC+BC=30,
∵BC=12,
∴AC=30﹣12=18,
故选:A.
13.(2分)如图,在△ABC中,∠C=90°,AE是△ABC的外角∠BAD的平分线,BF平分∠ABC与AE的反向延长线相交于点F,则∠BFE为( )
A.35° B.40° C.45° D.50°
解:∵BF平分∠ABC,
∴∠ABF=∠ABC,
∵AE平分∠DAB,
∴∠EAB=∠DAB,
∵∠DAB﹣∠ABC=∠C=90°,
∴∠EAB﹣∠ABF=45°,
∴∠BFE=∠EAB﹣∠ABF=45°,
故选:C.
14.(2分)七年级一班同学根据兴趣分成五个小组,并制成了如图所示的条形统计图,若制成扇形统计图,第1小组对应扇形圆心角的度数为( )
A.45° B.60° C.72° D.120°
解:∵第1组人数占总人数的比例为=,
∴在扇形图中,第1小组对应的圆心角度数是×360°=72°,
故选:C.
15.(2分)已知实数x,y满足:x2﹣+2=0,y2﹣+2=0,则2022|x﹣y|的值为( )
A. B.1 C.2022 D.20222
解:∵x2﹣+2=0,y2﹣+2=0,
∴x2=﹣2,y2=﹣2,
∴x3=1﹣2x,y3=1﹣2y,
∴x3+2x=1,y3+2y=1,
∴x3+2x=y3+2y,
∴x=y,
∴x﹣y=0,
∴2022|x﹣y|
=2022|0|
=20220
=1,
故选:B.
16.(2分)如图,在菱形ABCD中,∠B=60°,AB=2,以点D为圆心,CD长为半径作,分别以点A,D为圆心,大于的长为半径作弧,两弧交于点E,作直线CE,F为菱形内部直线CE上一点,连接AF,DF,AC.若∠AFD=90°,则阴影部分的面积为( )
A. B. C. D.
解:连接AC,CE交AD于H,如图,
在菱形ABCD中,∵∠B=60°,AB=2,
∴∠ADC=60°,DA=DC,
∴△ADC为等边三角形,
∴CA=CD,
由作法得EA=ED,
∴CE垂直平分AD,
∵∠AFD=90°,
∴△ADF为等腰直角三角形,
∴HF=DH=AH=1,
∴DH=AH=1,
∴阴影部分的面积=S扇形ADC﹣S△CDH﹣S△AHF
=﹣×1×﹣×1×1=π﹣.
故选:A.
二.填空题(共3小题,满分12分,每小题4分)
17.(4分)三种不同类型的地砖的长、宽如图所示,若现有A型地砖4块,B型地砖4块,C型地砖2块,要拼成一个正方形,则应去掉1块地砖;这样的地砖拼法可以得到一个关于m,n的恒等式为 (2m+n)2=4m2+4mn+n2 .
解:4块A的面积为:4×m×m=4m2;
4块B的面积为:4×m×n=4mn;
2块C的面积为2×n×n=2n2;
那么这三种类型的砖的总面积应该是:
4m2+4mn+2n2=4m2+4mn+n2+n2=(2m+n)2+n2,
因此,多出了一块C型地砖,去掉一块C型地砖,这两个数的平方为(2m+n)2.
这样的地砖拼法可以得到一个关于m,n的恒等式为:4m2+4mn+n2=(2m+n)2
故答案为:4m2+4mn+n2=(2m+n)2.
18.(4分)如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADB的度数为 85 度.
解:∵∠BAC=40°,∠B=75°,
∴∠C=180°﹣∠BAC﹣∠B
=65°.
∵AD是△ABC的角平分线,
∴∠CAD=20°.
∴∠ADB=∠CAD+∠C
=20°+65°
=85°.
故答案为:85.
19.(4分)如图,直线l与反比例函数y=(k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为 ﹣ .
解:∵AB:BC:CO=1:2:2,
∴设AB=x,BC=CO=2x,
如图1,过D作DE∥l,交OC于E,
∴∠ACD=∠CDE,
∵CD平分∠ACO,
∴∠ACD=∠DCE,
∴∠DCE=∠CDE,
∴DE=CE,
设DE=a,则CE=a,OE=2x﹣a,
∵DE∥AC,
∴△DOE∽△AOC,
∴,即,
∴x(6x﹣5a)=0,
∵x≠0,
∴6x﹣5a=0,a=x,
∵=,
∴=,
∵△COD的面积为6,
∴△AOC的面积为15,
如图2,过B作BG⊥x轴于G,过C作CH⊥x轴于H,
∴BG∥CH,
∴△ABG∽△ACH,
∴,
∵AB:BC=1:2,
∴,
设BG=b,CH=3b,
∵直线l与反比例函数y=(k≠0)的图象在第二象限交于B、C两点,
∴B(,b),C(,3b),
∴GH==﹣,
∵,
∴AG=GH=﹣,
∴OA=AG+OG=﹣=﹣,
∵S△ACO=,
,
k=﹣,
故答案为:﹣.
三.解答题(共7小题,满分66分)
20.(8分)某房间内每立方米空气中含有3×106个细菌.为了了解某种杀菌剂的效果,科学家们进行了一次测试,发现1毫升杀菌剂可以杀灭2×105个细菌.若要将长10米、宽8米、高3米的房间内的细菌全部杀灭,则需要多少毫升杀菌剂?
解:10×8×3×3×106÷(2×105)×1
=7.2×108÷(2×105)
=3.6×103(毫升).
答:需要3.6×103毫升杀菌剂.
21.(9分)已知某公司采购A,B两种不同洗手液共138瓶,设采购了A种洗手液x瓶
(1)嘉嘉说:“买到的B种洗手液的瓶数是A种的三倍.”琪琪由此列出方程:x+3x=138,请用列出的方程判断嘉嘉的说法是否正确;
(2)采购人员说:“B种洗手液比A种至少多32瓶.”请通过列不等式的方法说明A种洗手液最多有几瓶.
解:(1)∵x+3x=138,
∴4x=138,
解得x=34.5,
∵x为是整数,
∴嘉嘉的说法不正确;
(2)设采购了A种洗手液x瓶,则采购了B种洗手液(138﹣x)瓶,
∵B种洗手液比A种至少多32瓶,
∴(138﹣x)﹣x≥32,
解得x≤53,
答:A种洗手液最多有53瓶.
22.(9分)将6个球分别放入标有1,2,3,4,5,6这6个号码的盒子中.如图,将一个圆形转盘平均分成3份,分别标上数字1,2,3,现转动转盘两次,两次转得的数字之和是几,从几号盘子中摸出一个球(如:第一次转得数字为2,第二次转得数字为3,则和为5,就从5号盒子中摸球).
(1)求从6号盒子中摸球的概率;
(2)通过计算,判断从几号盒子中摸球的概率最大?
解:(1)画树状图如下:
共有9种等可能的结果,其中从6号盒子中摸球的结果有1种,
∴从6号盒子中摸球的概率为;
(2)由(1)可知,共有9种等可能的结果,其中从2号盒子中摸球的结果有1种,从3号盒子中摸球的结果有2种,从5号盒子中摸球的结果有2种,从1号盒子中摸球的结果有0种,从4号盒子中摸球的结果有3种,是最多的,
∴从2号盒子中摸球的概率为,从3号盒子中摸球的概率=从5号盒子中摸球的概率=,从1号盒子中摸球的概率为0,从4号盒子中摸球的概率为=,
∵>>>0;
∴从4号盒子中摸球的概率最大.
23.(9分)近年来,无人机航拍测量的应用越来越广泛.如图,无人机从A处观测某建筑物至高点O时,俯角为37°;继续水平前行10米到达B处,观测点O,此时的俯角为45°,已知无人机的水平飞行高度为45米.求这栋楼的高度是多少米.(结果精确到0.1)(参考数据:sin37°≈0.60,cos37°≈0.79,tan37°≈0.75,≈1.41)
解:如图,过点O,作OC⊥AB,交AB的延长线于点C,延长CO交地平面于点E,
由题意可知,∠OAC=37°,∠OBC=45°,AB=10m,AD=45m,
设OC=x米,
在Rt△BOC中,
∵∠OBC=45°,
∴BC=OC=xm,
在Rt△AOC中,AC=AB+BC=(10+x)m,∠OAC=37°,
∴tan37°==≈0.75,
解得x≈30.0,
即OC=30.0米,
∴OE=CE﹣OC=45﹣30.0=15.0(m),
答:这栋楼的高度约是15.0米.
24.(9分)如图,半径为2的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,求劣弧的长度.
解:∵⊙O与正五边形ABCDE的边AB、AE相切于点M、N,
∴OM⊥AB,ON⊥AC,∠A=(5﹣2)×180÷5=108°,
∴∠AMO=∠ANO=90°,
∴∠MON=180°﹣∠A=72°,
∵⊙O的半径为2,
∴劣弧的长度为:=π.
25.(10分)如图,已知抛物线y=ax2+bx+c经过△ABC的三个顶点A(0,1)、B(﹣6,7)、C(﹣4,1).点P是直线AC下方抛物线上的动点.
(1)直接写出抛物线的解析式: y=x2+2x+1 ;
(2)过点P作PD⊥AC交AB于点D,连接PC、PA,求四边形PADC的面积的最大值;
(3)如图2,连接PB交AC于点E,当S△BCE=S△AEP时,求点P的坐标.
解:(1)由题意得,
∴,
∴y=x2+2x+1;
故答案是y=x2+2x+1;
(2)∵A(0,1),B(﹣6,7),
∴直线y=﹣x+1,
设P(m,m2+2m+1),
∴D(m,﹣m+1),
∴PD=(﹣m+1)﹣(m2+2m+1)
=﹣m2﹣3m,
=
=×(﹣m2﹣3m)
=﹣m2﹣6m
=﹣(m+3)2+9,
∴当m=﹣3时,四边形PADC的面积最大值是9;
(3)如图2,
作BG⊥AC于G,作PH⊥AC于H,
∴BG=6,
设E(m,1),
设直线BE的函数关系式是y=kx+b,
∴,
∴,
∴BE的解析式是:y=﹣x+,
由x2+2x+1=﹣x+,
∴x2+x+(1﹣)=0,
∵x=﹣6是方程一个根,
∴由根与系数的关系得,
x1+(﹣6)=﹣,
∴,
把代入y=﹣x+得,
∴y=﹣•+
=,
∴PH=1﹣y=,
∵S△BCE=S△AEP,
∴,
∴6•(m+4)=[﹣m•],
化简得,
m2+7m+12=0,
∴m1=﹣3,m2=﹣4(舍去),
把m=﹣3代入=﹣2,
当x=﹣2时,y==﹣1,
∴P (﹣2,﹣1).
26.(12分)在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′BC′,其中点A,C的对应点分别为点A′,C′.
(1)如图1,当点A′落在AC的延长线上时,求AA′的长;
(2)如图2,当点C′落在AB的延长线上时,连接CC′,交A′B于点M,求BM的长;
(3)如图3,连接AA′,CC′,直线CC′交AA′于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
解:(1)∵∠ACB=90°,AB=5,BC=3,
∴AC==4,
∵∠ACB=90°,△ABC绕点B顺时针旋转得到△A′BC′,点A′落在AC的延长线上,
∴∠A'CB=90°,A'B=AB=5,
Rt△A'BC中,A'C==4,
∴AA'=AC+A'C=8;
(2)过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴∠A'BC=∠ABC,BC'=BC=3,
∵CE∥A'B,
∴∠A'BC'=∠CEB,
∴∠CEB=∠ABC,
∴CE=BC=3,
Rt△ABC中,S△ABC=AC•BC=AB•CD,AC=4,BC=3,AB=5,
∴CD==,
Rt△CED中,DE===,
同理BD=,
∴BE=DE+BD=,C'E=BC'+BE=3+=,
∵CE∥A'B,
∴=,
∴=,
∴BM=;
(3)DE存在最小值1,理由如下:
过A作AP∥A'C'交C'D延长线于P,连接A'C,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴BC=BC',∠ACB=∠A'C'B=90°,AC=A'C',
∴∠BCC'=∠BC'C,
而∠ACP=180°﹣∠ACB﹣∠BCC'=90°﹣∠BCC',
∠A'C'D=∠A'C'B﹣∠BC'C=90°﹣∠BC'C,
∴∠ACP=∠A'C'D,
∵AP∥A'C',
∴∠P=∠A'C'D,
∴∠P=∠ACP,
∴AP=AC,
∴AP=A'C',
在△APD和△A'C'D中,
,
∴△APD≌△A'C'D(AAS),
∴AD=A'D,即D是AA'中点,
∵点E为AC的中点,
∴DE是△AA'C的中位线,
∴DE=A'C,
要使DE最小,只需A'C最小,此时A'、C、B共线,A'C的最小值为A'B﹣BC=AB﹣BC=2,
∴DE最小为A'C=1.
2022年河北省中考数学模拟复习卷一(2份,答案版+原卷版A3版): 这是一份2022年河北省中考数学模拟复习卷一(2份,答案版+原卷版A3版),文件包含2022年河北省中考数学模拟复习卷一含答案A3版doc、2022年河北省中考数学模拟复习卷一原卷版A3版doc等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。
2022年河北省中考数学模拟复习卷四(2份,答案版+原卷版A3版): 这是一份2022年河北省中考数学模拟复习卷四(2份,答案版+原卷版A3版),文件包含2022年河北省中考数学模拟复习卷四含答案A3版doc、2022年河北省中考数学模拟复习卷四原卷版A3版doc等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。
2022年河北省中考数学模拟复习卷二(2份,答案版+原卷版A3版): 这是一份2022年河北省中考数学模拟复习卷二(2份,答案版+原卷版A3版),文件包含2022年河北省中考数学模拟复习卷二含答案A3版doc、2022年河北省中考数学模拟复习卷二原卷版A3版doc等2份试卷配套教学资源,其中试卷共9页, 欢迎下载使用。












