

2022年河北省九年级中考数学模拟自测卷1(word版含答案)
展开2022河北中考数学模拟自测卷1
一.选择题(共16小题,满分42分)
1.(3分)如图,经过直线a外一点O的4条直线中,与直线a相交的直线至少有( )
A.1条 B.2条 C.3条 D.4条
2.(3分)下列计算结果一定正确的是( )
A.m2•m3=m6 B.m3+m2=m5
C.﹣(m+1)=﹣m+1 D.(m2+1)0=1
3.(3分)若m<n,则下列结论不一定成立的是( )
A.m﹣1<n﹣1 B.3m<3n C.﹣>﹣ D.m2<n2
4.(3分)的相反数是( )
A.﹣3 B.3 C. D.﹣9
5.(3分)把(﹣9)﹣(+6)+(﹣1)﹣(﹣2)写成省略括号的和的形式是( )
A.﹣9+6+1﹣2 B.﹣9﹣6﹣1+2 C.﹣9﹣6+1﹣2 D.﹣9﹣6+1+2
6.(3分)有一个正六面体骰子放在桌面上,将骰子如图所示顺时针方向滚动,每滚动90°算一次,则滚动第2020次后,骰子朝下一面的数字是( )
A.5 B.4 C.3 D.2
7.(3分)如图,在▱ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )
A.DE=BF B.AE=CF C.∠ADE=∠CBF D.∠AED=∠CFB
8.(3分)如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
9.(3分)计算:()2=( )
A.﹣4 B.4 C.﹣2 D.2
10.(3分)如图,六边形ABCDEF是正六边形,点P是边AF的中点,PC,PD分别与BE交于点M,N,则S△PBM:S四边形MCDN的值为( )
A. B. C. D.
11.(2分)M为数轴上表示5的点,将点M沿数轴向右移动3个单位长度得到点N,再将点N向左移动7个单位长度得到点P,则点P对应的数是( )
A.﹣4 B.4 C.1 D.9
12.(2分)在Rt△ABC中,∠C=90°,有一点D同时满足以下三个条件:①在直角边BC上;②在∠CAB的角平分线上;③在斜边AB的垂直平分线上,那么∠B为( )
A.15° B.30° C.45° D.60°
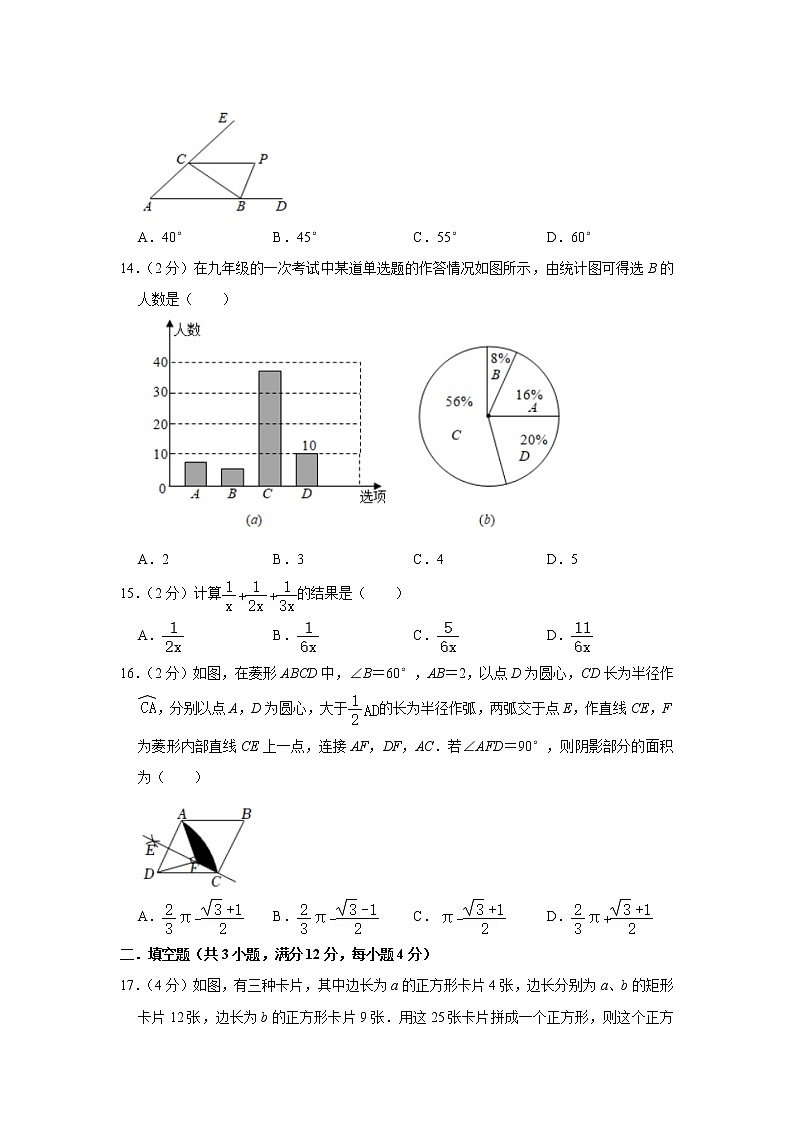
13.(2分)如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC的度数为( )
A.40° B.45° C.55° D.60°
14.(2分)在九年级的一次考试中某道单选题的作答情况如图所示,由统计图可得选B的人数是( )
A.2 B.3 C.4 D.5
15.(2分)计算的结果是( )
A. B. C. D.
16.(2分)如图,在菱形ABCD中,∠B=60°,AB=2,以点D为圆心,CD长为半径作,分别以点A,D为圆心,大于的长为半径作弧,两弧交于点E,作直线CE,F为菱形内部直线CE上一点,连接AF,DF,AC.若∠AFD=90°,则阴影部分的面积为( )
A. B. C. D.
二.填空题(共3小题,满分12分,每小题4分)
17.(4分)如图,有三种卡片,其中边长为a的正方形卡片4张,边长分别为a、b的矩形卡片12张,边长为b的正方形卡片9张.用这25张卡片拼成一个正方形,则这个正方形的边长为 .
18.(4分)如图,△ABC中,点D,E分别在AB,AC边上.比较大小,∠A+∠C ∠1+∠2.
19.(4分)如图,直线l与反比例函数y=(k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为 .
三.解答题(共7小题,满分66分)
20.(8分)太阳是炽热巨大的气体星球,正以每秒约400万吨的速度失去质量.太阳的直径约为140万千米,而地球的半径约为6378千米.请将上述三个数据用科学记数法表示,然后计算一年内太阳要失去多少万吨质量(一年按365天计算).
21.(9分)已知某公司采购A,B两种不同洗手液共138瓶,设采购了A种洗手液x瓶
(1)嘉嘉说:“买到的B种洗手液的瓶数是A种的三倍.”琪琪由此列出方程:x+3x=138,请用列出的方程判断嘉嘉的说法是否正确;
(2)采购人员说:“B种洗手液比A种至少多32瓶.”请通过列不等式的方法说明A种洗手液最多有几瓶.
22.(9分)甲口袋中装有3个相同的小球,它们分别写有数字1,2,3;乙口袋中装有3个相同的小球,它们分别写有数字4,5,6.从两个口袋中各随机取出1个小球.
(Ⅰ)采用树状图法(或列表法)列出所有可能的结果;
(Ⅱ)求取出的两个小球标号都是奇数的概率.
23.(9分)青岛胶东机场即将投入使用,为测量该机场东西两建筑物A、B的距离.如图,勘测无人机在点C处,测得建筑物A的俯角为50°,CA的距离为2千米,然后沿着平行于AB的方向飞行6.4千米到点D,测得建筑物B的俯角为37°,求该机场东西两建筑物AB的距离.(结果精确到0.1千米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
24.(9分)如图,半径为2的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,求劣弧的长度.
25.(10分)已知,直线y=kx﹣1与抛物线y=交于A,B两点(点A在点B的左侧).
(1)当k=时,求A,B两点的坐标;
(2)点P是直线AB下方的抛物线上一点,点Q在y轴上,且四边形APBQ是平行四边形.
①如图1,在(1)的条件下,求▱APBQ的面积;
②当k变化时,Q点是否是y轴上的一个定点?若是,请求出点Q的坐标,若不是,请说明理由.
26.(12分)在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′BC′,其中点A,C的对应点分别为点A′,C′.
(1)如图1,当点A′落在AC的延长线上时,求AA′的长;
(2)如图2,当点C′落在AB的延长线上时,连接CC′,交A′B于点M,求BM的长;
(3)如图3,连接AA′,CC′,直线CC′交AA′于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
2022河北中考数学模拟自测卷1
参考答案与试题解析
一.选择题(共16小题,满分42分)
1.(3分)如图,经过直线a外一点O的4条直线中,与直线a相交的直线至少有( )
A.1条 B.2条 C.3条 D.4条
解:根据经过直线外一点有且只有一条直线和已知直线平行,得出如果有和直线a平行的,只能是一条,
即与直线a相交的直线至少有3条,
故选:C.
2.(3分)下列计算结果一定正确的是( )
A.m2•m3=m6 B.m3+m2=m5
C.﹣(m+1)=﹣m+1 D.(m2+1)0=1
解:A、m2•m3=m5,故A不符合题意;
B、m3与m2不属于同类项,不能合并,故B不符合题意;
C、﹣(m+1)=﹣m﹣1,故C不符合题意;
D、(m2+1)0=1,故D符合题意;
故选:D.
3.(3分)若m<n,则下列结论不一定成立的是( )
A.m﹣1<n﹣1 B.3m<3n C.﹣>﹣ D.m2<n2
解:A.∵m<n,
∴m﹣1<n﹣1,故本选项不符合题意;
B.∵m<n,
∴3m<3n,故本选项不符合题意;
C.∵m<n,
∴﹣>﹣,故本选项不符合题意;
D.当m=﹣2,n=1时,符合m<n,
此时m2>n2,故本选项符合题意;
故选:D.
4.(3分)的相反数是( )
A.﹣3 B.3 C. D.﹣9
解:,
3的相反数是﹣3,
故选:A.
5.(3分)把(﹣9)﹣(+6)+(﹣1)﹣(﹣2)写成省略括号的和的形式是( )
A.﹣9+6+1﹣2 B.﹣9﹣6﹣1+2 C.﹣9﹣6+1﹣2 D.﹣9﹣6+1+2
解:(﹣9)﹣(+6)+(﹣1)﹣(﹣2)=﹣9﹣6﹣1+2;
故选:B.
6.(3分)有一个正六面体骰子放在桌面上,将骰子如图所示顺时针方向滚动,每滚动90°算一次,则滚动第2020次后,骰子朝下一面的数字是( )
A.5 B.4 C.3 D.2
解:观察图形知道点数三和点数四相对,点数二和点数五相对且四次一循环,
∵2020÷4=505,
∴滚动第2020次后与第一个相同,
∴朝下的数字是3的对面4,
故选:B.
7.(3分)如图,在▱ABCD中,点E、F分别在边AB和CD上,下列条件不能判定四边形DEBF一定是平行四边形的是( )
A.DE=BF B.AE=CF C.∠ADE=∠CBF D.∠AED=∠CFB
解:A、由DE=BF,不能推出四边形DEBF是平行四边形,有可能是等腰梯形,故选项A符合题意;
B、∵四边形ABCD是平行四边形,
∴DF∥EB,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴DF∥EB,AB=CD,AD=BC,∠A=∠C,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴DF∥EB,
∴∠CFB=∠ABF,
∵∠AED=∠CFB,
∴∠ABF=∠AED,
∴DE∥BF,
∴四边形DEBF是平行四边形,故选项D不符合题意;
故选:A.
8.(3分)如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
解:由镜面对称可知:△CDE∽△ABE,
∴=,
∴=,
∴AB=15米.
故选:B.
9.(3分)计算:()2=( )
A.﹣4 B.4 C.﹣2 D.2
解:原式=22=4.
故选:B.
10.(3分)如图,六边形ABCDEF是正六边形,点P是边AF的中点,PC,PD分别与BE交于点M,N,则S△PBM:S四边形MCDN的值为( )
A. B. C. D.
解:设正六边形的边长为a.则S△PCD=2×a2=a2,S四边形BCDE=3×a2=a2,
由题意MN是△PCD的中位线,
∴S△PMN=S△PCD=a2,
∴S四边形MNDC=a2﹣a2=a2,
∴S△BMC=S△DNE=(a2﹣a2)=a2,
∵PM=CM,
∴S△PBM=S△BMC=a2,
∴S△PBM:S四边形MCDN=a2:a2=1:2,
故选:A.
11.(2分)M为数轴上表示5的点,将点M沿数轴向右移动3个单位长度得到点N,再将点N向左移动7个单位长度得到点P,则点P对应的数是( )
A.﹣4 B.4 C.1 D.9
解:由数轴上点的平移规律“左减右加”可得,
5+3﹣7=1,
故选:C.
12.(2分)在Rt△ABC中,∠C=90°,有一点D同时满足以下三个条件:①在直角边BC上;②在∠CAB的角平分线上;③在斜边AB的垂直平分线上,那么∠B为( )
A.15° B.30° C.45° D.60°
解:∵D在直角边AB的垂直平分线上,
∴DA=DB,
∴∠DAB=∠B,
∵D在∠CAB的角平分线上,
∴∠DAB=∠DAC,
∴∠CAD=∠DAB=∠B=30°,
故选:B.
13.(2分)如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC的度数为( )
A.40° B.45° C.55° D.60°
解:∵点P是△ABC的外角∠DBC、∠BCE的平分线的交点,
∴∠ECB=2∠PCB,∠DBC=2∠PBC;
∵∠ECB+∠ACB=180°,∠DBC+∠ABC=180°,
∴2∠PCB+2∠PBC+∠ACB+∠ABC=360°,
即2(∠PCB+∠PBC)+∠ACB+∠ABC=360°;
由三角形的内角和定理知:∠PCB+∠PBC=180°﹣∠BPC=180°﹣70°=110°,∠ACB+∠ABC=180°﹣∠BAC,
∴2×110°+180°﹣∠BAC=360°,
解得∠BAC=40°,
故选:A.
14.(2分)在九年级的一次考试中某道单选题的作答情况如图所示,由统计图可得选B的人数是( )
A.2 B.3 C.4 D.5
解:根据题意得:
×8%=4(人),
答:选B的人数是4人;
故选:C.
15.(2分)计算的结果是( )
A. B. C. D.
解:原式=,
故选:D.
16.(2分)如图,在菱形ABCD中,∠B=60°,AB=2,以点D为圆心,CD长为半径作,分别以点A,D为圆心,大于的长为半径作弧,两弧交于点E,作直线CE,F为菱形内部直线CE上一点,连接AF,DF,AC.若∠AFD=90°,则阴影部分的面积为( )
A. B. C. D.
解:连接AC,CE交AD于H,如图,
在菱形ABCD中,∵∠B=60°,AB=2,
∴∠ADC=60°,DA=DC,
∴△ADC为等边三角形,
∴CA=CD,
由作法得EA=ED,
∴CE垂直平分AD,
∵∠AFD=90°,
∴△ADF为等腰直角三角形,
∴HF=DH=AH=1,
∴DH=AH=1,
∴阴影部分的面积=S扇形ADC﹣S△CDH﹣S△AHF
=﹣×1×﹣×1×1=π﹣.
故选:A.
二.填空题(共3小题,满分12分,每小题4分)
17.(4分)如图,有三种卡片,其中边长为a的正方形卡片4张,边长分别为a、b的矩形卡片12张,边长为b的正方形卡片9张.用这25张卡片拼成一个正方形,则这个正方形的边长为 2a+3b .
解:由题可知,25张卡片总面积为4a2+12ab+9b2,
∵4a2+6ab+9b2=(2a+3b)2,
∴这个正方形边长为2a+3b.
故答案为:2a+3b.
18.(4分)如图,△ABC中,点D,E分别在AB,AC边上.比较大小,∠A+∠C = ∠1+∠2.
解:∵∠B+∠A+∠C=180°,∠1+∠2+∠B=180°,
∴∠A+∠C=180°﹣∠B,∠1+∠2=180°﹣∠B,
∴∠A+∠C=∠1+∠2,
故答案为:=.
19.(4分)如图,直线l与反比例函数y=(k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为 ﹣ .
解:∵AB:BC:CO=1:2:2,
∴设AB=x,BC=CO=2x,
如图1,过D作DE∥l,交OC于E,
∴∠ACD=∠CDE,
∵CD平分∠ACO,
∴∠ACD=∠DCE,
∴∠DCE=∠CDE,
∴DE=CE,
设DE=a,则CE=a,OE=2x﹣a,
∵DE∥AC,
∴△DOE∽△AOC,
∴,即,
∴x(6x﹣5a)=0,
∵x≠0,
∴6x﹣5a=0,a=x,
∵=,
∴=,
∵△COD的面积为6,
∴△AOC的面积为15,
如图2,过B作BG⊥x轴于G,过C作CH⊥x轴于H,
∴BG∥CH,
∴△ABG∽△ACH,
∴,
∵AB:BC=1:2,
∴,
设BG=b,CH=3b,
∵直线l与反比例函数y=(k≠0)的图象在第二象限交于B、C两点,
∴B(,b),C(,3b),
∴GH==﹣,
∵,
∴AG=GH=﹣,
∴OA=AG+OG=﹣=﹣,
∵S△ACO=,
,
k=﹣,
故答案为:﹣.
三.解答题(共7小题,满分66分)
20.(8分)太阳是炽热巨大的气体星球,正以每秒约400万吨的速度失去质量.太阳的直径约为140万千米,而地球的半径约为6378千米.请将上述三个数据用科学记数法表示,然后计算一年内太阳要失去多少万吨质量(一年按365天计算).
解:400万=4.00×106,
140万=1.40×106,6378=6.378×103.
一年内太阳失去的质量为400×365×24×3600=1.26144×1010(万吨).
所以一年内太阳要失去约1.26144×1010万吨质量.
21.(9分)已知某公司采购A,B两种不同洗手液共138瓶,设采购了A种洗手液x瓶
(1)嘉嘉说:“买到的B种洗手液的瓶数是A种的三倍.”琪琪由此列出方程:x+3x=138,请用列出的方程判断嘉嘉的说法是否正确;
(2)采购人员说:“B种洗手液比A种至少多32瓶.”请通过列不等式的方法说明A种洗手液最多有几瓶.
解:(1)∵x+3x=138,
∴4x=138,
解得x=34.5,
∵x为是整数,
∴嘉嘉的说法不正确;
(2)设采购了A种洗手液x瓶,则采购了B种洗手液(138﹣x)瓶,
∵B种洗手液比A种至少多32瓶,
∴(138﹣x)﹣x≥32,
解得x≤53,
答:A种洗手液最多有53瓶.
22.(9分)甲口袋中装有3个相同的小球,它们分别写有数字1,2,3;乙口袋中装有3个相同的小球,它们分别写有数字4,5,6.从两个口袋中各随机取出1个小球.
(Ⅰ)采用树状图法(或列表法)列出所有可能的结果;
(Ⅱ)求取出的两个小球标号都是奇数的概率.
解:(Ⅰ)画树状图如下:
所有可能的结果有9种;
(Ⅱ)由(Ⅰ)得:共有9种等可能的结果,取出的两个小球标号都是奇数的结果有2种,
∴取出的两个小球标号都是奇数的概率为.
23.(9分)青岛胶东机场即将投入使用,为测量该机场东西两建筑物A、B的距离.如图,勘测无人机在点C处,测得建筑物A的俯角为50°,CA的距离为2千米,然后沿着平行于AB的方向飞行6.4千米到点D,测得建筑物B的俯角为37°,求该机场东西两建筑物AB的距离.(结果精确到0.1千米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
在Rt△AEC中,∠C=50°,sin∠ECA=,sin50°≈0.77.
∴AE≈0.77×2=1.54(千米),CE=AC•cos50°≈2×0.64=1.28(千米),
∵CD∥AB,
∴∠AED=∠EFB=∠EAB=90°,
∴四边形AEFB是矩形.
∴AE=BF=1.54千米,EF=AB,
在Rt△DFB中,tan∠FDB=,0.75=,
解得:DF≈2.1(千米),
∴EF=CD+DF﹣CE=6.4+2.1﹣1.28≈7.2(千米),
∴AB=EF=7.2(千米),
答:该机场东西两建筑物AB的距离约为7.2千米.
24.(9分)如图,半径为2的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,求劣弧的长度.
解:∵⊙O与正五边形ABCDE的边AB、AE相切于点M、N,
∴OM⊥AB,ON⊥AC,∠A=(5﹣2)×180÷5=108°,
∴∠AMO=∠ANO=90°,
∴∠MON=180°﹣∠A=72°,
∵⊙O的半径为2,
∴劣弧的长度为:=π.
25.(10分)已知,直线y=kx﹣1与抛物线y=交于A,B两点(点A在点B的左侧).
(1)当k=时,求A,B两点的坐标;
(2)点P是直线AB下方的抛物线上一点,点Q在y轴上,且四边形APBQ是平行四边形.
①如图1,在(1)的条件下,求▱APBQ的面积;
②当k变化时,Q点是否是y轴上的一个定点?若是,请求出点Q的坐标,若不是,请说明理由.
(1)当k=时,直线的解析式为y=x﹣1,
∵直线y=x﹣1与抛物线y=交于A,B两点,
∴,
解得:,,
∵点A在点B的左侧,
∴A(﹣,﹣),B(2,);
(2)①∵点Q在y轴上,
∴设Q(0,m),
∵四边形APBQ是平行四边形,点Q(0,m)向左平移个单位,再向下平移m﹣(﹣)=(m+)个单位得到A(﹣,﹣),
∴点B(2,)向左平移个单位,再向下平移m﹣(﹣)=(m+)个单位得到P(2﹣,﹣m﹣),即P(,﹣m﹣),
把P(,﹣m﹣)代入y=得:﹣m﹣=×﹣,
解得:m=﹣,
∴Q(0,﹣),P(,﹣),
如图1,过点A作AC⊥y轴于点C,过点B作BD⊥AC于点D,过点P作PE⊥AD于点E,则C(0,),E(,﹣),D(2,﹣),
∴S▱ABPQ=S△ACQ+S梯形CQBD﹣S△APE﹣S梯形EPBD
=•AC•CQ+(CQ+BD)•CD﹣•AE•PE﹣•(PE+BD)•DE
=××+×(+)×2﹣×2×1﹣×(1+)×
=;
②点Q是y轴上的一个定点,
把y=kx﹣1代入y=得:kx﹣1=,
整理得:x2﹣2kx﹣1=0,
设关于x的方程x2﹣2kx﹣1=0的两个实数根为x1、x2(x1<0<x2),则x1+x2=2k,x1x2=﹣1,
设A(x1,y1),B(x2,y2),Q(0,m),则y1=x12﹣,y2=x22﹣,
当k>0时,如图2,
∵四边形APBQ是平行四边形,点Q(0,m)向左平移﹣x1个单位,再向下平移(m﹣y1)个单位得到A(x1,y1),
∴点B(x2,y2)向左平移﹣x1个单位,再向下平移(m﹣y1)个单位得到P(x1+x2,y2﹣m+y1),
把P(x1+x2,y2﹣m+y1)代入y=得:y2﹣m+y1=(x1+x2)2﹣,
∴x22﹣﹣m+x12﹣=(x1+x2)2﹣,
∴﹣﹣m=x1x2,
∴﹣﹣m=﹣1,
∴m=﹣,
∴Q(0,﹣);
当k<0时,如图3,
∵四边形APBQ是平行四边形,点Q(0,m)向左平移x2个单位,再向下平移(m﹣y2)个单位得到B(x2,y2),
∴点A(x1,y1)向左平移x2个单位,再向下平移(m﹣y2)个单位得到P(x1+x2,y1﹣m+y2),
把P(x1+x2,y1﹣m+y2)代入y=得:y1﹣m+y2=(x1+x2)2﹣,
∴x12﹣﹣m+x22﹣=(x1+x2)2﹣,
∴﹣﹣m=x1x2,
∴﹣﹣m=﹣1,
∴m=﹣,
∴Q(0,﹣),
综上所述,点Q是y轴上的一个定点,Q(0,﹣).
26.(12分)在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′BC′,其中点A,C的对应点分别为点A′,C′.
(1)如图1,当点A′落在AC的延长线上时,求AA′的长;
(2)如图2,当点C′落在AB的延长线上时,连接CC′,交A′B于点M,求BM的长;
(3)如图3,连接AA′,CC′,直线CC′交AA′于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值?若存在,求出DE的最小值;若不存在,请说明理由.
解:(1)∵∠ACB=90°,AB=5,BC=3,
∴AC==4,
∵∠ACB=90°,△ABC绕点B顺时针旋转得到△A′BC′,点A′落在AC的延长线上,
∴∠A'CB=90°,A'B=AB=5,
Rt△A'BC中,A'C==4,
∴AA'=AC+A'C=8;
(2)过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴∠A'BC=∠ABC,BC'=BC=3,
∵CE∥A'B,
∴∠A'BC'=∠CEB,
∴∠CEB=∠ABC,
∴CE=BC=3,
Rt△ABC中,S△ABC=AC•BC=AB•CD,AC=4,BC=3,AB=5,
∴CD==,
Rt△CED中,DE===,
同理BD=,
∴BE=DE+BD=,C'E=BC'+BE=3+=,
∵CE∥A'B,
∴=,
∴=,
∴BM=;
(3)DE存在最小值1,理由如下:
过A作AP∥A'C'交C'D延长线于P,连接A'C,如图:
∵△ABC绕点B顺时针旋转得到△A′BC′,
∴BC=BC',∠ACB=∠A'C'B=90°,AC=A'C',
∴∠BCC'=∠BC'C,
而∠ACP=180°﹣∠ACB﹣∠BCC'=90°﹣∠BCC',
∠A'C'D=∠A'C'B﹣∠BC'C=90°﹣∠BC'C,
∴∠ACP=∠A'C'D,
∵AP∥A'C',
∴∠P=∠A'C'D,
∴∠P=∠ACP,
∴AP=AC,
∴AP=A'C',
在△APD和△A'C'D中,
,
∴△APD≌△A'C'D(AAS),
∴AD=A'D,即D是AA'中点,
∵点E为AC的中点,
∴DE是△AA'C的中位线,
∴DE=A'C,
要使DE最小,只需A'C最小,此时A'、C、B共线,A'C的最小值为A'B﹣BC=AB﹣BC=2,
∴DE最小为A'C=1.
中考强化练习河北省中考数学模拟练习 卷(Ⅱ)(含答案及详解): 这是一份中考强化练习河北省中考数学模拟练习 卷(Ⅱ)(含答案及详解),共31页。试卷主要包含了单项式的次数是,和按如图所示的位置摆放,顶点B,一元二次方程的根为.等内容,欢迎下载使用。
河北省中考数学模拟专项测评 A卷(含答案及详解): 这是一份河北省中考数学模拟专项测评 A卷(含答案及详解),共29页。试卷主要包含了下列计算中,正确的是,下列方程变形不正确的是,如图,E等内容,欢迎下载使用。
2022年河北省中考数学模拟自测卷2(word版含答案): 这是一份2022年河北省中考数学模拟自测卷2(word版含答案),共28页。试卷主要包含了条线段等内容,欢迎下载使用。












