2022年河南省中招模拟考试数学试题(含答案-双向细目表) (2)

这是一份2022年河南省中招模拟考试数学试题(含答案-双向细目表) (2)，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

中招模拟考试数学试题


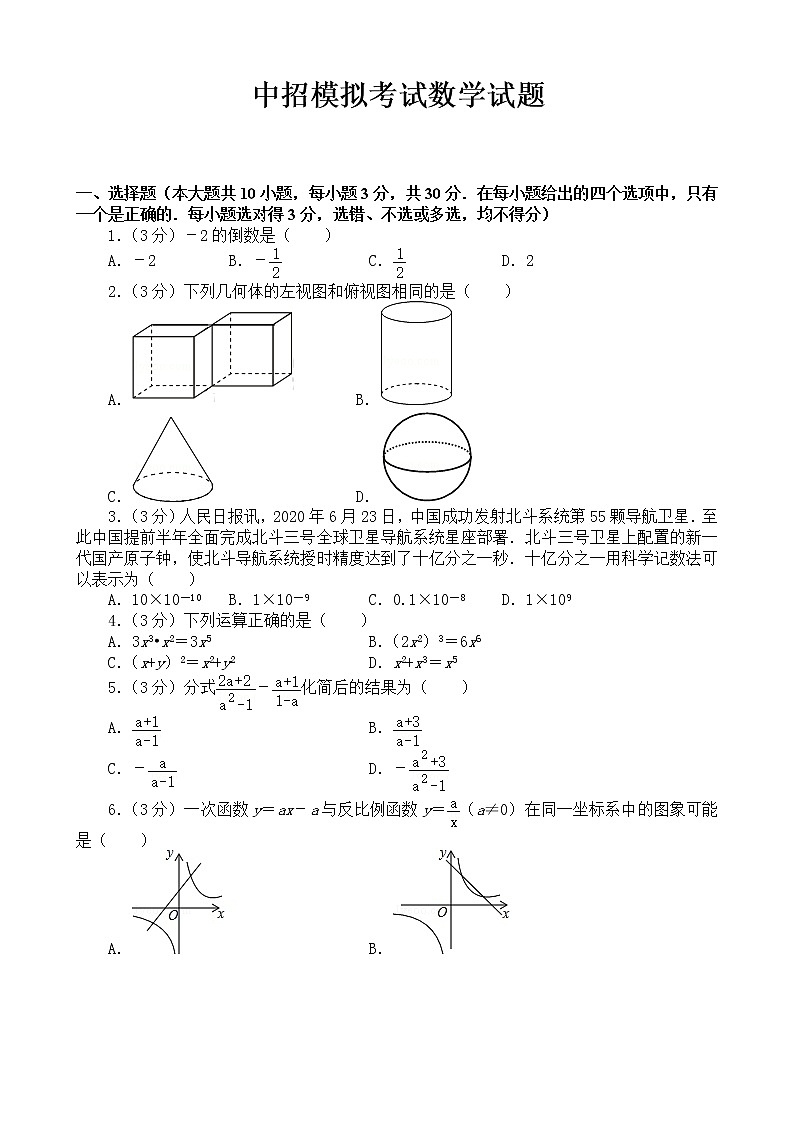
一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个是正确的．每小题选对得3分，选错、不选或多选，均不得分）
1．（3分）－2的倒数是（　　）
A．－2 B．－ C． D．2
2．（3分）下列几何体的左视图和俯视图相同的是（　　）
A． B．
C． D．
3．（3分）人民日报讯，2020年6月23日，中国成功发射北斗系统第55颗导航卫星．至此中国提前半年全面完成北斗三号全球卫星导航系统星座部署．北斗三号卫星上配置的新一代国产原子钟，使北斗导航系统授时精度达到了十亿分之一秒．十亿分之一用科学记数法可以表示为（　　）
A．10×10－10 B．1×10－9 C．0.1×10－8 D．1×109
4．（3分）下列运算正确的是（　　）
A．3x3•x2＝3x5 B．（2x2）3＝6x6
C．（x+y）2＝x2+y2 D．x2+x3＝x5
5．（3分）分式－化简后的结果为（　　）
A． B．
C．－ D．－
6．（3分）一次函数y＝ax－a与反比例函数y＝（a≠0）在同一坐标系中的图象可能是（　　）
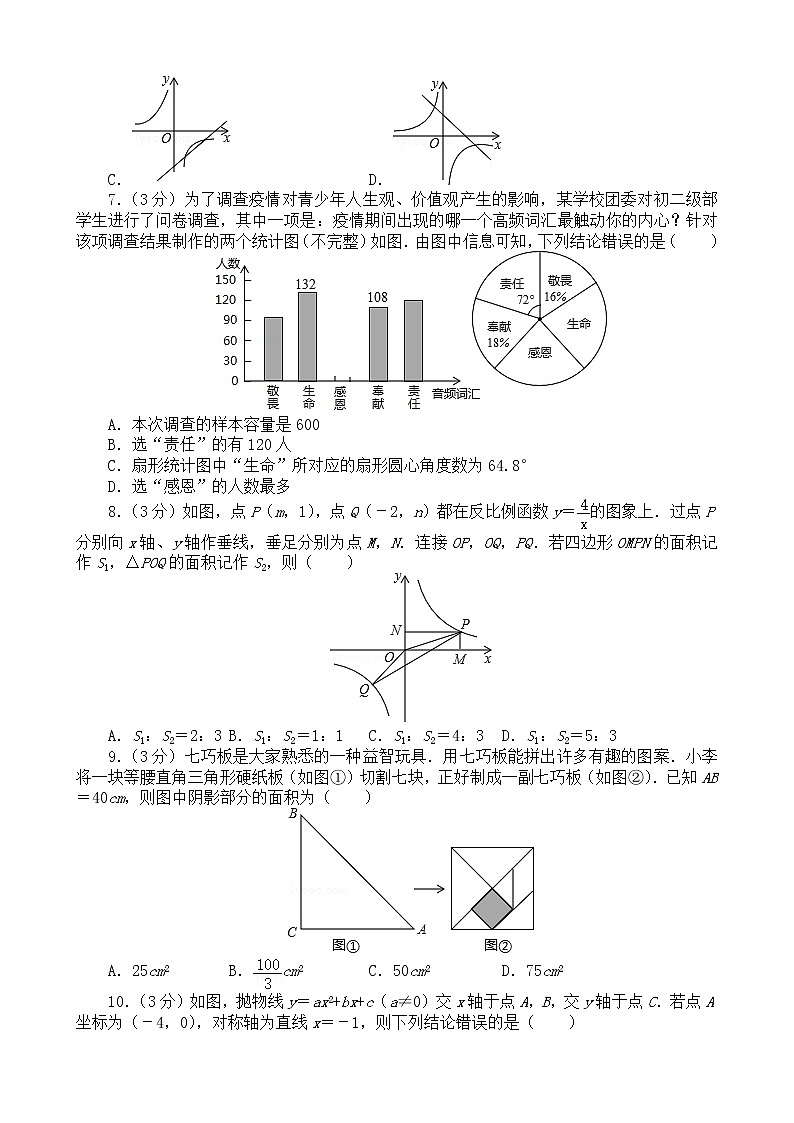
A． B．
C． D．
7．（3分）为了调查疫情对青少年人生观、价值观产生的影响，某学校团委对初二级部学生进行了问卷调查，其中一项是：疫情期间出现的哪一个高频词汇最触动你的内心？针对该项调查结果制作的两个统计图（不完整）如图．由图中信息可知，下列结论错误的是（　　）

A．本次调查的样本容量是600
B．选“责任”的有120人
C．扇形统计图中“生命”所对应的扇形圆心角度数为64.8°
D．选“感恩”的人数最多
8．（3分）如图，点P（m，1），点Q（－2，n）都在反比例函数y＝的图象上．过点P分别向x轴、y轴作垂线，垂足分别为点M，N．连接OP，OQ，PQ．若四边形OMPN的面积记作S1，△POQ的面积记作S2，则（　　）

A．S1：S2＝2：3 B．S1：S2＝1：1 C．S1：S2＝4：3 D．S1：S2＝5：3
9．（3分）七巧板是大家熟悉的一种益智玩具．用七巧板能拼出许多有趣的图案．小李将一块等腰直角三角形硬纸板（如图①）切割七块，正好制成一副七巧板（如图②）．已知AB＝40cm，则图中阴影部分的面积为（　　）

A．25cm2 B．cm2 C．50cm2 D．75cm2
10．（3分）如图，抛物线y＝ax2+bx+c（a≠0）交x轴于点A，B，交y轴于点C．若点A坐标为（－4，0），对称轴为直线x＝－1，则下列结论错误的是（　　）

A．二次函数的最大值为a－b+c
B．a+b+c＞0
C．b2－4ac＞0
D．2a+b＝0
二、填空题（本大题共5小题，每小题3分，共15分．只要求填出最后结果）

11．（3分）计算－－（－1）0的结果是　 　．
12．（3分）一元二次方程4x（x－2）＝x－2的解为　 　．
13．（3分）下表中y与x的数据满足我们初中学过的某种函数关系．其函数表达式为　 　．
x
…
－1
0
1
3
…
y
…
0
3
4
0
…
14．（3分）如图，AC平分∠DCB，CB＝CD，DA的延长线交BC于点E，若∠EAC＝49°，则∠BAE的度数为　 　．

15．（3分）矩形纸片ABCD，长AD＝8cm，宽AB＝4cm，折叠纸片，使折痕经过点B，交AD边于点E，点A落在点A'处，展平后得到折痕BE，同时得到线段BA'，EA'，不再添加其它线段．当图中存在30°角时，AE的长为　 　厘米．


三、解答题（本大题共8小题，共75分）

16．（8分）先化简，再求值：（－）÷，其中x＝．
17．（9分）为积极响应教育部“停课不停学”的号召，某中学组织本校优秀教师开展线上教学，经过近三个月的线上授课后，在五月初复学．该校为了解学生不同阶段学习效果，决定随机抽取八年级部分学生进行两次跟踪测评，第一次是复学初对线上教学质量测评，第二次是复学一个月后教学质量测评．根据第一次测试的数学成绩制成频数分布直方图（图1）．

复学一个月后，根据第二次测试的数学成绩得到如下统计表：
成绩
30≤x＜40
40≤x＜50
50≤x＜60
60≤x＜70
70≤x＜80
80≤x＜90
90≤x≤100
人数
1
3
3
8
15
m
6
根据以上图表信息，完成下列问题：
（1）m＝　 　；
（2）请在图2中作出两次测试的数学成绩折线图，并对两次成绩作出对比分析（用一句话概述）；
（3）某同学第二次测试数学成绩为78分．这次测试中，分数高于78分的至少有　 　人，至多有　 　人；
（4）请估计复学一个月后该校800名八年级学生数学成绩优秀（80分及以上）的人数．

18．（9分）如图，Rt△ABC中，∠ACB＝90°，顶点A，B都在反比例函数y＝（x＞0）的图象上，直线AC⊥x轴，垂足为D，连结OA，OC，并延长OC交AB于点E，当AB＝2OA时，点E恰为AB的中点，若∠AOD＝45°，OA＝2．
（1）求反比例函数的解析式；
（2）求∠EOD的度数．




19．（9分）如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图．量得托板长AB＝120mm，支撑板长CD＝80mm，底座长DE＝90mm．托板AB固定在支撑板顶端点C处，且CB＝40mm，托板AB可绕点C转动，支撑板CD可绕点D转动．（结果保留小数点后一位）
（1）若∠DCB＝80°，∠CDE＝60°，求点A到直线DE的距离；
（2）为了观看舒适，在（1）的情况下，把AB绕点C逆时针旋转10°后，再将CD绕点D顺时针旋转，使点B落在直线DE上即可，求CD旋转的角度．（参考数据：sin40°≈0.643，cos40°≈0.766，tan40°≈0.839，sin26.6°≈0.448，cos26.6°≈0.894，tan26.6°≈0.500，≈1.732）

20.（9分）如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E。
（1）若∠B＝70°，求∠CAD的度数；
（2）若AB＝4，AC＝3，求DE的长。


21.（10分） 某超市计划购进一批甲、乙两种玩具，已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元，2件甲种玩具的进价与3件乙种玩具的进价的和为141元。
（1）求每件甲种、乙种玩具的进价分别是多少元？
（2）如果购进甲种玩具有优惠，优惠方法是：购进甲种玩具超过20件，超出部分可以享受7折优惠，若购进x（x＞0）件甲种玩具需要花费y元，请你求出y与x的函数关系式；
（3）在（2）的条件下，超市决定在甲、乙两种玩具中选购其中一种，且数量超过20件，请你帮助超市判断，购进哪种玩具省钱。

22．（10分）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c与x轴交于点A（﹣2，0），点B（4，0），与y轴交于点C（0，8），连接BC．又已知位于y轴右侧且垂直于x轴的动直线l，沿x轴正方向从O运动到B（不含O点和B点），且分别交抛物线、线段BC以及x轴于点P，D，E．
（1）求抛物线的表达式；
（2）连接AC，AP，当直线l运动时，求使得△PEA和△AOC相似的点P的坐标；
（3）作PF⊥BC，垂足为F，当直线l运动时，求Rt△PFD面积的最大值．

23.（11分）如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E．
（1）如图1，猜想∠QEP=________°；
（2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；
（3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长。








参考答案

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个是正确的．每小题选对得3分，选错、不选或多选，均不得分）
1．B
【解答】解：∵－2×＝1．
∴－2的倒数是－．
2．D
【解答】解：选项A中的几何体的左视图和俯视图为：

选项B中的几何体的左视图和俯视图为：

选项C中的几何体的左视图和俯视图为：

选项D中的几何体的左视图和俯视图为：

因此左视图和俯视图相同的是选项D中的几何体．
3．B
【解答】解：∵十亿分之一＝＝1×10－9，
∴十亿分之一用科学记数法可以表示为：1×10－9．
4．A
【解答】解：A.3x3•x2＝3x5，故本选项符合题意；
B．（2x2）3＝8x6，故本选项不合题意；
C．（x+y）2＝x2+2xy+y2，故本选项不合题意；
D．x2与x3不是同类项，所以不能合并，故本选项不合题意．
5．B
【解答】解：－
＝
＝
＝
＝
＝
＝．
6．D
【解答】解：A、由函数y＝ax－a的图象可知a＞0，－a＞0，由函数y＝（a≠0）的图象可知a＞0，矛盾，错误；
B、由函数y＝ax－a的图象可知a＜0，由函数y＝（a≠0）的图象可知a＞0，相矛盾，故错误；
C、由函数y＝ax－a的图象可知a＞0，由函数y＝（a≠0）的图象可知a＜0，故错误；
D、由函数y＝ax－a的图象可知a＜0，－a＞0，由函数y＝（a≠0）的图象可知a＜0，故正确．
7．C
【解答】解：本次调查的样本容量为：108÷18%＝600，故选项A中的说法正确；
选“责任”的有600×＝120（人），故选项B中的说法正确；
扇形统计图中“生命”所对应的扇形圆心角度数为360°×＝79.2°，故选项C中的说法错误；
选“感恩”的人数为：600－132－600×（16%+18%）－120＝144，故选“感恩”的人数最多，故选项D中的说法正确．
8．C
【解答】解：点P（m，1），点Q（－2，n）都在反比例函数y＝的图象上．
∴m×1＝－2n＝4，
∴m＝4，n＝－2，
∴P（4，1），Q（－2，－2），
，∴S1＝4，
作QK⊥PN，交PN的延长线于K，
则PN＝4，ON＝1，PK＝6，KQ＝3，
∴S2＝S△PQK－S△PON－S梯形ONKQ＝－－（1+3）×2＝3，
∴S1：S2＝4：3．

9．C
【解答】解：如图：设OF＝EF＝FG＝x（cm），

∴OE＝OH＝2x，
在Rt△EOH中，EH＝2x，
由题意EH＝20cm，
∴20＝2x，
∴x＝5，
∴阴影部分的面积＝（5）2＝50（cm2）
10．D
【解答】解：当x＝－1时，y＝a－b+c的值最大，选项A不符合题意；
抛物线与x轴的另一个交点为（2，0），
当x＝1时，y＝a+b+c＞0，因此选项B不符合题意；
抛物线与x轴有两个不同交点，因此b2－4ac＞0，故选项C不符合题意；
抛物线y＝ax2+bx+c过点A（－4，0），对称轴为直线x＝－1，
因此有：x＝－1＝－，即2a－b＝0，因此选项D符合题意．
二、填空题（本大题共6小题，每小题3分，共18分．只要求填出最后结果）
11．
【解答】解：－－（－1）0
＝
＝．
12． x1＝2，x2＝
【解答】解：4x（x－2）＝x－2
4x（x－2）－（x－2）＝0
（x－2）（4x－1）＝0
x－2＝0或4x－1＝0
解得x1＝2，x2＝．
13． y＝－x2+2x+3
【解答】解：根据表中y与x的数据设函数关系式为：y＝ax2+bx+c，
将表中（1，4）、（－1，0）、（0，3）代入函数关系式，得
∴，
解得，
∴函数表达式为y＝－x2+2x+3．
当x＝3时，代入y＝－x2+2x+3＝0，
∴（3，0）也适合所求得的函数关系式．

14． 82°
【解答】解：∵AC平分∠DCB，
∴∠BCA＝∠DCA，
又∵CB＝CD，AC＝AC，
∴△ABC≌△ADC（SAS），
∴∠B＝∠D，
∴∠B+∠ACB＝∠D+∠ACD，
∵∠CAE＝∠D+∠ACD＝49°，
∴∠B+∠ACB＝49°，
∴∠BAE＝180°－∠B－∠ACB－∠CAE＝82°．
15． 厘米或4厘米或（8－4）厘米
【解答】解：
①当∠ABE＝30°时，AE＝AB×tan30°＝；
②当∠AEB＝30°时，AE＝＝＝4；
③∠ABE＝15°时，∠ABA′＝30°，延长BA′交AD于F，如下图所示，

设AE＝x，则EA′＝x，EF＝，
∵AF＝AE+EF＝ABtan30°＝，
∴x+＝，
∴x＝8－4，
∴AE＝8－4．
三、解答题（本大题共8小题，共75分．）

16．【分析】先根据分式的混合运算顺序和运算法则化简原式，再将x的值代入计算可得．
【解答】解：原式＝[－]÷
＝•
＝（5分）
当x＝时，
原式＝＝．（8分）
17．【分析】（1）根据前后两次抽取的人数一样多，可以计算出m的值；
（2）根据直方图中的数据和表格中的数据，可以将图2中的图补充完整，然后即可写出成绩的变化情况；
（3）根据表格中的数据，可以得到分数高于78分的至少有多少人，至多有多少人；
（4）根据表格中的数据，可以计算出复学一个月后该校800名八年级学生数学成绩优秀（80分及以上）的人数．
【解答】解：（1）m＝（2+8+10+15+10+4+1）－（1+3+3+8+15+6）＝14
故答案为：14；（2分）
（2）折线图如下图所示，

复学后，学生的成绩总体上有了明显的提升；（4分）
（3）某同学第二次测试数学成绩为78分．这次测试中，分数高于78分的至少有14+6＝20（人），至多有14+6+（15－1）＝34（人），
故答案为：20，34；（6分）
（4）800×＝320（人），
答：复学一个月后该校800名八年级学生数学成绩优秀（80分及以上）的有320人（9分）
18．【分析】（1）根据题意求得A（2，2），然后代入y＝（x＞0），求得k的值，即可求得反比例函数的解析式；
（2）根据AB＝2OA时，点E恰为AB的中点，得出OA＝AE＝BE，根据直角三角形斜边中线的性质得出CE＝AE＝BE，根据等腰三角形的性质以及三角形外角的性质即可得出∠AOE＝2∠EOD，从而求得∠EOD＝15°
【解答】解：（1）∵直线AC⊥x轴，垂足为D，∠AOD＝45°，
∴△AOD是等腰直角三角形，
∵OA＝2，
∴OD＝AD＝2，
∴A（2，2），
∵顶点A在反比例函数y＝（x＞0）的图象上，
∴k＝2×2＝4，
∴反比例函数的解析式为y＝；（4分）
（2）∵AB＝2OA，点E恰为AB的中点，
∴OA＝AE，
∵Rt△ABC中，∠ACB＝90°，
∴CE＝AE＝BE，
∴∠AOE＝∠AEO，∠ECB＝∠EBC，
∵∠AEO＝∠ECB+∠EBC＝2∠EBC，
∵BC∥x轴，
∴∠EOD＝∠ECB，
∴∠AOE＝2∠EOD，
∵∠AOD＝45°，
∴∠EOD＝15°（9分）
．
19．【分析】（1）通过作垂线，构造直角三角形，利用直角三角形的边角关系，求出CB、AF，即可求出点A到直线DE的距离；
（2）画出旋转后的图形，结合图形，明确图形中的已知的边角，再利用直角三角形的边角关系求出相应的角度即可．
【解答】解：（1）如图2，过A作AM⊥DE，交ED的延长线于点M，过点C作CF⊥AM，垂足为F，过点C作CN⊥DE，垂足为N，

由题意可知，AC＝80，CD＝80，∠DCB＝80°，∠CDE＝60°，
在Rt△CDN中，CN＝CD•sin∠CDE＝80×＝40 （mm）＝FM，
∠DCN＝90°－60°＝30°，
又∵∠DCB＝80°，
∴∠BCN＝80°－30°＝50°，
∵AM⊥DE，CN⊥DE，
∴AM∥CN，
∴∠A＝∠BCN＝50°，
∴∠ACF＝90°－50°＝40°，
在Rt△AFC中，AF＝AC•sin40°＝80×0.643≈51.44，
∴AM＝AF+FM＝51.44+40≈120.7（mm），
答：点A到直线DE的距离约为120.7mm；（5分）
（2）旋转后，如图3所示，根据题意可知∠DCB＝80°+10°＝90°，

在Rt△BCD中，CD＝80，BC＝40，
∴tan∠D＝＝＝0.500，
∴∠D＝26.6°，
因此旋转的角度为：60°－26.6°＝33.4°，
答：CD旋转的角度约为33.4°．（9分）
20. 解：（1）∵AB是半圆O的直径，∴∠ACB＝90°，又∵OD∥BC，∴∠AEO＝90°，即OE⊥AC，∠CAB＝90°－∠B＝90°－70°＝20°∠AOD＝∠B＝70°。∵OA＝OD，∴∠DAO＝∠ADO＝＝55°，∴∠CAD＝∠DAO－∠CAB＝55°－20°＝35°；（5分）
（2）在直角△ABC中，BC＝＝∵OE⊥AC，∴AE＝EC，又∵OA＝OB，∴OE＝BC＝又∵OD＝AB＝2，∴DE＝OD－OE＝2－（9分）
21. 解：（1）设每件甲种玩具的进价是x元，每件乙种玩具的进价是y元，由题意得，解得，答：每件甲种玩具的进价是30元，每件乙种玩具的进价是27元；（3分）
（2）当0＜x≤20时，y＝30x；当x＞20时，y＝20×30＋（x－20）×30×0.7＝21x＋180；（6分）
（3）设购进玩具x件（x＞20），则乙种玩具消费27x元；
当27x＝21x＋180，则x＝30，所以当购进玩具正好30件，选择购其中一种即可；当27x＞21x＋180，则x＞30，所以当购进玩具超过30件，选择购甲种玩具省钱；当27x＜21x＋180，则x＜30，所以当购进玩具少于30件，选择购乙种玩具省钱。（10分）
22．解：（1）将点A、B、C的坐标代入二次函数表达式得：，解得：，
故抛物线的表达式为：y＝﹣x2+2x+8；（3分）

（2）∵点A（﹣2，0）、C（0，8），
∴OA＝2，OC＝8，
∵l⊥x轴，
∴∠PEA＝∠AOC＝90°，
∵∠PAE≠∠CAO，
∴只有当∠PAE＝∠ACO时，△PEA∽△AOC，
此时，即：，
∴AE＝4PE，
设点P的纵坐标为k，则PE＝k，AE＝4k，
∴OE＝4k﹣2，
将点P坐标（4k﹣2，k）代入二次函数表达式并解得：
k＝0或（舍去0），
则点P（，）；（7分）

（3）在Rt△PFD中，∠PFD＝∠COB＝90°，
∵l∥y轴，∴∠PDF＝∠OCB，∴Rt△PFD∽Rt△OCB，
∴，
∴S△PDF＝•S△BOC（10分）

23. （1）60°（2分）
∵△ABC是等边三角形，∴AC=BC，∠ACB=60°．又由题意可知，CP=CQ，∠PCQ=6O°，
∴∠ACP=∠BCQ，∴△ACP≌△BCQ，∴∠APC=∠Q，又∵∠PME=∠QMC，∴∠QEP=∠PCQ=6O°
（2）60°
以∠DAC是锐角为例证明如下:
∵△ABC是等边三角形，∴AC=BC，∠ACB=60°，又由题意可知，CP=CQ，∠PCQ=6O°，∴∠ACP=∠BCQ，∴△ACP≌△BCQ，∴∠APC=∠Q，
又∵∠POE=∠QOC，∴∠QEP=∠PCQ=6O°。（7分）
（3）连接C Q，作CHAD于H，如图3，与（2）一样可证△ACP≌△BCQ， ∴AP=BQ，
∵∠DAC=135°，∠ACP=15°，∴∠APC=30°，∠PCB=45°，∴△ACH为等腰直角三角形，
∴AH=CH=AC=,在Rt△PCH中，PH=CH=，∴PA=PH-AH=-,∴BQ=-。（11分）








数学 学科中考模拟天府师大






试卷
双向细目表
题 号
题型
分值
考查知识点
目标层次
预估难度
识记
理解
应用
分析
综合
易
中
难
一
1
选择题
3分
实数、有理数、无理数
√




√


2
选择题
3分
三视图
√




√


3
选择题
3分
科学计数法
√




√


4
选择题
3分
幂的乘方
√




√


5
选择题
3分
分式

√



√


6
选择题
3分
反比例函数与一次函数性质图像



√


√

7
选择题
3分
抽样调查适用范围


√


√


8
选择题
3分
函数与几何图形




√

√

9
选择题
3分
阴影部分的面积




√


√
10
选择题
3分
二次函数图像




√


√
二
11
填空题
3分
数与式

√




√

12
填空题
3分
解一元二次方程
√




√


13
填空题
3分
函数表达式


√


√


14
填空题
3分
角



√


√

15
填空题
3分
矩形、翻转相关性质




√


√
三
16
计算题
8分
分式的化简求值


√


√


17
计算题
9分
统计图数据分析


√


√


18
综合题
9分
函数与几何图形综合运用




√
√


19
综合题
9分
利用三角函数解决实际问题




√

√

20
综合题
9分
圆的综合运用




√

√

21
综合题
10分
实际问题的最优方案




√

√

22
综合题
10分
二次函数与几何图形相结合




√


√
23
综合题
11分
旋转相似的类比延伸




√


√

说明：
1、 题号指大题（部分）、小题序号，此项可根据试卷结构自行调整。
2、题型包括：填空题、选择题、计算题、简答题、综合题等，根据学科有所区别。
3、目标层次：请依据学科标准要求填写，使用通用能力层级“识记、理解、应用、分析、综合”。请用√符号表示。
4、试题来源包括：原创题、教材原题、教材改编题、教案原题、教案改编题、中考原题、网上下载等。
5、注：难度指标要点
容易题（0.90-0.75） 较易题（0.70左右） 较难题（0.55左右） 难题（0.45-0.20）