2022年山东省青岛市崂山区九年级数学一模试题（附答案）

 九年级数学一模试题

一、单选题

1．下列四个数字，相反数最大的是（　　）

A．4 B．-4 C． D．

2．下列四个图形，是轴对称图形的是（　　）

A． B．

C． D．

3．2021年崂山区经济高质量发展势头强劲，区级一般公共预算收入200.2亿元，同比增长23.7%，这是崂山区一般公共预算收入首次跨越200亿大关，10年来首次实现20%以上的递增．“200.2亿”用科学记数法可表示为（　　）

A．2.002×1010 B．2.002×109

C．0.2002×1010 D．2002×108

4．下列立体图形中．主视图是圆的是（　　）

A． B． C． D．

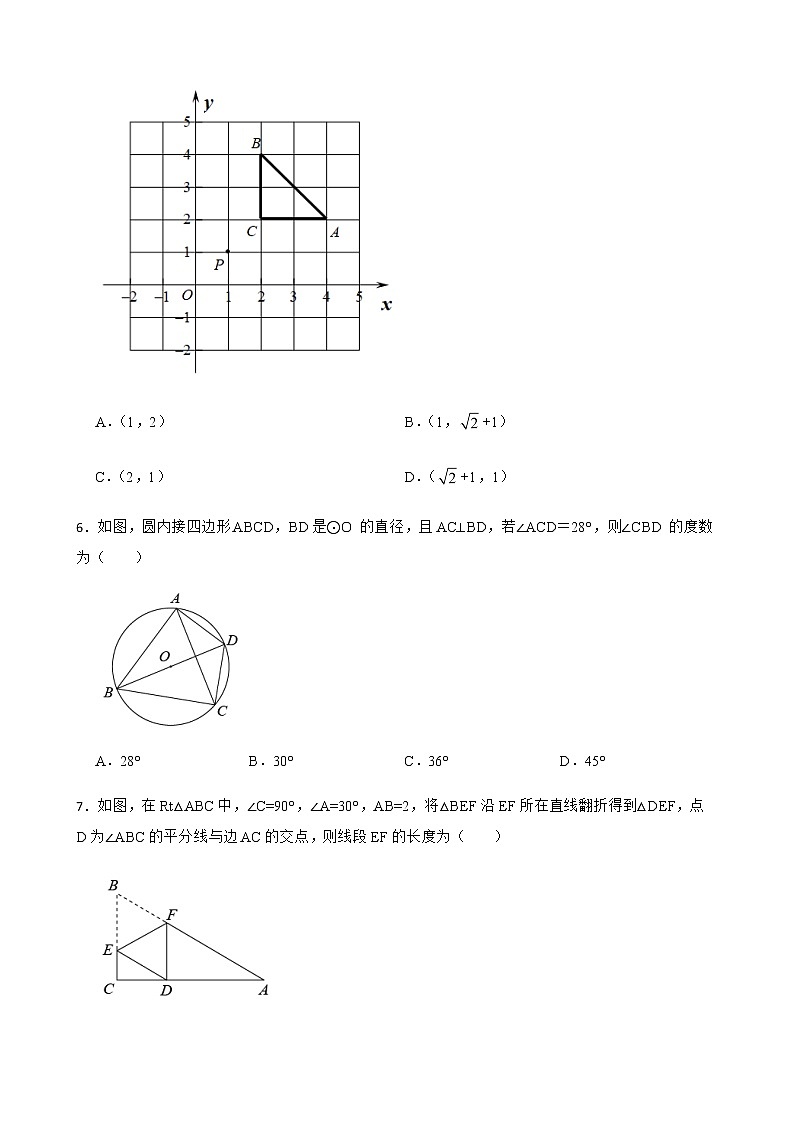
5．如图，将△ABC 绕点P按逆时针方向旋转45°，得到△A′B′C′，则点C的对应点C′的坐标是（　　）

A．（1，2） B．（1，+1）

C．（2，1） D．（+1，1）

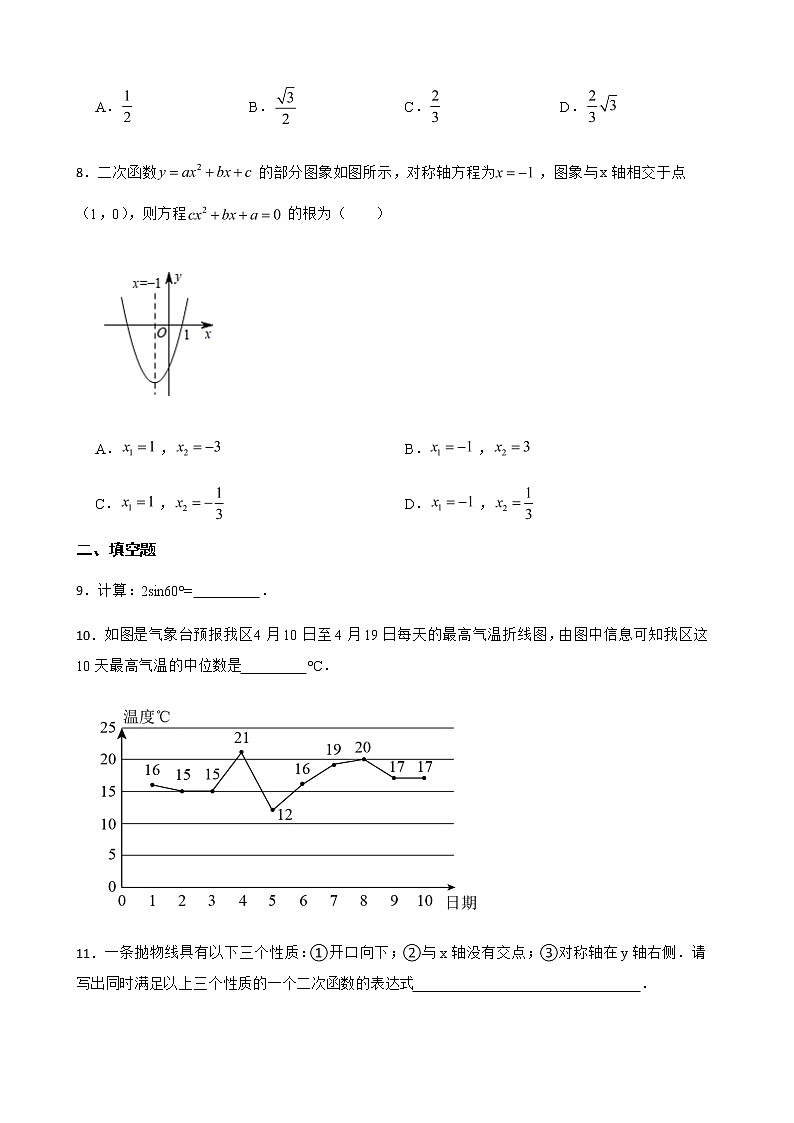
6．如图，圆内接四边形ABCD，BD是⊙O 的直径，且AC⊥BD，若∠ACD＝28°，则∠CBD 的度数为（　　）

A．28° B．30° C．36° D．45°

7．如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=2，将△BEF沿EF所在直线翻折得到△DEF，点D为∠ABC的平分线与边AC的交点，则线段EF的长度为（　　）

A． B． C． D．

8．二次函数的部分图象如图所示，对称轴方程为，图象与x轴相交于点（1，0），则方程的根为（　　）

A．， B．，

C．， D．，

二、填空题

9．计算：2sin60°=　     　．

10．如图是气象台预报我区4月10日至4月19日每天的最高气温折线图，由图中信息可知我区这10天最高气温的中位数是　     　°C．

11．一条抛物线具有以下三个性质：①开口向下；②与x轴没有交点；③对称轴在y轴右侧．请写出同时满足以上三个性质的一个二次函数的表达式　                           　．

12．如图所示，反比例函数的图象过正方形OABC对角线OB中点F，则B点坐标为　         　．

13．如图，在正方形ABCD中，AB=4，E、F分别为边AB、BC中点，连接DE、AF相交于点G，则△AGE的面积为　     　．

14．如图，在平行四边形ABCD中，AD=8，AB=4，∠BAD=60°，E为AD上一点，以点E为圆心，以ED的长为半径作弧与BC相切于点H，点F为线段AB中点，则阴影部分面积为　           　．

三、解答题

15．已知：△ABC．求作：⊙O ，使圆心在边AB上，且与边AC、BC所在直线相切．

16．计算：

（1）计算：；

（2）解不等式组： ．

17．2022年北京冬奥会的吉祥物“冰墩墩”与“雪容融”，现有吉祥物“冰墩墩”与“雪容融”各一份给小明与小华．两人都想要“冰墩墩”，现用如图所示A、B两个转盘进行配色游戏，A盘是四等分，B盘是三等分，其中一个转出红色另一个转出蓝色即可配成紫色．分别转动两个转盘（指针指向分界线则重新转动转盘），配色是紫色时将“冰墩墩”给小明，否则就给小华．请用列表或画树状图的方法说明这个游戏是否公平．

18．如图，某数学活动小组进行综合实践活动测量学校旗杆AB的高度，从旗杆正前方米处的点C出发，沿斜面坡度i=1：的斜坡CD前进4米到达点D，在点D处安置测角仪，测得旗杆顶端A的仰角为37°，仪器的高DE为1.5米．已知点A、B、C、D、E、M在同一平面内，∠DCM=30°，AB⊥BC，AB//DE．求旗杆AB的高度．

（参考数据：sin37°，cos37°，tan37°，计算结果保留根号）

19．某校抽取部分学生参加“森林防火”知识竞赛，按成绩分为A、B、C、D、E五个等级，并绘制了如下条形统计图和扇形统计图．

请根据图中信息解答下列问题：

（1）补全频数条形图；

（2）求出扇形统计图中的百分比a、b；

（3）参加抽样的学生占全校学生的16%，请估计全校学生的总数．

20．A、B两地相距19.2km，甲、乙两人相向而行，两人的运动速度保持不变。甲从A地向B地出发，当甲运动一段时间后，乙从B地向A地出发，甲、乙两人同时运动时他们之间的距离y（km）与乙运动时间t（h）满足一次函数关系式，其图象如图所示．

（1）根据图像求y与t的函数关系式，并求出两人的速度和；

（2）已知甲由A地运动到B地所用时间是乙由B地运动到A地所用时间的倍．求甲由A地运动到B地所用时间是多少小时？

21．如图，正方形ABCD，点P在边BC的延长线上，连接AP交BD于点F，过点C作CG//AP交BD于点G，连接AG、CF．

（1）求证：△ADF≌△CBG；

（2）判断四边形AGCF是什么特殊四边形？请说明理由．

22．某市在党中央实施“精准扶贫”政策的号召下，大力开展科技扶贫工作，帮助农民组建农副产品销售公司，某农副产品的年产量不超过100万件，该产品的生产费用y（万元）与年产量x（万件）之间的函数图象是顶点为原点的抛物线的一部分（如图①所示）；该产品的销售单价z（元/件）与年销售量x（万件）之间的函数图象是如图②所示的一条线段，生产出的产品都能在当年销售完，达到产销平衡，所获毛利润为w万元．（毛利润＝销售额﹣生产费用）

（1）请直接写出y与x以及z与x之间的函数关系式；  

（2）求w与x之间的函数关系式；并求年产量多少万件时，所获毛利润最大？最大毛利润是多少？  

（3）由于受资金的影响，今年投入生产的费用不会超过360万元，今年最多可获得多少万元的毛利润？  

23．实际问题：

各边长都是整数，最大边长为31的三角形有多少个？

问题建模：为解决上面的数学问题，我们先研究下面的数学模型。

在1～n这n个自然数中，每次取两个数（可重复），使得所取的两个数之和大于n，有多少种不同的取法？

为了找到解决问题的方法，我们把上面数学模型简单化．

探究一：

在1～4这4个自然数中，每次取两个数（可重复），使得所取的两个数之和大于4，有多少种不同的取法？

第一步：在1～4这4个自然数中，每次取两个不同的数，使得所取的两个数之和大于4，根据题意，有下列取法：1+4，2+3，2+4，3+2，3+4，4+1，4+2，4+3；而1+4与4+1，2+3与3+2，…是同一种取法，所有上述每一种取法都重复过一次，因此共有种不同的取法．

第二步：在1～4这4个自然数中，每次取两个相同的数，使得所取的两个数之和大于4，有下列取法：3+3，4+4，因此有2种不同的取法．

综上所述，在1～4这4个自然数中，每次取两个数（可重复），使得所取的两个数之和大于4，有种不同的取法．

探究二：

在1～5这5个自然数中，每次取两个数（可重复），使得所取的两个数之和大于5，有多少种不同的取法？

第一步：在1～5这5个自然数中，每次取两个不同的数，使得所取的两个数之和大于5，根据题意，有下列取法：1+5，2+4，2+5，3+4，3+5，4+2，4+3，4+5，5+1，5+2，5+3，5+4；而1+5与5+1，2+4与4+2，…是同一种取法，所有上述每一种取法都重复过一次，因此共有种不同的取法．

第二步：在1～5这5个自然数中，每次取两个相同的数，使得所取的两个数之和大于5，有下列取法：3+3，4+4，5+5因此有3种不同的取法．

综上所述，在1～5这5个自然数中，每次取两个数（可重复），使得所取的两个数之和大于5，有种不同的取法．

探究三：

在1～6这6个自然数中，每次取两个数（可重复），使得所取的两个数之和大于6，有多少种不同的取法？（仿照探究二写出探究过程）

探究四：

在1～7这7个自然数中，每次取两个数（可重复），使得所取的两个数之和大于7，有      ▲ 种不同的取法．

探究五：

在1～n（n为偶数）这n个自然数中，每次取两个数（可重复），使得所取的两个数之和大于n，有      ▲ 种不同的取法．

探究六：

在1～n（n为奇数）这n个自然数中，每次取两个数（可重复），使得所取的两个数之和大于n，有      ▲ 种不同的取法．

问题解决：

①各边长都是整数，最大边长为20的三角形有      ▲ 个；

②各边长都是整数，最大边长为31的三角形有      ▲ 个．

24．如图，正方形ABCD，AB=4cm，点P在线段BC的延长线上．点P从点C出发，沿BC方向运动，速度为2cm/s；点Q从点A出发，沿AB方向运动，速度为1cm/s．连接PQ，PQ分别与BD、CD相交于点E、F．设运动时间为t（s）（0＜t＜4）．

解答下列问题：

（1）线段CF长为多少时，点F为线段PQ中点？

（2）当t为何值时，点E在对角线BD中点上？

（3）当PQ中点在∠DCP平分线上时，求t的值；

（4）设四边形BCFE的面积为S（），求S与t的函数关系式．

答案解析部分

1．【答案】B

2．【答案】D

3．【答案】A

4．【答案】D

5．【答案】B

6．【答案】A

7．【答案】C

8．【答案】C

9．【答案】

10．【答案】16.5

11．【答案】（答案不唯一）

12．【答案】（2，2）

13．【答案】

14．【答案】

15．【答案】解：如图，作∠ACB的角平分线CO，过点O作OD⊥BC于D，以O为圆心，OD为半径作⊙O，⊙O即为所求．

16．【答案】（1）解：

=

=

=；

（2）解：，

解不等式组，得，

∴不等式组的解集为；

17．【答案】解：画树状图如下，一共有12种等可能性，

其中配成紫色的可能性有7种，

概率为，

不是紫色的概率为，

∵，

∴游戏不公平．

18．【答案】解：如图，过点E作于F，延长ED交BM于点G．

根据作图结合题意可知四边形为矩形，

∴BF=EG，BG=EF．

根据题意可知米，米，米，．

∵在中，，

∴米，

米，

∴米，米．

∵在中，，

∴米，

∴米．

答：旗杆AB的高度为米．

19．【答案】（1）解：抽取的学生总数为10÷12.5%=80（人），

成绩为C等级的人数为80×25%=20（人），

故补全条形统计图如下：

（2）解：．

（3）解：80÷16%=500（人）．

答：估计全校学生的总数约为500人．

20．【答案】（1）解：设y与t的函数关系式为，则

，解得，

∴y与t的函数关系式为；

两人的速度和为：（km/h）；

（2）解：设甲的速度为，乙的速度为，则

，

由（1）可知，

解得：，；

经检验，，是原方程的解；

∴甲由A地运动到B地所用时间是（小时）；

21．【答案】（1）证明：∵四边形ABCD是正方形，

∴AD∥BC，AD=BC，

∴∠ADB=∠CBD，

∵GC∥AP，

∴∠GCB=∠P，

∴AD∥BP，

∴∠DAF=∠P，

∴∠GCB=∠DAF，

在△ADF和△CBG中，

，

∴ΔADF≌CBG（ASA）；

（2）解：四边形AGCF为菱形，

∵ΔADF≌CBG，

∴AF=CG

又∵AF∥CG

∴四边形AGCF为平行四边形，

连接AC，

∵四边形ABCD为正方形，

∴AC⊥BD，

∴四边形AGCF是菱形．

22．【答案】（1）解：图①可得函数经过点（100，1000）， 

设抛物线的解析式为y=ax2（a≠0），

将点（100，1000）代入得：1000=10000a，

解得：a= ，

故y与x之间的关系式为y= x2．

图②可得：函数经过点（0，30）、（100，20），

设z=kx+b，则

解得： 

故z与x之间的关系式为z=﹣ x+30

（2）解：W=zx﹣y=﹣ x2+30x﹣ x2

=﹣ x2+30x

=﹣ （x2﹣150x）

=﹣ （x﹣75）2+1125，

∵﹣ ＜0，

∴当x=75时，W有最大值1125，

∴年产量为75万件时毛利润最大，最大毛利润为1125万元

（3）解：令y=360，得 x2=360，  

解得：x=±60（负值舍去），

由图象可知，当0＜y≤360时，0＜x≤60，

由W=﹣ （x﹣75）2+1125的性质可知，

当0＜x≤60时，W随x的增大而增大，

故当x=60时，W有最大值1080，

答：今年最多可获得毛利润1080万元．

23．【答案】解：根据题意，可得：探究三：根据题意，有下列取法：1+6，2+5，2+6，3+4，3+5，3+6，4+3，4+5，4+6，5+2，5+3，5+4，5+6，6+1，6+2，6+3，6+4，6+5；而1+6与6+1，2+5与5+2，…是同一种取法，所以上述每一种取法都重复过一次，因此共有种不同的取法；探究四：；探究五：；探究六：；问题解决：①100；②240；

24．【答案】（1）解：如图1，

∵四边形ABCD是正方形，

∴AB=BC=CD=DA=4，CFAB，

∴PF：FQ=PC：CB，

∵PF=FQ，

∴PC=BC=4，

∴2t=4，

解得t=2，

∴AQ=t=2，

∴BQ=4-t=2，

∵CF是△PBQ的中位线，

∴CF=BQ=1．

（2）解：如图2，

∵四边形ABCD是正方形，

∴AB=BC=CD=DA=4，DFAB，

∴BE：ED=BQ：DF，

∵BE=DE，

∴BQ=DF，

∴CF=AQ=t，

∴tanP=，

解得t=1，

∴当t=1s时，点E在对角线BD中点上．

（3）解：如图3，

∵四边形ABCD是正方形，

∴AB=BC=CD=DA=4，∠B=∠DCP=90°，

设CG是∠DCP的平分线，且点G是PQ的中点，

如图3，过点G作GH⊥PB，垂足为H，

则GHAB，

∴QG：GP=BH：HP，

∵QG=GP，∠FCG=∠HCG=45°，

∴BH=PH，GH=CH=，

∵AQ=t，CP=2t，BC=4，

∴GH=CH=，PB=2BH=4+2t，BH=BC+CH=4+，

∴4+2t=2[4+]=12-t，

解得t=，

∴当t=s时，PQ中点在∠DCP平分线上．

（4）解：如图，过点E作GH垂直CD，垂足为G，交AB于点H，

∵∠HBC=∠BCG=∠CGH=90°，

∴四边形BCGH是矩形，

∴GH=BC=4，

∵四边形ABCD是正方形，

∴AB=BC=CD=DA=4，CFAB，

∴CF：BQ=PC：PB，

∵AQ=t，PC=2t，BC=4，

∴BQ=4-t，PB=4+2t，

∴CF=，DF=DC-CF=4-=，

∵CFAB，

∴△BQE∽△DFE，

∴，

∴，

∴，

∴，

∴

=8-

=．