2020-2021学年浙江省绍兴市诸暨市高二（下）期末数学试卷

这是一份2020-2021学年浙江省绍兴市诸暨市高二（下）期末数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年浙江省绍兴市诸暨市高二（下）期末数学试卷
一、选择题（每小题4分，共40分）
1．（4分）已知集合A，则A∩B＝（　　）
A． B． C． D．
2．（4分）已知i为虚数单位，复数z＝i3•（1+i），则|z|＝（　　）
A．1 B． C．2 D．
3．（4分）已知空间直角坐标系中，O为坐标原点，P的坐标为（1，2，3），则（　　）
A．P到原点O的距离是 B．P到平面xOy的距离是1
C．P到平面xOy的距离是2 D．P到平面xOy的距离是3
4．（4分）以直线ax﹣y﹣3﹣a＝0（a∈R）经过的定点为圆心，2为半径的圆的方程是（　　）
A．x2+y2﹣2x+6y+6＝0 B．x2+y2+2x﹣6y+6＝0
C．x2+y2+6x﹣2y+6＝0 D．x2+y2﹣6x+2y+6＝0
5．（4分）已知a，b∈R+，则“lna•lnb＞0”是“（a﹣1）•（b﹣1）＞0”的（　　）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
6．（4分）将函数的图象向右平移φ个单位与函数g（x）＝cos2x的图像重合，则φ可以是（　　）
A． B． C． D．
7．（4分）若函数f（x）＝x2（x﹣a）（x﹣2）在x＝0处取得极大值，则实数a的取值范围是（　　）
A．（﹣∞，0） B．（0，+∞） C．（0，2） D．（2，+∞）
8．（4分）已知F1，F2为双曲线1（a＞0，b＞0）的左、右焦点，过F1作yx的垂线分别交双曲线的左、右两支于B，C两点（如图）．若∠CBF2＝∠CF2B，则双曲线的渐近线方程为（　　）

A．y＝±x B．y＝±x C． D．
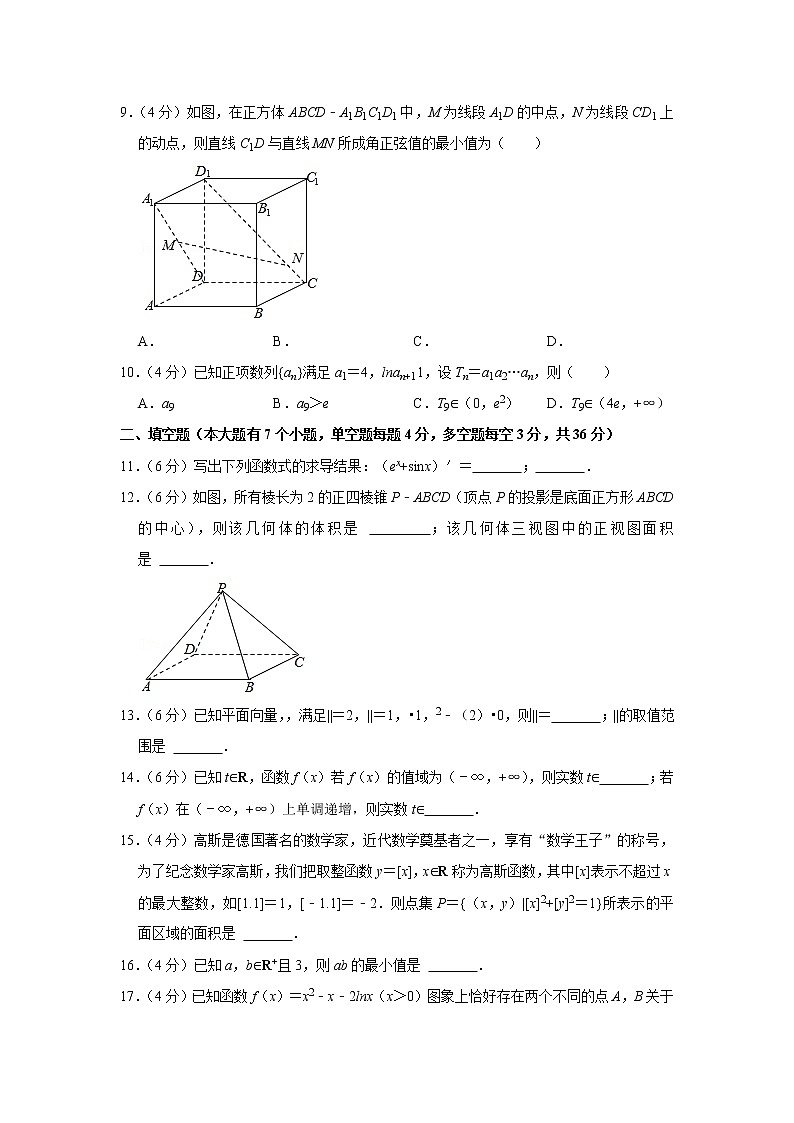
9．（4分）如图，在正方体ABCD﹣A1B1C1D1中，M为线段A1D的中点，N为线段CD1上的动点，则直线C1D与直线MN所成角正弦值的最小值为（　　）

A． B． C． D．
10．（4分）已知正项数列{an}满足a1＝4，lnan+11，设Tn＝a1a2…an，则（　　）
A．a9 B．a9＞e C．T9∈（0，e2） D．T9∈（4e，+∞）
二、填空题（本大题有7个小题，单空题每题4分，多空题每空3分，共36分）
11．（6分）写出下列函数式的求导结果：（ex+sinx）′＝　 　；　 　．
12．（6分）如图，所有棱长为2的正四棱锥P﹣ABCD（顶点P的投影是底面正方形ABCD的中心），则该几何体的体积是 　 　；该几何体三视图中的正视图面积是 　 　．

13．（6分）已知平面向量，，满足||＝2，||＝1，•1，2﹣（2）•0，则||＝　 　；||的取值范围是 　 　．
14．（6分）已知t∈R，函数f（x）若f（x）的值域为（﹣∞，+∞），则实数t∈　 　；若f（x）在（﹣∞，+∞）上单调递增，则实数t∈　 　．
15．（4分）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，为了纪念数学家高斯，我们把取整函数y＝[x]，x∈R称为高斯函数，其中[x]表示不超过x的最大整数，如[1.1]＝1，[﹣1.1]＝﹣2．则点集P＝{（x，y）|[x]2+[y]2＝1}所表示的平面区域的面积是 　 　．
16．（4分）已知a，b∈R+且3，则ab的最小值是 　 　．
17．（4分）已知函数f（x）＝x2﹣x﹣2lnx（x＞0）图象上恰好存在两个不同的点A，B关于y轴对称后在函数g（x）＝x2+bx﹣1（x＜0）的图象上，则实数b的取值范围是 　 　．
三、解答题（本大题有5个小题，共74分，解答应写出文字说明、证明过程或演算步骤）
18．（14分）已知函数f（x）＝2sinx•cos（x）．
（1）求的值；
（2）在△ABC中，f（A），b＝c＝2，求△ABC的面积．
19．（15分）已知数列{an}的前n项和Sn＝n2+λn（λ∈R），且a3＝6，正项等比数列{bn}满足b1＝a1，b2+b3＝a2+a4．
（1）求数列{an}和{bn}的通项公式；
（2）若cn＝|bn﹣2021|，求数列{cn}的前n项和Tn．
20．（15分）如图，四棱锥E﹣ABCD中，AE⊥AB，AC⊥BC，BA＝2AC，AC＝AE＝AD＝CD，M为CD中点．
（1）求证：AB⊥EM；
（2）若二面角E﹣AB﹣D的余弦值为，求直线DE与平面ABE所成角的正弦值．

21．（15分）如图，椭圆C：1（a＞b＞0）的离心率是，短轴长为2，且椭圆C与抛物线E：y2＝2px（p＞0）有一个相同的焦点F．A1，A2是椭圆的左、右顶点，F为椭圆的右焦点．过F的直线l与椭圆相交于A，B两点，与抛物线E相交于P，Q两点，点M为PQ的中点．
（1）求椭圆C和抛物线E的方程；
（2）记△ABA1的面积为S1，△MA2Q的面积为S2，若S1≥3S2，求直线l在y轴上截距的范围．

22．（15分）已知函数f（x）＝ln（x+a）+alnx，a∈R．
（1）求函数y＝f（x）的单调区间；
（2）当a＞0时，证明：ex﹣f（x）≥2．

2020-2021学年浙江省绍兴市诸暨市高二（下）期末数学试卷
参考答案与试题解析
一、选择题（每小题4分，共40分）
1．（4分）已知集合A，则A∩B＝（　　）
A． B． C． D．
【解答】解：∵B＝{x|﹣2＜x＜2}，
∴．
故选：D．
2．（4分）已知i为虚数单位，复数z＝i3•（1+i），则|z|＝（　　）
A．1 B． C．2 D．
【解答】解：z＝i3•（1+i）＝z＝﹣1•（1+i）＝﹣1﹣i，
故|z|＝|﹣1﹣i|．
故选：B．
3．（4分）已知空间直角坐标系中，O为坐标原点，P的坐标为（1，2，3），则（　　）
A．P到原点O的距离是 B．P到平面xOy的距离是1
C．P到平面xOy的距离是2 D．P到平面xOy的距离是3
【解答】解：由题可知，，
由P的坐标为（1，2，3），可知P到平面xOy的距离是3，
故选：D．
4．（4分）以直线ax﹣y﹣3﹣a＝0（a∈R）经过的定点为圆心，2为半径的圆的方程是（　　）
A．x2+y2﹣2x+6y+6＝0 B．x2+y2+2x﹣6y+6＝0
C．x2+y2+6x﹣2y+6＝0 D．x2+y2﹣6x+2y+6＝0
【解答】解：由题可知，直线过定点（1，﹣3），所以圆方程为（x﹣1）2+（y+3）2＝4，
即x2+y2﹣2x+6y+6＝0．
故选：A．
5．（4分）已知a，b∈R+，则“lna•lnb＞0”是“（a﹣1）•（b﹣1）＞0”的（　　）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
【解答】解：由题，因为a，b∈R+，所以lna⋅lnb＞0等价于（a﹣1）（b﹣1）＞0，即lna•lnb＞0”是“（a﹣1）•（b﹣1）＞0”的充分必要条件，
故选：C．
6．（4分）将函数的图象向右平移φ个单位与函数g（x）＝cos2x的图像重合，则φ可以是（　　）
A． B． C． D．
【解答】解析：由题可知，，
∵，
∴，
∴，当k＝﹣1时，，
故选：B．
7．（4分）若函数f（x）＝x2（x﹣a）（x﹣2）在x＝0处取得极大值，则实数a的取值范围是（　　）
A．（﹣∞，0） B．（0，+∞） C．（0，2） D．（2，+∞）
【解答】解：利用奇穿偶回法画图可知，
a＜0时，

结合图像，当a＜0时，在x＝0处取得极大值，
当0＜a＜2时，

当a＞2时，x＝a和x＝2交换位置即可，
结合图像，当a＞0时，在x＝0处取得极小值，
故选：A．
8．（4分）已知F1，F2为双曲线1（a＞0，b＞0）的左、右焦点，过F1作yx的垂线分别交双曲线的左、右两支于B，C两点（如图）．若∠CBF2＝∠CF2B，则双曲线的渐近线方程为（　　）

A．y＝±x B．y＝±x C． D．
【解答】解：由∠CBF2＝∠CF2B可设|BC|＝|CF2|＝m，由|CF1|﹣|CF2|＝2a得，|BF1|＝2a，所以|BF2|＝4a，，
又得，
∴，令a＝1，化简得：b2﹣2b﹣2＝0，得，
所以渐近线方程为，
故选：C．
9．（4分）如图，在正方体ABCD﹣A1B1C1D1中，M为线段A1D的中点，N为线段CD1上的动点，则直线C1D与直线MN所成角正弦值的最小值为（　　）

A． B． C． D．
【解答】解：以D为原点建立平面直角坐标系，设正方体棱长为2，
则M（1，0，1），C（0，2，0），D1（0，0，2），则，
因为N为线段CD1上的动点，
所以不妨设，则得N（0，﹣2λ+2，2λ），
所以，
则cos，||
＝|||，
因为λ∈[0，1]，所以8（λ）²∈[，6]，
所以cos，，所以sin，，
所以直线C1D与直线MN所成角正弦值的最小值为．
故选：C．

10．（4分）已知正项数列{an}满足a1＝4，lnan+11，设Tn＝a1a2…an，则（　　）
A．a9 B．a9＞e C．T9∈（0，e2） D．T9∈（4e，+∞）
【解答】解：由x﹣1≥lnx，得，
所以，
故，
即lnT9＞（2）ln4，
⇒T944e，
∴T9＜e2不正确，
lna9ln4，
∴a9，而1e，
∴ABC都不正确，
故选：D．
二、填空题（本大题有7个小题，单空题每题4分，多空题每空3分，共36分）
11．（6分）写出下列函数式的求导结果：（ex+sinx）′＝　ex+cosx　；　　．
【解答】解：（ex+sinx）'＝ex+cosx；
．
故答案为：ex+cosx；．
12．（6分）如图，所有棱长为2的正四棱锥P﹣ABCD（顶点P的投影是底面正方形ABCD的中心），则该几何体的体积是 　　；该几何体三视图中的正视图面积是 　　．

【解答】解：设底面正方形ABCD外接圆半径为r，则2r＝AC，∴，
设锥高为h，则h2+r2＝PA2，解得，所以；
该几何体三视图的正视图面积是．
13．（6分）已知平面向量，，满足||＝2，||＝1，•1，2﹣（2）•0，则||＝　　；||的取值范围是 　　．
【解答】解：设，∵||＝2，||＝1，∴•2cosθ＝﹣1，∴，∴，
∴||；
如图建立平面直角坐标系，则，，设，
∵2﹣（2）•0，
∴，即，
则C是以M（）为圆心，以为半径的圆上的点，
∴，即点A，C间的距离，由，
圆的半径为，∴，
则，
故答案为：．

14．（6分）已知t∈R，函数f（x）若f（x）的值域为（﹣∞，+∞），则实数t∈　[0，1]　；若f（x）在（﹣∞，+∞）上单调递增，则实数t∈　{0}∪[1，+∞）　．
【解答】解：根据题意，函数f（x），
对于第一空：若f（x）的值域为（﹣∞，+∞），则有t2≤t，
解可得0≤t≤1，即t的取值范围为[0，1]；
对于第二空：若f（x）在（﹣∞，+∞）上单调递增，则有，
解可得t＝0或t≥1，即t的取值范围为{0}∪[1，+∞）；
故答案为：[0，1]，{0}∪[1，+∞）．
15．（4分）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，为了纪念数学家高斯，我们把取整函数y＝[x]，x∈R称为高斯函数，其中[x]表示不超过x的最大整数，如[1.1]＝1，[﹣1.1]＝﹣2．则点集P＝{（x，y）|[x]2+[y]2＝1}所表示的平面区域的面积是 　4　．
【解答】解：把[x]2+[y]2＝1看成或或或四个平面区域组成，
即或或或，
作出平面区域如图所示，
平面区域是甴四个边长为 1 的正方形组成，总面积为 1×4＝4，
故答案为：4．

16．（4分）已知a，b∈R+且3，则ab的最小值是 　1　．
【解答】解：∵0，∴
∴3，
∴a2+ab+b2≥3ab≥3，∴ab≥1，当且仅当“a＝b＝1”时等号成立．
故答案为：1．
17．（4分）已知函数f（x）＝x2﹣x﹣2lnx（x＞0）图象上恰好存在两个不同的点A，B关于y轴对称后在函数g（x）＝x2+bx﹣1（x＜0）的图象上，则实数b的取值范围是 　（1，）　．
【解答】解：g（x）关于y轴对称的函数为h（x）＝g（﹣x）＝x2﹣bx﹣1，
条件等价于h（x）与f（x）的图象有两个交点，
即方程f（x）＝h（x）有两个不同的根．
即x2﹣x﹣2lnx＝x2﹣bx﹣1，整理得；
设，则，
所以G（x）在上递增，在上递减，
最大值为，
又当时，，
所以b的取值范围为（1，）．
故答案为：（1，）．
三、解答题（本大题有5个小题，共74分，解答应写出文字说明、证明过程或演算步骤）
18．（14分）已知函数f（x）＝2sinx•cos（x）．
（1）求的值；
（2）在△ABC中，f（A），b＝c＝2，求△ABC的面积．
【解答】解：（1），
所以．
（2）由，得或，
解得，或，因此，或；
所以，或者．
19．（15分）已知数列{an}的前n项和Sn＝n2+λn（λ∈R），且a3＝6，正项等比数列{bn}满足b1＝a1，b2+b3＝a2+a4．
（1）求数列{an}和{bn}的通项公式；
（2）若cn＝|bn﹣2021|，求数列{cn}的前n项和Tn．
【解答】（1）当n≥2时，，
由a3＝6，
得λ＝1，
即，
当n＝1时，a1＝S1＝2，
当n≥2时，an＝2n，
所以an＝2n；
设正项等比数列{bn}的公比为q（q＞0），
则，
所以q2+q﹣6＝0，
解得q＝2或q＝﹣3（舍）；
所以．
（2）当n≤10时，，
当n≥11时，，
即．
20．（15分）如图，四棱锥E﹣ABCD中，AE⊥AB，AC⊥BC，BA＝2AC，AC＝AE＝AD＝CD，M为CD中点．
（1）求证：AB⊥EM；
（2）若二面角E﹣AB﹣D的余弦值为，求直线DE与平面ABE所成角的正弦值．

【解答】（1）证明：线面垂直，∵BA＝2AC，AC⊥BC，∴，
又AC＝AD＝CD，M为CD中点，则有，
∴AB∥CD，CD⊥AM，CD⊥AE，AM∩AE＝A，∴CD⊥平面AME，
∴AB⊥平面AME，所以AB⊥EM．

（2）．法一：由（1）知：AB⊥平面AME，∴∠EAM即为二面角E﹣AB﹣D的平面角，设为θ，
过点M作MH⊥EA于H，记AC＝AD＝CD＝1，∴Rt△MAH中：，
又∵CD∥面AEB，∴D到面AEB的距离与M到面AEB的距离相等，
二面角E﹣AB﹣D的平面角设为θ，
∴，
法二：以A为原点，AB，AM为x轴，y轴，垂直平面ABCD向上方向为z轴，
如图建立空间直角坐标系，令AC＝2，则；
因为二面角E﹣AB﹣D的余弦值为，设EH⊥AM，则；
所以，则；又，
设平面ABE的法向量为，取，则，所以，
令直线DE与平面ABE所成角为θ，
则．

21．（15分）如图，椭圆C：1（a＞b＞0）的离心率是，短轴长为2，且椭圆C与抛物线E：y2＝2px（p＞0）有一个相同的焦点F．A1，A2是椭圆的左、右顶点，F为椭圆的右焦点．过F的直线l与椭圆相交于A，B两点，与抛物线E相交于P，Q两点，点M为PQ的中点．
（1）求椭圆C和抛物线E的方程；
（2）记△ABA1的面积为S1，△MA2Q的面积为S2，若S1≥3S2，求直线l在y轴上截距的范围．

【解答】解：（1）根据题意解得，抛物线焦点F（1，0），
因此椭圆，抛物线E：y2＝4x．
（2）设l：x＝ty+1，A（x1，y1），B（x2，y2），P（x3，y3），Q（x4，y4），联立l与椭圆，
整理得：（3t2+4）y2+6ty﹣9＝0，判别式：Δ＝（6t）2﹣4（3t2+4）（﹣9）＝144（t2+1），
弦长公式：，
联立l与抛物线，整理得：y2﹣4ty﹣4＝0，判别式：Δ＝（﹣4t）2﹣4（﹣4）＝16（t2+1），
弦长公式：，
因为S1≥3S2，因此，解得：，
在y轴上截距或，因此在y轴上截距取值范围是．
22．（15分）已知函数f（x）＝ln（x+a）+alnx，a∈R．
（1）求函数y＝f（x）的单调区间；
（2）当a＞0时，证明：ex﹣f（x）≥2．
【解答】解：（1）①当a≥0时，f（x）的定义域为恒成立，
故f（x）在（0，+∞）上单调递增；
②当﹣1≤a＜0时，f（x）的定义域为在（﹣a，+∞）上恒成立，
故f（x）在（﹣a，+∞）上单调递增；
③当a＜﹣1时，f（x）的定义域为，
当时f'（x）＞0，f（x）单调递增，
当时f'（x）＜0，f（x）单调递减；
综上，当a≥0时，f（x）在（0，+∞）上单调递增；
当﹣1≤a＜0时，f（x）在（﹣a，+∞）上单调递增；
当a＜﹣1时，f（x）在单调递增，在单调递减．
（2）证明：①首先证明引理1：lnx≤x﹣1，
令，故lnx≤x﹣1得证；
②接着证明引理2：；
令，
故q（x）在[0，+∞）上单调递增，故q（x）≥q（0）＝0在[0，+∞）上恒成立，
故．
③现在证明当a＞0时，；
此时，f（x）的定义域为（0，+∞），
由故由引理1和引理2可得ex﹣f（x）x2+x+1﹣（x+a﹣1）﹣a（x﹣1）x2﹣ax+2，
而x2﹣ax+2≥2⇔x2﹣ax0，（x﹣a）2≥0，恒成立，
故，证毕．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/5/27 10:14:28；用户：高中数学；邮箱：sdgs@xyh.com；学号：28144983