

【解析版】2022年河北省廊坊市七年级下期末数学试卷
展开
2022学年河北省廊坊市七年级(下)期末数学试卷
一、选择题(本大题共16个小题,1-6小题,每小题2分;7-16小题,每小题2分;共42分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.平面直角坐标系中,点(1,﹣2)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.9的平方根是( )
A. 3 B. ﹣3 C. ±3 D. 81
3.下列四个实数中,是无理数的是( )
A. B. 0 C. D.
4.方程kx+3y=5有一组解是,则k的值是( )
A. 1 B. ﹣1 C. 0 D. 2
5.下列调査中,适合采用全面调査(普査)方式的是( )
A. 调査某池塘中现有鱼的数量
B. 对端午节期间市场上粽子质量情况的调査
C. 企业招聘,对应聘人员进行面试
D. 对某类烟花爆竹燃放安全情况的调査
6.如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
A. 140° B. 60° C. 50° D. 40°
7.下列说法正确的是( )
A. 相等的角是对顶角
B. 在同一平面内,若a丄b,b丄c,则a∥c
C. 内错角相等
D. 过一点有且只有一条直线与已知直线平行
8.一个正方形的面积是12,估计它的边长大小在( )
A. 2与3之间 B. 3与4之间 C. 4与5之间 D. 5与6之间
9.如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到CD,若点C的坐标为(6,3),则点D的坐标为( )
A. (2,6) B. (2,5) C. (6,2) D. (3,6)
10.下列条件不能判定AB∥CD的是( )
A. ∠3=∠4 B. ∠A+∠ADC=180° C. ∠1=∠2 D. ∠A=∠5
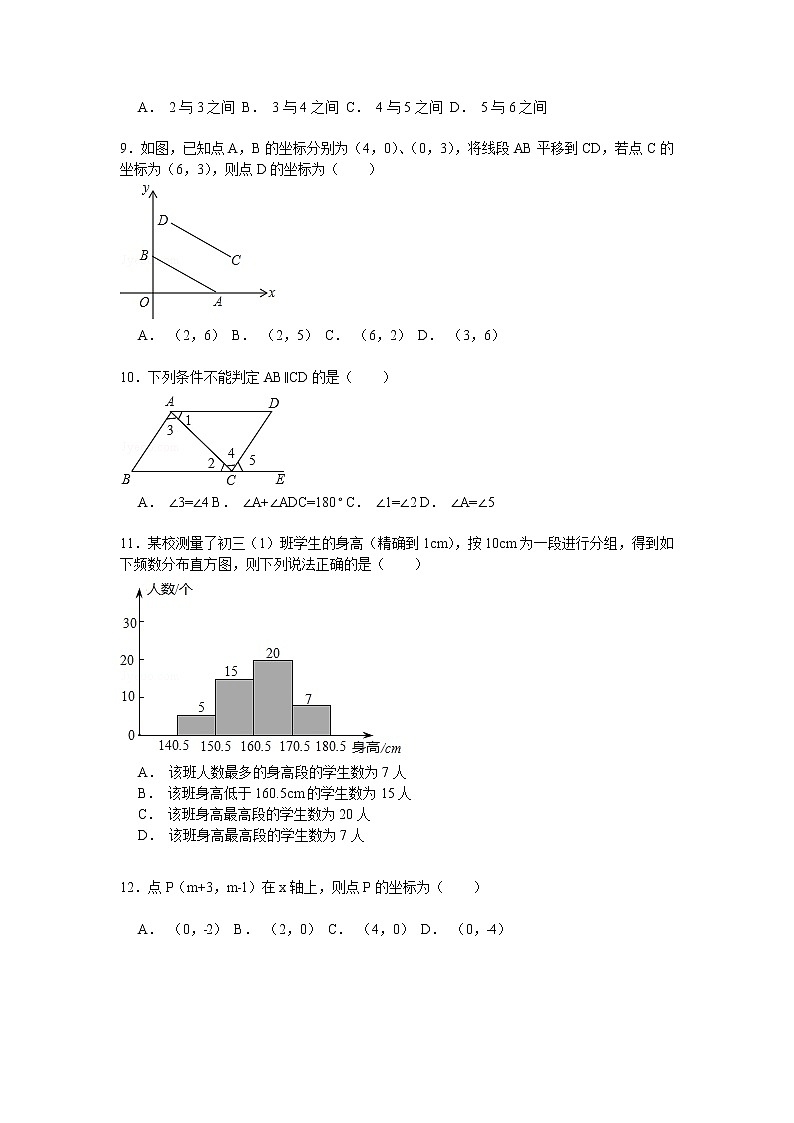
11.某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如下频数分布直方图,则下列说法正确的是( )
A. 该班人数最多的身高段的学生数为7人
B. 该班身高低于160.5cm的学生数为15人
C. 该班身高最高段的学生数为20人
D. 该班身高最高段的学生数为7人
12.点P(m+3,m﹣1)在x轴上,则点P的坐标为( )
A. (0,﹣2) B. (2,0) C. (4,0) D. (0,﹣4)
13.如图,在数轴上表示﹣1,﹣的对应点为A,B,若点A是线段BC的中点,则点C表示的数为( )
A. 1﹣ B. 2﹣ C. ﹣1 D. ﹣2
14.已知是二元一次方程组的解,则2m﹣n的算术平方根为( )
A. ±2 B. C. 2 D. 4
15.若关于x的不等式组无解,则实数a的取值范围是( )
A. a<﹣4 B. a=﹣4 C. a>﹣4 D. a≥﹣4
16.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A. ∠A+∠C+∠D+∠E=360° B. ∠A+∠D=∠C+∠E
C. ∠A﹣∠C+∠D+∠E=180° D. ∠E﹣∠C+∠D﹣∠A=90°
二、填空题(本大题共4个小题,每小题3分,共12分,把答案写在题横线上)
17.x与1的差不大于3.用不等式表示为 .
18.数学活动中.张明和王丽向老师说明他们的位置(单位:m).
张明:我这里的坐标是(﹣200,300);
王丽:我这里的坐标是(300,300).
则老师知道张明与王丽之间的距离是 m.
19.小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是 度.
20.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A3的坐标为 ,点A2015的坐标为 .
三、解答题(本大题共6个小题,总计66分,解答应写出文字说明、证明过程或演算步骤)
21.(1)计算:|1﹣|+×﹣
(2)解方程组:
(3)解不等式组并把它的解集表示在如图数轴上.
22.列方程或方程组解决问题:
某学校计划购进一批电脑和电子白板,经过市场调研得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.求每台电脑、每台电子白板各多少万元?
23.如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(Ⅰ)建立以点B为原点,AB边所在直线为x轴的直角坐标系.写出点A、B、C、D的坐标;
(Ⅱ)求出四边形ABCD的面积;
(Ⅲ)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形A′B′C′D′.
24.某中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调整兴趣活动小组,为此进行了一次抽样调查,根据采集到的数据绘制的统计图(不完整)如下:
请你根据图中提供的信息,完成下列问题:
(1)图1中,“电脑”部分所对应的圆心角为 度;
(2)共抽查了 名学生;
(3)在图2中,将“体育”部分的图形补充完整;
(4)爱好“书画”的人数占被调查人数的百分比 ;
(5)估计现有学生中,有 人爱好“书画”.
25.完成下面的证明:
(1)如图1,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
证明:∵DE∥BA,
∴∠FDE= ( ),
∵DF∥CA,
∴∠A= ( ),
∴∠FDE=∠A;
(2)如图2,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD,求证:AC∥BD;
证明:∵∠C=∠COA,∠D=∠BOD,
∵∠COA=∠BOD( ),
∴∠C= ,
∴AC∥BD( ).
26.如图,已知:∠1=∠2,∠D=50°,求∠B的度数.
27.为了更好治理流溪河水质,保护环境,市治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 B型
价格(万元/台) a b
处理污水量(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值.
(2)经预算:市治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案.
(3)在(2)问的条件下,若每月要求处理流溪河两岸的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
2022学年河北省廊坊市七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共16个小题,1-6小题,每小题2分;7-16小题,每小题2分;共42分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.平面直角坐标系中,点(1,﹣2)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
考点: 点的坐标.
分析: 根据各象限内点的坐标特征解答.
解答: 解:点(1,﹣2)在第四象限.
故选D.
点评: 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
2.9的平方根是( )
A. 3 B. ﹣3 C. ±3 D. 81
考点: 平方根.
分析: 如果一个非负数x的平方等于a,那么x是a是算术平方根,根据此定义解题即可解决问题.
解答: 解:∵(±3)2=9,
∴9的平方根是±3.
故选:C.
点评: 本题主要考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
3.下列四个实数中,是无理数的是( )
A. B. 0 C. D.
考点: 无理数.
分析: 根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,找出无理数.
解答: 解:=2,是有理数,0,是有理数,
∴只有为无理数.
故选C.
点评: 本题考查了无理数的知识,解答本题的关键是熟练掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.
4.方程kx+3y=5有一组解是,则k的值是( )
A. 1 B. ﹣1 C. 0 D. 2
考点: 二元一次方程的解.
分析: 知道了方程的解,可以把这组解代入方程,得到一个含有未知数k的一元一次方程,从而可以求出k的值.
解答: 解:把是代入方程kx+3y=5中,得
2k+3=5,
解得k=1.
故选A.
点评: 本题考查了二元一次方程的解,解题关键是把方程的解代入原方程,使原方程转化为以系数k为未知数的方程.
5.下列调査中,适合采用全面调査(普査)方式的是( )
A. 调査某池塘中现有鱼的数量
B. 对端午节期间市场上粽子质量情况的调査
C. 企业招聘,对应聘人员进行面试
D. 对某类烟花爆竹燃放安全情况的调査
考点: 全面调查与抽样调查.
分析: 由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
解答: 解:A、调査某池塘中现有鱼的数量,用抽样调查,故错误;
B、对端午节期间市场上粽子质量情况的调査,用抽样调查,故错误;
C、企业招聘,对应聘人员进行面试,用普查方式,正确;
D、对某类烟花爆竹燃放安全情况的调査,用抽样调查,故错误;
故选:C.
点评: 本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
6.如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
A. 140° B. 60° C. 50° D. 40°
考点: 平行线的性质.
分析: 延长CD,先根据补角的定义得出∠EFD的度数,再由平行线的性质即可得出结论.
解答: 解:延长CD,
∵∠CDE=140°,
∴∠EDF=40°.
∵AB∥CD,
∴∠A=∠EDF=40°.
故选D.
点评: 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
7.下列说法正确的是( )
A. 相等的角是对顶角
B. 在同一平面内,若a丄b,b丄c,则a∥c
C. 内错角相等
D. 过一点有且只有一条直线与已知直线平行
考点: 命题与定理.
分析: 根据对顶角的两边互为反向延长线,平行线的性质,对各选项分析判断后利用排除法求解.
解答: 解:A、相等的角的两边不一定互为反向延长线,故本选项错误;
B、正确;
C、两直线平行,内错角相等,故本选项错误;
D,过直线外一点有且只有一条直线与已知直线平行,故本选项错误;
故选:B.
点评: 本题考查了对顶角,平行线的性质,解决本题的关键是熟记对顶角,平行线的性质.
8.一个正方形的面积是12,估计它的边长大小在( )
A. 2与3之间 B. 3与4之间 C. 4与5之间 D. 5与6之间
考点: 估算无理数的大小;算术平方根.
分析: 先根据正方形的面积是12计算出其边长,再估算出该数的大小即可.
解答: 解:∵一个正方形的面积是12,
∴该正方形的边长为,
∵9<12<16,
∴3<<4.
故选B.
点评: 本题考查的是估算无理数的大小及正方形的性质,根据题意估算出的取值范围是解答此题的关键.
9.如图,已知点A,B的坐标分别为(4,0)、(0,3),将线段AB平移到CD,若点C的坐标为(6,3),则点D的坐标为( )
A. (2,6) B. (2,5) C. (6,2) D. (3,6)
考点: 坐标与图形变化-平移.
分析: 先根据A、C两点确定出平移规律,再根据此规律解答.
解答: 解:∵A(4,0)、C(6,3)是对应点,
∴平移规律为向右平移2个单位,向上平移3个单位,
∴0+2=2,3+3=6,
∴点D的坐标为(2,6).
故选A.
点评: 本题考查了坐标与图形的变化﹣平移,结合图形根据点A、C的坐标确定出平移规律是解题的关键.
10.下列条件不能判定AB∥CD的是( )
A. ∠3=∠4 B. ∠A+∠ADC=180° C. ∠1=∠2 D. ∠A=∠5
考点: 平行线的判定.
分析: 根据平行线的判定方法对各选项分析判断后利用排除法求解.
解答: 解:A、∵∠3=∠4,∴AB∥CD(内错角相等,两直线平行),故本选项错误;
B、∵∠A+∠ADC=180°,∴AB∥CD(同旁内角互补,两直线平行),故本选项错误.
C、∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行),判定的不是AB∥CD,故本选项正确;
D、∵∠B=∠5,∴AB∥CD(同位角相等,两直线平行),故本选项错误;
故选C.
点评: 本题考查了平行线的判定,熟练掌握平行线的判定方法是解题的关键,要注意内错角、同位角、同旁内角与截线、被截线的关系.
11.某校测量了初三(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如下频数分布直方图,则下列说法正确的是( )
A. 该班人数最多的身高段的学生数为7人
B. 该班身高低于160.5cm的学生数为15人
C. 该班身高最高段的学生数为20人
D. 该班身高最高段的学生数为7人
考点: 频数(率)分布直方图.
专题: 图表型.
分析: 根据频数直方图的意义,表示每段中的人数,即可得到答案.
解答: 解:由频数直方图可以看出:该班人数最多的身高段的学生数为20人;该班身高低于160.5cm的学生数为20人;该班身高最高段的学生数为7人;
故选D.
点评: 考查获取信息(读图)进行判断的能力.
12.点P(m+3,m﹣1)在x轴上,则点P的坐标为( )
A. (0,﹣2) B. (2,0) C. (4,0) D. (0,﹣4)
考点: 点的坐标.
分析: 根据x轴上点的纵坐标为0列方程求出m的值,再求出横坐标即可得解.
解答: 解:∵点P(m+3,m﹣1)在x轴上,
∴m﹣1=0,
解得m=1,
∴m+3=1+3=4,
∴点P的坐标为(4,0).
故选C.
点评: 本题考查了点的坐标,熟记x轴上点的纵坐标为0是解题的关键.
13.如图,在数轴上表示﹣1,﹣的对应点为A,B,若点A是线段BC的中点,则点C表示的数为( )
A. 1﹣ B. 2﹣ C. ﹣1 D. ﹣2
考点: 实数与数轴.
分析: 设C表示的数是x,根据A是线段BC的中点,列出算式,求出x的值即可.
解答: 解:设C表示的数是x,
∵A=﹣1,B=﹣,
∴=﹣1,
∴x=﹣2.
故选D.
点评: 本题考查了实数与数轴、线段的中点.解题的关键是理解线段中点的含义.
14.已知是二元一次方程组的解,则2m﹣n的算术平方根为( )
A. ±2 B. C. 2 D. 4
考点: 二元一次方程组的解;算术平方根.
分析: 由是二元一次方程组的解,根据二元一次方程根的定义,可得,即可求得m与n的值,继而求得2m﹣n的算术平方根.
解答: 解:∵是二元一次方程组的解,
∴,
解得:,
∴2m﹣n=4,
∴2m﹣n的算术平方根为2.
故选C.
点评: 此题考查了二元一次方程组的解、二元一次方程组的解法以及算术平方根的定义.此题难度不大,注意理解方程组的解的定义.
15.若关于x的不等式组无解,则实数a的取值范围是( )
A. a<﹣4 B. a=﹣4 C. a>﹣4 D. a≥﹣4
考点: 解一元一次不等式组.
分析: 先求出①中x的取值范围,再根据不等式组无解确定a的取值范围即可.
解答: 解:解①移项得,2x﹣4x>7+1,
合并同类项得,﹣2x>8,
系数化为1得,x<﹣4,
故得,
由于此不等式组无解,故a≥﹣4.
故选D.
点评: 本题考查的是一元一次不等式组的解法,解答此题的关键是熟知解不等式组解集应遵循的原则“同大取较大,同小去较小,大小小大中间找,大大小小解不了”的原则.
16.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A. ∠A+∠C+∠D+∠E=360° B. ∠A+∠D=∠C+∠E
C. ∠A﹣∠C+∠D+∠E=180° D. ∠E﹣∠C+∠D﹣∠A=90°
考点: 平行线的性质.
分析: 过点C作CG∥AB,过点D作DH∥EF,根据两直线平行,内错角相等可得∠A=∠ACG,∠CDH=∠DCG,两直线平行,同旁内角互补可得∠EDH=180°﹣∠E,然后表示出∠C整理即可得解.
解答: 解:如图,过点C作CG∥AB,过点D作DH∥EF,
则∠A=∠ACG,∠EDH=180°﹣∠E,
∵AB∥EF,
∴CG∥DH,
∴∠CDH=∠DCG,
∴∠C=∠ACG+∠CDH=∠A+∠D﹣(180°﹣∠E),
∴∠A﹣∠C+∠D+∠E=180°.
故选C.
点评: 本题考查了平行线的性质,此类题目难点在于过拐点作平行线.
二、填空题(本大题共4个小题,每小题3分,共12分,把答案写在题横线上)
17.x与1的差不大于3.用不等式表示为 x﹣1≤3 .
考点: 由实际问题抽象出一元一次不等式.
分析: x与1的差即x﹣1,不大于即≤,据此列不等式.
解答: 解:由题意得,x﹣1≤3.
故答案为:x﹣1≤3.
点评: 本题考查了由实际问题抽象出一元一次不等式,读懂题意,抓住关键词语,弄清运算的先后顺序和不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.
18.数学活动中.张明和王丽向老师说明他们的位置(单位:m).
张明:我这里的坐标是(﹣200,300);
王丽:我这里的坐标是(300,300).
则老师知道张明与王丽之间的距离是 500 m.
考点: 坐标确定位置.
分析: 根据纵坐标相等,两人之间的距离等于横坐标的差解答.
解答: 解:∵张明的坐标是(﹣200,300),王丽的坐标是(300,300),
∴两人之间的距离为300﹣(﹣200)=300+200=500.
故答案为:500.
点评: 本题考查了坐标确定位置,观察出两人的纵坐标相等是解题的关键.
19.小亮将一个直角三角板和一把直尺(如图所示)叠放在一起,如果∠β=32°,那么∠α是 58 度.
考点: 平行线的性质.
分析: 延长AC交直尺于点E,根据对顶角相等可求出∠CDE=∠β=32°,再由直角三角形的性质求出∠DEC的度数,根据平行线的性质即可得出结论.
解答: 解:延长AC交直尺于点E,
∵∠β与∠CDE是对顶角,∠β=32°,
∴∠CDE=∠β=32°,
∴∠DEC=90°﹣32°=58°.
∵直尺的两边互相平行,
∴∠α=∠AED=58°.
故答案为:58.
点评: 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
20.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A3的坐标为 (﹣3,1) ,点A2015的坐标为 (﹣3,1) .
考点: 规律型:点的坐标.
专题: 新定义.
分析: 根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2015除以4,根据商和余数的情况确定点A2015的坐标即可.
解答: 解:∵点A1的坐标为(3,1),
∴A2(﹣1+1,3+1)即(0,4),A3(﹣3,﹣1+2)即(﹣3,1),A4(1﹣1,﹣3+1)即(0,﹣2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2015÷4=503余3,
∴点A2015的坐标与A3的坐标相同,为(﹣3,﹣1+2),即(﹣3,1);
故答案为:(﹣3,1);(﹣3,1).
点评: 此题考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.
三、解答题(本大题共6个小题,总计66分,解答应写出文字说明、证明过程或演算步骤)
21.(1)计算:|1﹣|+×﹣
(2)解方程组:
(3)解不等式组并把它的解集表示在如图数轴上.
考点: 实数的运算;解二元一次方程组;在数轴上表示不等式的解集;解一元一次不等式组.
分析: (1)根据实数的运算方法,首先计算开方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
(2)应用代入法解二元一次方程组,求出方程组的解是多少即可.
(3)首先根据解一元一次不等式组的方法,求出不等式组的解集是多少;然后把不等式组的解集表示在数轴上即可.
解答: 解:(1)|1﹣|+×﹣
=+()×
=
=﹣
(2)由②,可得:x=3y+18,
把x=3y+18代入①,可得
8(3y+18)+9y=12,
解得y=﹣4,
把y=﹣4代入x=3y+18,可得
x=3×(﹣4)+18=6,
∴方程组的解为:
.
(3)解不等式①,可得:x<2,
解不等式②,可得:x≥﹣1,
∴不等式组的解集是:﹣1≤x<2,
把它的解集表示在数轴上为:
.
点评: (1)此题主要考查了实数的四则混合运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了解一元一次不等式组的方法,以及在数轴上表示不等式的解集的方法,要熟练掌握.
(3)此题还考查了解二元一次方程组的方法,要熟练掌握两种常用的方法:代入法和消元法.
22.列方程或方程组解决问题:
某学校计划购进一批电脑和电子白板,经过市场调研得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.求每台电脑、每台电子白板各多少万元?
考点: 二元一次方程组的应用.
分析: 设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元,列方程组求解.
解答: 解:设每台电脑x万元,每台电子白板y万元,
由题意得,,
解得:.
答:每台电脑0.5万元,每台电子白板1.5万元.
点评: 本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.
23.如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(Ⅰ)建立以点B为原点,AB边所在直线为x轴的直角坐标系.写出点A、B、C、D的坐标;
(Ⅱ)求出四边形ABCD的面积;
(Ⅲ)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形A′B′C′D′.
考点: 作图-平移变换.
分析: (1)根据题意首先建立平面直角坐标系,进而得出各点坐标;
(2)利用S四边形ABCD=S△ABD+S△CBD进而求出即可;
(3)利用平移的性质得出平移后对应点坐标,即可得出答案.
解答: 解:(1)如图所示:A(﹣4,0)、B(0,0)、C2,2)、D(0,3);
(2)∵S△DCB=×3×2=3,S△ABD=×3×4=6,
∴S四边形ABCD=S△ABD+S△CBD=9;
(3)如图所示:四边形A′B′C′D′即为所求.
点评: 此题主要考查了图形的平移以及四边形面积求法等知识,得出对应点坐标是解题关键.
24.某中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调整兴趣活动小组,为此进行了一次抽样调查,根据采集到的数据绘制的统计图(不完整)如下:
请你根据图中提供的信息,完成下列问题:
(1)图1中,“电脑”部分所对应的圆心角为 126 度;
(2)共抽查了 80 名学生;
(3)在图2中,将“体育”部分的图形补充完整;
(4)爱好“书画”的人数占被调查人数的百分比 10% ;
(5)估计现有学生中,有 287 人爱好“书画”.
考点: 条形统计图;用样本估计总体;扇形统计图.
专题: 计算题.
分析: (1)由“电脑”部分的百分比乘以360即可得到结果;
(2)由“电脑”部分的人数除以占的百分比即可求出调查的学生总数;
(3)由总学生数减去其他的人数求出“体育”部分的人数,补全统计图即可;
(4)由“书画”部分的学生数除以总人数即可得到结果;
(5)由求出“书画”部分的百分比乘以2870即可得到结果.
解答: 解:(1)根据题意得:360°×35%=126°;
(2)根据题意得:28÷35%=80(人);
(3)“体育“部分的是80﹣(28+24+8)=20人,补全统计图,
如图所示:
(4)根据题意得:8÷80=10%;
(5)根据题意得:2870×10%=287(人).
故答案为:(1)126;(2)80;(4)10%;(5)287.
点评: 此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.
25.完成下面的证明:
(1)如图1,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
证明:∵DE∥BA,
∴∠FDE= ∠BFD ( 两直线平行,内错角相等 ),
∵DF∥CA,
∴∠A= ∠BFD ( 两直线平行,同位角相等 ),
∴∠FDE=∠A;
(2)如图2,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD,求证:AC∥BD;
证明:∵∠C=∠COA,∠D=∠BOD,
∵∠COA=∠BOD( 对顶角相等 ),
∴∠C= ∠D ,
∴AC∥BD( 内错角相等,两直线平行 ).
考点: 平行线的判定与性质.
专题: 推理填空题.
分析: (1)根据平行线的性质得出∠FDE=∠BFD,∠A=∠BFD,推出即可;
(2)根据对顶角相等和已知求出∠C=∠D,根据平行线的判定推出即可.
解答: (1)证明:∵DE∥BA,
∴∠FDE=∠BFD(两直线平行,内错角相等),
∵DF∥CA,
∴∠A=∠BFD(两直线平行,同位角相等),
∴∠FDE=∠A,
故答案为:∠BFD,两直线平行,内错角相等,∠BFD,两直线平行,同位角相等;
(2)证明:∵∠C=∠COA,∠D=∠BOD,
又∵∠COA=∠BOD(对顶角相等),
∴∠C=∠D,
∴AC∥BD(内错角相等,两直线平行),
故答案为:对顶角相等,∠D,内错角相等,两直线平行.
点评: 本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.
26.如图,已知:∠1=∠2,∠D=50°,求∠B的度数.
考点: 平行线的判定与性质.
专题: 计算题.
分析: 此题首先要根据对顶角相等,结合已知条件,得到一组同位角相等,再根据平行线的判定得两条直线平行.然后根据平行线的性质得到同旁内角互补,从而进行求解.
解答: 解:∵∠1=∠2,∠2=∠EHD,
∴∠1=∠EHD,
∴AB∥CD;
∴∠B+∠D=180°,
∵∠D=50°,
∴∠B=180°﹣50°=130°.
点评: 综合运用了平行线的性质和判定,难度不大.
27.为了更好治理流溪河水质,保护环境,市治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 B型
价格(万元/台) a b
处理污水量(吨/月) 240 200
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值.
(2)经预算:市治污公司购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案.
(3)在(2)问的条件下,若每月要求处理流溪河两岸的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
考点: 一元一次不等式的应用;二元一次方程组的应用.
专题: 应用题.
分析: (1)根据“购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元”即可列出方程组,继而进行求解;
(2)可设购买污水处理设备A型设备x台,B型设备(10﹣x)台,则有12x+10(10﹣x)≤105,解之确定x的值,即可确定方案;
(3)因为每月要求处理流溪河两岸的污水量不低于2040吨,所以有240x+200(10﹣x)≥2040,解之即可由x的值确定方案,然后进行比较,作出选择.
解答: 解:(1)根据题意得:,
∴;
(2)设购买污水处理设备A型设备x台,B型设备(10﹣x)台,
则:12x+10(10﹣x)≤105,
∴x≤2.5,
∵x取非负整数,
∴x=0,1,2,
∴有三种购买方案:
①A型设备0台,B型设备10台;
②A型设备1台,B型设备9台;
③A型设备2台,B型设备8台.
(3)由题意:240x+200(10﹣x)≥2040,
∴x≥1,
又∵x≤2.5,x取非负整数,
∴x为1,2.
当x=1时,购买资金为:12×1+10×9=102(万元),
当x=2时,购买资金为:12×2+10×8=104(万元),
∴为了节约资金,应选购A型设备1台,B型设备9台.
点评: 本题考查一元一次不等式及二元一次方程组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系,同时要注意分类讨论思想的运用.
2023-2024学年河北省廊坊市固安县七年级(上)期末数学试卷(含解析): 这是一份2023-2024学年河北省廊坊市固安县七年级(上)期末数学试卷(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河北省廊坊市广阳区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年河北省廊坊市广阳区七年级(下)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河北省廊坊市广阳区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年河北省廊坊市广阳区七年级(下)期末数学试卷(含解析),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












