2022年宁夏中考数学考前模拟冲刺试题(word版含答案)

这是一份2022年宁夏中考数学考前模拟冲刺试题(word版含答案)，共22页。试卷主要包含了下列各数比﹣2小的是，下列几何体中，俯视图是矩形的是，分解因式等内容，欢迎下载使用。

2022年宁夏中考数学考前模拟冲刺试题
一．选择题（共8小题，满分24分，每小题3分，在每小题给出的四个选项中只有一个是符合题目要求的）
1．下列各数比﹣2小的是（　　）
A．0 B．﹣3 C．3 D．﹣
2．下列几何体中，俯视图是矩形的是（　　）
A． B． C． D．
3．太原古县城的打造历时8年，耗资将近300亿元，是太原境内的一个重点工程，它是一个在明代早期修建的古城，很好的传承了“晋阳古城”的文脉，并延续了“晋阳古城”的历史文化．数据300亿元用科学记数法表示为（　　）
A．3×102元 B．3×108元 C．3×1010元 D．0.3×1010元
4．衢州市2021届初中毕业生体育与健康考试中运动技能素质新增一分钟跳绳选测项目，据统计，某校九（3）班学生在一次跳绳模拟考试中，一组7人一分钟跳的次数依次是：186，178，185，182，186，176，188．这组数据的中位数和众数分别是（　　）
A．182和186 B．182和178 C．185和186 D．185和188
5．关于x的一元二次方程3x2﹣4x+8＝0的根的情况是（　　）
A．有两个相等的实数根 B．有两个不相等的实数根
C．只有一个实数根 D．没有实数根
6．已知实数a、b、c满足a＜b＜c，并且k＝++，则直线y＝﹣kx+k一定经过（　　）
A．第一、三、四象限 B．第一、二、四象限
C．第一、二、三象限 D．第二、三、四象限
7．如图，在△ABC中，∠C＝90°，点D是线段AB的垂直平分线与BC的交点，连接AD．若CD＝2，BD＝4，则AC的长为（　　）

A．4 B．3 C．2 D．
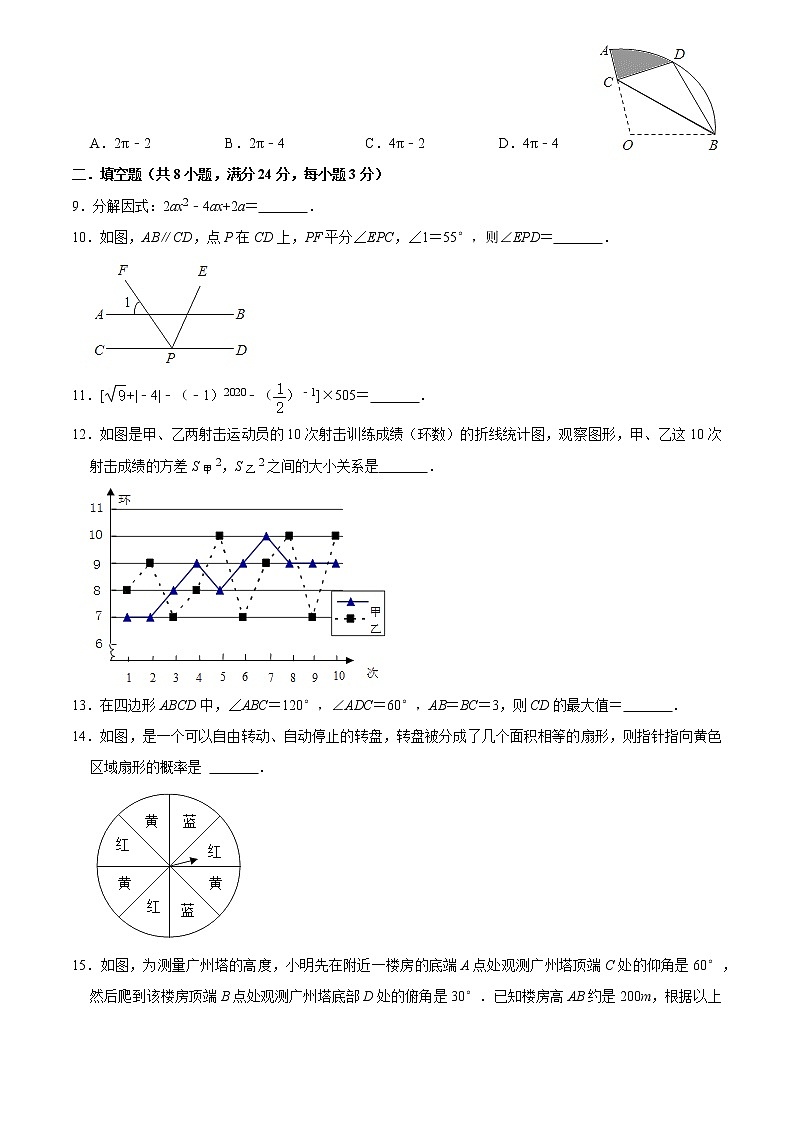
8．如图，在扇形OAB中，∠AOB＝105°，OA＝4，将扇形OAB沿着过点B的直线折叠，点O恰好落在的点D处，折痕BC交OA于点C，则阴影部分的面积为（　　）

A．2π﹣2 B．2π﹣4 C．4π﹣2 D．4π﹣4
二．填空题（共8小题，满分24分，每小题3分）
9．分解因式：2ax2﹣4ax+2a＝　 　．
10．如图，AB∥CD，点P在CD上，PF平分∠EPC，∠1＝55°，则∠EPD＝　 　．

11．[+|﹣4|﹣（﹣1）2020﹣（）﹣1]×505＝　 　．
12．如图是甲、乙两射击运动员的10次射击训练成绩（环数）的折线统计图，观察图形，甲、乙这10次射击成绩的方差S甲2，S乙2之间的大小关系是　 　．

13．在四边形ABCD中，∠ABC＝120°，∠ADC＝60°，AB＝BC＝3，则CD的最大值＝　 　．
14．如图，是一个可以自由转动、自动停止的转盘，转盘被分成了几个面积相等的扇形，则指针指向黄色区域扇形的概率是 　 　．

15．如图，为测量广州塔的高度，小明先在附近一楼房的底端A点处观测广州塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测广州塔底部D处的俯角是30°．已知楼房高AB约是200m，根据以上观测数据可求广州塔的高CD是 　 　m．

16．如图，小聪用一张面积为1的正方形纸片，按如下方式操作：
①将正方形纸片四角向内折叠，使四个顶点重合，展开后沿折痕剪开，把四个等腰直角三角形扔掉；②在余下纸片上依次重复以上操作，当完成第2019次操作时，余下纸片的面积为 　 　．

三．解答题（共6小题，满分36分，每小题6分）
17．如图，△ABC三个顶点的坐标分别为A（1，1）、B（4，2）、C（3，4）．
（1）画出△ABC关于y轴的对称图形△A1B1C1，并写出B1点的坐标；
（2）画出△ABC绕原点O旋转180°后得到的图形△A2B2C2，并写出B2点的坐标；
（3）在x轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标．

18．先化简，再求值：（1﹣）÷，其中x＝﹣1．
19．解不等式组：．
20．某超市计划购进一批甲、乙两种玩具，已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元，2件甲种玩具的进价与3件乙种玩具的进价的和为141元．
（1）求每件甲种、乙种玩具的进价分别是多少元；
（2）如果某超市计划购进一批甲、乙两种玩具共20件，其中甲的数量不少于乙种数量的2倍，请问该超市如何采购，至少要投入多少元才能完成采购计划？
21．已知在□ABCD中，AE⊥BC于E，DF平分∠ADC 交线段AE于F．
（1）如图1，若AE＝AD，∠ADC＝60°，请直接写出线段CD与AF+BE之间所满足等量关系；
（2）如图2，若AE＝AD，你在（1）中得到的结论是否仍然成立，若成立，对你的结论加以证明，若不成立，请说明理由；
（3）如图3，若AE：AD＝a：b，试探究线段CD、AF、BE之间所满足的等量关系，请直接写出你的结论．

22．为推进特色学校创建工作，丰富通学生们的体育活动，某校决定成立篮球、乒乓球、排球、足球、羽毛球社团，为了解学生对这些项目的喜爱情况，学校体育组老师随机抽取了部分学生进行调查，被调查的学生只能从篮球（记为A）、乒乓球（记为B）、排球（记为C）、足球（记为D）、羽毛球（记为E）选择一项．根据调查结果绘制成如图所示的两幅不完整的统计图．

请根据图中信息解答下列问题：
（1）在这项调查中，共调查了多少名学生？
（2）将条形统计图补充完整，并求出扇形统计图中“B”所在扇形圆心角的度数；
（3）若选择“E”的学生中有2名女生，其余为男生，现从选择“E”的学生中随机选出两名学生参加表演赛，请直接写出选到同性别学生的概率．
四．解答题（共4小题，满分36分，其中23、24题每题8分，25、26题每题10分）
23．如图，AB是⊙O的直径，点C是⊙O上一点，连接AC，BC，AD与⊙O相切于点A，交BC的延长线于点D，点E是劣弧BC的中点，连接AE，CE．
（1）求证：∠DAC＝∠AEC；
（2）延长CE，AB交于点G，使得GB＝AB，若AC＝2，求⊙O的半径．

24．如图，一次函数y1＝kx+b的图象分别交x轴，y轴于A，B两点，交反比例函数y2＝的图象于C，D两点，B（0，3），D（2，﹣1）．
（1）求一次函数与反比例函数的表达式；
（2）请直接写出当y2≥y1时，x的取值范围；
（3）点E为反比例函数y2＝的图象上一点，横坐标为m，若将点E向右平移2个单位后刚好落在一次函数y1＝kx+b的图象上，求m的值．

25．如图1是一种客厅放置的创意书架，共分三层，忽略其厚度，其基本结构可简化为图2，量得△ABC为等边三角形，AB＝100cm，DE∥FG∥BC，AD＝DF＝BF．
（1）求书架的高度；
（2）现有一种圆柱形茶叶盒的底面直径为10cm，高为15cm，若要将此茶叶盒按图中所示方式自然摆放在下层，一排可摆放多少个这样的茶叶盒？（结果精确到整数．参考数据：≈1.7）

26．在平面直角坐标系xOy中，直线y＝kx﹣2k+6经过定点Q．
（1）直接写出点Q的坐标　 　；
（2）点M在第一象限内，∠QOM＝45°，若点M的横坐标与点Q的纵坐标相等（如图1），求直线QM的解析式；
（3）在（2）条件下，过点M作MA⊥x轴于点A，过点Q作QB⊥y轴于点B，点E为第一象限内的一动点，∠AEO＝45°，点C为OB的中点（如图2），求线段CE长度的最大值．


参考答案与试题解析
一．选择题
1．【解答】解：∵|﹣3|＝3，|﹣2|＝2，|﹣|＝，而3＞2，
∴，
∴比﹣2小的是﹣3．
故选：B．
2．【解答】解：A、俯视图为圆，故此选项不合题意；
B、俯视图为圆，故此选项不合题意；
C、俯视图为三角形，故此选项不合题意；
D、俯视图为矩形，正确；
故选：D．
3．【解答】解：300亿元＝30000000000＝3×1010，
故选：C．
4．【解答】解：这组数据按照从小到大的顺序排列为：176，178，182，185，186，186，188，
则中位数为：185，
众数为：186，
故选：C．
5．【解答】解：根据题意得：
Δ＝（﹣4）2﹣4×3×8
＝16﹣96
＝﹣80＜0，
∴该方程没有实数根，
故选：D．
6．【解答】解：∵a＜b＜c，
∴c﹣a＞b﹣a＞0，
∴，
∵k＝++，
∴k＝++＜++＝＜0，
∴直线y＝﹣kx+k经过第一、三、四象限，
故选：A．
7．【解答】解：∵点D是线段AB的垂直平分线与BC的交点，BD＝4，
∴AD＝BD＝4，
在Rt△ACD中，CD＝2，AD＝4，
∴AC＝＝＝2，
故选：C．
8．【解答】解：连接OD，如右图所示，
∵将扇形OAB沿着过点B的直线折叠，点O恰好落在的点D处，
∴OB＝DB，OC＝DC，
∴∠COD＝∠CDO，
∵OD＝OB，∠AOB＝105°，
∴OB＝OD＝DB，
∴△OBD是等边三角形，∠BOD＝60°，
∴∠COD＝∠AOB﹣∠BOD＝105°﹣60°＝45°，
∴∠CDO＝45°，
∴∠OCD＝90°，
∵OD＝OA＝4，
∴OC＝CD＝2，
∴阴影部分的面积为：S扇形AOD﹣S△OCD＝＝2π﹣4，
故选：B．

二．填空题
9．【解答】解：原式＝2a（x2﹣2x+1）
＝2a（x﹣1）2．
故答案为：2a（x﹣1）2．
10．【解答】解：∵AB∥CD，∠1＝55°，
∴∠1＝∠CPF＝55°，
∵PF是∠EPC的平分线，
∴∠CPE＝2∠CPF＝110°，
∴∠EPD＝180°﹣110°＝70°，
故答案为：70°．
11．【解答】解：原式＝（3+4﹣1﹣2）×505＝4×505＝2020，
故答案为：2020．
12．【解答】解：由图可知甲的成绩为7，7，8，9，8，9，10，9，9，9，
乙的成绩为8，9，7，8，10，7，9，10，7，10，
甲的平均数是：（7+7+8+9+8+9+10+9+9+9）÷10＝8.5，
乙的平均数是：（8+9+7+8+10+7+9+10+7+10）÷10＝8.5，
甲的方差S甲2＝[2×（7﹣8.5）2+2×（8﹣8.5）2+（10﹣8.5）2+5×（9﹣8.5）2]÷10＝0.85，
乙的方差S乙2＝[3×（7﹣8.5）2+2×（8﹣8.5）2+2×（9﹣8.5）2+3×（10﹣8.5）2]÷10＝1.45
则S2甲＜S2乙．
故答案为：S甲2＜S乙2．
13．【解答】解：∵∠ABC＝120°，∠ADC＝60°，
∴∠ABC+∠ADC＝180°，
∴四边形ABCD是圆内接四边形，
∴当CD是直径时，CD达到最大值，
连接OA，OB，
∵OA＝OD，∠ADC＝60°，
∴△AOD是等边三角形，
∴∠AOD＝60°，
∵∠ABC＝120°，AB＝BC＝3，
∴∠AOB＝∠BOC＝60°，
∵OA＝OB＝OC，
∴△AOB和△BOC都是等边三角形，
∴OC＝BC＝3，
∴CD＝2OC＝6，
故答案为：6．

14．【解答】解：∵转盘被分成了8个面积相等的扇形，其中黄色部分占3份，
∴指针指向黄色区域扇形的概率是．
故答案为：．
15．【解答】解：由题意可知，∠ABD＝90°﹣30°＝60°，∠CAD＝60°，AB＝200m，
Rt△ABD中，AB＝200m，∠ABD＝60°，
∴AD＝AB＝200（m），
在Rt△ACD中，AD＝200m，∠CAD＝60°，
∴CD＝AD＝600（m），
故答案为：600．
16．【解答】解：正方形纸片四角向内折叠，使四个顶点重合，展开后沿折痕剪开，
第一次：余下面积S1＝，
第二次：余下面积S2＝，
第三次：余下面积S3＝，
当完成第2019次操作时，余下纸片的面积为S2019＝，
故答案为：．
三．解答题
17．【解答】解：（1）△A1B1C1如图所示，
B1（﹣4，2）；

（2）△A2B2C2如图所示，
B2（﹣4，﹣2）；

（3）△PAB如图所示，
P（2，0）．

18．【解答】解：原式＝•
＝•
＝，
当x＝﹣1时，原式＝＝﹣2．
19．【解答】解：解不等式2x+5≤3（x+2），得：x≥﹣1，
解不等式2x﹣＜1，得：x＜3，
则不等式组的解集为﹣1≤x＜3．
20．【解答】解：（1）设每件甲种玩具的进价是x元，每件乙种玩具的进价是y元，
依题意得：，
解得：．
答：每件甲种玩具的进价是30元，每件乙种玩具的进价是27元．
（2）设购进甲种玩具m件，则购进乙种玩具（20﹣m）件，
依题意得：m≥2（20﹣m），
解得：m≥．
又∵m为正整数，
∴m的最小值为14，
∴该超市至少采购14件甲种玩具．
设该超市购进这批玩具共花费w元，则w＝30m+27（20﹣m）＝3m+540．
∵k＝3＞0，
∴w随m的增大而增大，
∴当m＝14时，w取得最小值，最小值＝3×14+540＝582，
∴该超市至少要投入582元才能完成采购计划．
21．【解答】（1）解：CD＝AF+BE，
理由是：延长EA到G，使得AG＝BE，连接DG，
∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，AD＝BC，
∵AE⊥BC，
∴∠AEB＝∠AEC＝90°，
∴∠AEB＝∠DAE＝90°，
∴∠DAG＝90°，
在△ABE和△DGA中

∴△ABE≌△DGA，
∴DG＝AB＝CD，∠1＝∠2，
∵平行四边形ABCD，AE⊥BC，
∴∠B＝∠ADC＝60°＝∠G，AE⊥AD，
∴∠1＝∠2＝30°，
∵DF平分∠ADC，
∴∠3＝∠4＝30°，
∴∠AFD＝60°＝∠GDF，
∴DG＝GF＝AF+AG，
∴CD＝AB＝DG＝AF+BE，
即CD＝AF+BE．

（2）解：（1）中的结论仍然成立．
证明：延长EA到G，使得AG＝BE，连接DG，
∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，AD＝BC，
∵AE⊥BC于点E，
∴∠AEB＝∠AEC＝90°，
∴∠AEB＝∠DAG＝90°，
∴∠DAG＝90°，
在△ABE和△DGA中

∴△ABE≌△DGA，
∴∠1＝∠2，DG＝AB，∠B＝∠G，
∵四边形ABCD是平行四边形，
∴∠B＝∠ADC，
∵∠B+∠1＝∠ADC+∠2＝90°，∠3＝∠4，
∴∠GDF＝90°﹣∠4，∠GFD＝90°﹣∠3，
∴∠GDF＝∠GFD，
∴GF＝GD＝AB＝CD，
∵GF＝AF+AG＝AF+BE，
∴CD＝AF+BE．

（3）bCD＝aAF+bBE
理由是：延长EA到G，使得＝，连接DG，
即AG＝BE，
∵四边形ABCD是平行四边形，
∴AB＝CD，AB∥CD，AD＝BC，
∵AE⊥BC于点E，
∴∠AEB＝∠AEC＝90°，
∴∠AEB＝∠DAG＝90°，
∴∠DAG＝90°，
即∠AEB＝∠GAD＝90°，
∵＝＝，
∴△ABE∽△DGA，
∴∠1＝∠2，＝，
∴∠GFD＝90°﹣∠3，
∵DF平分∠ADC，
∴∠3＝∠4，
∴∠GDF＝∠2+∠3＝∠1+∠4＝180°﹣∠FAD﹣∠3＝90°﹣∠3．
∴∠GDF＝∠GFD，
∴DG＝GF，
∵＝，AB＝CD（已证），
∴bCD＝aDG＝a（BE+AF），
即 bCD＝aAF+bBE．


22．【解答】解：（1）30÷20%＝150（人），
∴共调查了150名学生；
（2）D：50%×150＝75（人），B：150﹣30﹣75﹣24﹣6＝15（人），
补全条形图如图所示．

扇形统计图中“B”所在扇形圆心角的度数为360°×＝36°．
（3）记选择“E”的同学中的2名女生分别为N1，N2，4名男生分别为M1，M2，M3，M4，
列表如下：

N1
N2
M1
M2
M3
M4
N1

（N1，N2）
（N1，M1）
（N1，M2）
（N1，M3）
（N1，M4）
N2
（N2，N1）

（N2，M1）
（N2，M2）
（N2，M3）
（N2，M4）
M1
（M1，N1）
（M1，N2）

（M1，M2）
（M1，M3）
（M1，M4）
M2
（M2，N1）
（M2，N2）
（M2，M1）

（M2，M3）
（M2，M4）
M3
（M3，N1）
（M3，N2）
（M3，M1）
（M3，M2）

（M3，M4）
M4
（M4，N1）
（M4，N2）
（M4，M1）
（M4，M2）
（M4，M3）

∵共有30种等可能的结果，其中，恰好是同性别学生的有14种情况，
∴选到同性别学生的概率为＝．
四．解答题
23．【解答】（1）证明：∵AD是⊙O的切线，AB是⊙O的直径，
∴AD⊥AB．
∵AB是⊙O的直径，
∴∠ACB＝90°．
即AC⊥BD．
∴∠DAC＝∠ABC＝∠AEC．
即∠DAC＝∠AEC．

（2）解：过B作BF∥AC，交CG于F，连接OE．
∵BG＝AB，AC＝2，
∴BF＝AC＝×2＝．
∵点E是弧BC的中点，
∴OE⊥BC．
∵AC⊥BD，
∴OE∥AC．
∵O是AB的中点，
∴OE是梯形ABFC的中位线．
∴OE＝．
所以⊙O的半径为．
24．【解答】解：（1）把B（0，3），D（2，﹣1）代入一次函数y1＝kx+b得，
，解得，k＝﹣2，b＝3，
∴一次函数的关系式为y＝﹣2x+3，
把D（2，﹣1）代入反比例函数关系式得，a＝2×（﹣1）＝﹣2，
∴反比例函数的关系式为y＝﹣；
（2）由题意得，
，解得，，，
∵D（2，﹣1），
∴C（﹣，4），
根据图象可知，当y2≥y1时，x的取值范围为﹣≤x＜0或x≥2．
（3）设平移后落在y＝﹣2x+3上的对应点为E′，
则E（m，﹣），E′（m+2，﹣2m﹣1）
因此有：﹣＝﹣2m+1，
解得，m1＝，m2＝，
经检验，均符合题意，
故m的值为：或．
25．【解答】解：（1）过A作AH⊥BC，垂足为H，

∵△ABC是等边三角形，
∴∠B＝∠C＝60°，AB＝BC＝100cm，
在Rt△ABH中，AB＝100cm，
∴AH＝ABsin60°＝100×＝50≈85（厘米），
答：书架的高度约为85厘米；
（2）如图，设靠右侧摆放的茶叶盒的右侧与书架交于点M，P，

在Rt△MPC中，MP＝15cm，∠C＝60°，
∴CP＝＝＝5cm，
∴BC﹣2PC＝100﹣10≈83cm，
∴83÷10＝8.3，
∴一排可最多能摆放8个这样的茶叶盒．
26．【解答】解：（1）y＝kx﹣2k+6＝k（x﹣2）+6，
则当x﹣2＝0，即x＝2时，y的值与k无关，
则Q的坐标是（2，6）；
（2）方法一：如图4，过Q作QB⊥y轴于B，过M作MA⊥x轴于A，延长BQ，AM交于点F．连接OF，作QG⊥OF于点G．

则四边形AOBF是正方形，△QFG是等腰直角三角形，且OA＝OB＝BF＝AF＝6，BQ＝2，
则QF＝4，
∴QG＝QF×＝4×＝2，
在直角△OBQ中，OQ＝＝＝2，
∴直角△OQG中，OG＝＝＝4．
∵正方形AOBF中，∠AOB＝90°，∠AOF＝45°，
又∵∠QOM＝45°，
∴∠QOG+∠FOM＝∠FOM+∠AOM＝45°，
∴∠QOG＝∠AOM，
又∵∠OGQ＝∠OAM，
∴△OQG∽△OMA，
∴，即，
∴AM＝3，
∴M的坐标是（6，3）．
设直线QM的解析式是y＝kx+b，
则，
解得：，
则直线QM的解析式是：y＝﹣x+；
方法二：如图3．过点Q作QN垂直y轴于点N，将△NQO绕点O顺时针旋转90°，得到△HQ'O，连接MQ'；

∵Q的坐标是（2，6），
∴Q'坐标为：（6，﹣2），
又∵点M的横坐标与点Q的纵坐标相等，
∴M、H、Q'三点共线，设M（6，m），
∵∠QOM＝45°，∠NOH＝90°，
∴∠NOQ+∠MOH＝45°，
又∵∠NOQ＝∠Q'OH，
∴∠MOQ'＝45°．
在△QOM和△Q'OM中，

∴△QOM≌△Q'OM（SAS）
∴QM＝Q'M
∴，m＝3，
∴M的坐标是（6，3）．
设直线QM的解析式是y＝kx+b，
则，
解得：，
则直线的解析式是：y＝﹣x+；
（3）解法一：如图5，延长BQ，AM交于点D，则四边形AOBD是正方形，连接ED，过点A作AF⊥AE，交OE于点F，连接OD，取OD的中点为H，连接CH，EH，

∴AO＝AD，
∵∠AEO＝45°，
∴△AEF是等腰直角三角形，AE＝AF，∠OAF＝∠DAE，
∴△DAE≌△OAF（SAS），
∴∠AED＝∠AFO＝135°，
∴∠DEO＝135°﹣45°＝90°，
∵H是OD的中点，
∴EH＝OD＝3，
∵C是OB的中点，
∴CH＝BD＝3，
△CEH中，CH+EH≥CE，
∴CE≤3+3，
∴当C、E、H三点共线时，线段CE最长，则最大的长度是：3+3．

解法二：∵∠AEO＝45，
∴E在以OA为斜边的等腰直角三角形直角顶点为圆心，以OA为弦的圆上，且弦OA所对的圆心角是90°的圆上，设圆心是N，则N的坐标是（3，3），圆的半径是3，
又∵点C为OB的中点，
∴C的坐标是（0，3），
则CN∥x轴，
则当E是CN的延长线与圆N的交点时，线段CE最长，则最大的长度是：3+3．