人教B版 (2019)必修 第三册7.3.4 正切函数的性质与图修学案及答案
展开正切函数的图象与性质
【学习目标】
1.能画出y=tan x的图象,借助图象理解正切函数在区间上的性质.
2.掌握正切函数的性质,会求正切函数的定义域、值域及周期,会用函数的图象与性质解决综合问题.
【学习重难点】
掌握正切函数的性质,会求正切函数的定义域、值域及周期.
【学习过程】
一、初试身手
1.函数y=-3tan x+7的值域是( )
A.R
B.{x|x≠kπ+,k∈Z}
C.(0,+∞)
D.(k∈Z)
2.y=tan定义域为________.
3.函数y=tan的单调增区间为________.
二、合作探究
1.正切函数的定义域、值域问题
【例1】(1)函数y=+lg(1-tan x)的定义域是________.
(2)函数y=tan(sin x)的值域为________.
(3)求函数y=-tan2 x+2tan x+5,x∈的值域.
2.正切函数的奇偶性、周期性
【例2】(1)函数y=4tan的周期为________.
(2)判断下列函数的奇偶性:
①f(x)=;
②f(x)=tan+tan.
3.正切函数的单调性
[探究问题]
(1) 正切函数y=tan x在其定义域内是否为增函数?
(2) 正切函数的定义域能写成,(k∈Z)吗?为什么?
【例3】(1)求函数y=tan的单调区间;
(2)比较tan 1,tan 2,tan 3的大小.
【学习小结】
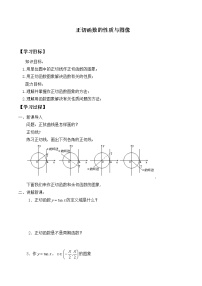
1.正切函数的图象
(1)正切函数的图象:
y=tan x的图象如图.
(2)正切函数的图象叫做正切曲线.
(3)正切函数的图象特征:
正切曲线是由通过点(k∈Z)且与y轴平行的直线隔开的无穷多支曲线所组成.
2.正切函数的性质
(1)函数y=tan x的图象与性质表:
解析式 | y=tan x |
图象 | |
定义域 |
|
值域 | R |
周期 | π |
奇偶性 | 奇函数 |
单调性 | 在开区间k∈Z内都是增函数 |
(2)函数y=tan ωx(ω≠0)的最小正周期是.
【精炼反馈】
1.函数y=tan x的值域是( )
A.[-1,1] B.[-1,0)∪(0,1]
C.(-∞,1] D.[-1,+∞)
2.直线y=3与函数y=tan ωx(ω>0)的图象相交,则相邻两交点间的距离是( )
A.π B.
C. D.
3.函数f(x)=tan的定义域是________,f=________.
4.函数y=-tan x的单调递减区间是________.
5.求下列函数的定义域:
(1)y=;
(2)y=lg(-tan x).
数学必修 第三册7.3.4 正切函数的性质与图修导学案: 这是一份数学必修 第三册7.3.4 正切函数的性质与图修导学案,共4页。学案主要包含了学习目标,学习过程等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第三册7.3.4 正切函数的性质与图修学案: 这是一份高中数学人教B版 (2019)必修 第三册7.3.4 正切函数的性质与图修学案,共5页。学案主要包含了学习目标,学习重难点,学习过程等内容,欢迎下载使用。
数学7.3.4 正切函数的性质与图修导学案: 这是一份数学7.3.4 正切函数的性质与图修导学案,共2页。学案主要包含了学习目标,学习过程等内容,欢迎下载使用。