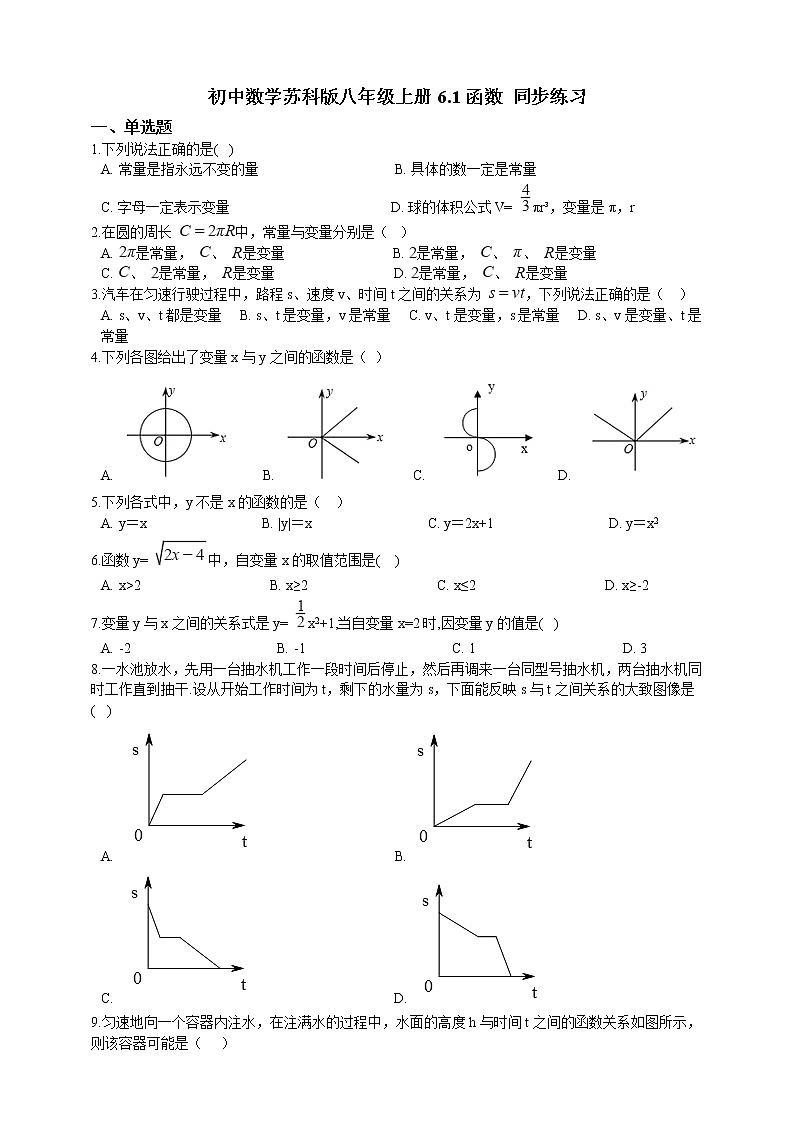

苏科版八年级上册6.1 函数课后作业题
展开初中数学苏科版八年级上册6.1函数 同步练习
一、单选题
1.下列说法正确的是( )
A. 常量是指永远不变的量 B. 具体的数一定是常量
C. 字母一定表示变量 D. 球的体积公式V= πr³,变量是π,r
2.在圆的周长 中,常量与变量分别是( )
A. 是常量, 、 是变量 B. 是常量, 、 、 是变量
C. 、 是常量, 是变量 D. 是常量, 、 是变量
3.汽车在匀速行驶过程中,路程s、速度v、时间t之间的关系为 ,下列说法正确的是( )
A. s、v、t都是变量 B. s、t是变量,v是常量 C. v、t是变量,s是常量 D. s、v是变量、t是常量
4.下列各图给出了变量x与y之间的函数是( )
A. B. C. D.
5.下列各式中,y不是x的函数的是( )
A. y=x B. |y|=x C. y=2x+1 D. y=x2
6.函数y= 中,自变量x的取值范围是( )
A. x>2 B. x≥2 C. x≤2 D. x≥-2
7.变量y与x之间的关系式是y= x2+1,当自变量x=2时,因变量y的值是( )
A. -2 B. -1 C. 1 D. 3
8.一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作时间为t,剩下的水量为s,下面能反映s与t之间关系的大致图像是( )
A. B.
C. D.
9.匀速地向一个容器内注水,在注满水的过程中,水面的高度h与时间t之间的函数关系如图所示,则该容器可能是( )
A. B. C. D.
10.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/时,特快车的速度为150千米/时,甲乙两地相距1500千米,两车同时出发,则图中折线可以表示两车之间的距离y(千米)与快车行驶时间t(小时)之间函数关系的图象的是( )
A. B.
C. D.
二、填空题
11.下列各项:① ;② ;③ ;④ ;具有函数关系(自变量为 )的是________.(填序号)
12.在关系式y=2x2+x+1中,可把________看成________的函数,其中________是自变量,________是因变量.
13.矩形的面积为S,则长a和宽b之间的关系为S=________,当长一定时,________是常量,________是变量.
14.如图是汽车加油站在加油过程中,加油器仪表某一瞬间的显示,请你结合图片信息,解答下列问题:
(1)加油过程中的常量是________ ,变量是________ ;
(2)请用合适的方式表示加油过程中变量之间的关系________
15.如果y=(m+2)x+m﹣1是常值函数,那么m=________
16.在3x﹣2y=6中,把它写成x是y的函数为________.
17.某自行车存车处在星期日的存车为4000辆次,其中变速车存车费是每辆一次0.3元,普通车存车费是每辆一次0.2元,若普通车存车数为x辆次,存车总收入y(元)与x的函数关系式是________.
18.等腰△ABC的周长为10厘米,底边BC长为y厘米,腰AB长为x厘米,则y与x的关系式为:________.当x=2厘米时,y=________厘米;当y=4厘米时,x=________厘米.
三、解答题
19.分析并指出下列关系中的变量与常量:
(1)球的表面积S cm2与球的半径R cm的关系式是S=4πR2;
(2)以固定的速度v0米/秒向上抛一个小球,小球的高度h米与小球运动的时间t秒之间的关系式是h=v0t﹣4.9t2;
(3)一物体自高处自由落下,这个物体运动的距离h m与它下落的时间t s的关系式是h=gt2(其中g取9.8m/s2);
(4)已知橙子每千克的售价是1.8元,则购买数量W千克与所付款x元之间的关系式是x=1.8W.
20.当自变量x取何值时,函数y= x+1与y=5x+17的值相等?这个函数值是多少?
21.如图,在靠墙(墙长8m)的地方围建一个矩形的养鸡场,另外三边用栅栏围成,如果栅栏总长为32m,求鸡场的一边y(m)与另一边x(m)的函数关系式,并求出自变量的取值范围.
22.按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
23.下表给出了橘农王林去年橘子的销售额(元)随橘子卖出质量(千克)的变化的有关数据:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是多少?
(3)估计当橘子卖出50千克时,销售额是多少?
24.求下列函数中自变量的取值范围.
(1)
(2)
(3)
(4)
(5)
25.写出下列各问题中的函数关系式,并指出自变量的取值范围.
(1)如果直角三角形中一个锐角的度数为α,另一个锐角的度数β与α之间的关系;
(2)一支蜡烛原长为20cm,每分钟燃烧0.5cm,点燃x(分钟)后,蜡烛的长度y(cm)与x(分钟)之间的关系;
(3)有一边长为2cm的正方形,若其边长增加xcm,则增加的面积y(cm2)与x之间的关系.
26.“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明家、新华书店、学校在一条笔直的公路旁,某天小明骑车上学,当他骑了一段后,想起要买某本书, 于是又折回到刚经过的新华书店,买到书后继续骑车去学校,他本次骑车上学的过程中离家距离与所用的时间的关系如图所示,请根据图象提供的信息回答下列问题:
(1)小明家到学校的距离是________米;
(2)小明在书店停留了________分钟;
(3)本次上学途中,小明一共骑行了________米;
(4)我们认为骑车的速度超过了 米/分就超越了安全限度,小明买到书后继续骑车到学校的这段时间的骑车速度在安全限度内吗?请说明理由,
答案解析部分
一、单选题
1.【答案】B
解:A、常量和变量是相对于变化过程而言的.可以互相转化,不符合题意;
B、具体的数一定为常量,符合题意;
C、字母π是一个常量,不符合题意;
D、π是常量,不符合题意,
故答案为:B.
【分析】在某一变化过程中,不变的量是常量,不断变化的量是变量。根据常量和变量的意义可判断。
2.【答案】 A
解: 中 是始终不变的, 是常量; 、 是会发生变化的,是变量.
故答案为:A
【分析】利用变量和常量的定义,可知C随着R的变化而变化,即可的此变化过程中的常量与变量。
3.【答案】 B
解:汽车在匀速行驶过程中,速度不变,是常量,t、s是变量.
故答案为:B.
【分析】利用变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量进行分析.
4.【答案】 D
解:A、B、C中对于x的值y的值不是唯一的,因而不符合函数的定义;
D、符合函数定义.
故答案为:D.
【分析】根据函数的定义,选项A、B、C中对于x的值y的值不是唯一的,不符合函数的定义,
选项D符合函数定义,即可求解.
5.【答案】 B
解:A、y=x,y是x的函数,故此选项不符合题意;
B、|y|=x,对于x的每一个确定的值,y不是有唯一的值与其对应,
∴y不是x的函数,故此选项符合题意;
C、y=2x+1,y是x的函数,故此选项不符合题意;
D、y=x2 , y是x的函数,故此选项不符合题意;
故答案为:B.
【分析】直接利用函数的概念:在一个变化过程中的两个变量 ,对于变量 的每一个值, 都有唯一的一个值与之对应,则 是 的函数,逐一分析每个选项得出答案.
6.【答案】 B
解:由题意得:2x-4≥0.
解之:x≥2.
故答案为:B.
【分析】观察此函数解析式中含自变量的式子是二次根式,因此被开方数是非负数,即可建立关于x的不等式,解不等式可求出x的取值范围。
7.【答案】 D
解:∵ ,
∴当 时, .
故答案为:D.
【分析】由题意把x=2代入解析式计算即可求解。
8.【答案】 D
解:由题意知,随着抽水时间的增加,剩下水量逐渐减少;而停止时水量不变,两台抽水机同时工作抽水速度增大,即直线斜率增大,剩下的水量减少更快,据此逐段分析可得答案.
故答案为:D.
【分析】由于随着抽水时间的增加,剩下水量逐渐减少;停止时水量不变,两台抽水机同时工作抽水速度增大,剩下的水量减少更快;根据这三段所表示的意义结合图象即可判断.
9.【答案】 D
解:设某段圆柱截面积为S,单位时间的注水量为v, 则V=SH=vt,
∴H==kt,
∵这是一个正比例函数,当S越大时,k越小,H随时间t增大而增大得越快,当S越小时,k越大,H随t增大而增大得越慢,由图象可得开始一段时间水位上升较快,后来一段时间水位上升较慢,
∴容器的下部截面积较小,上部截面积较大,D符合题意.
故答案为:D.
【分析】设某段圆柱截面积为S,单位时间的注水量为v, 可得H==kt, 得出k值的大小,即直线的上升快慢跟截面积S的关系,再结合图象分析即可解答.
10.【答案】 C
解:①两车从开始到相遇,这段时间两车距迅速减小;
②相遇后向相反方向行驶到特快到达甲地这段时间两车距迅速增加;
③特快到达甲地至快车到达乙地,这段时间两车距缓慢增大;
结合图象可得C选项符合题意.
故答案为:C.
【分析】分三段讨论,①两车从开始到相遇,这段时间两车距迅速减小,②相遇后向相反方向行驶到特快到达甲地,这段时间两车距迅速增加,③特快到达甲地至快车到达乙地,这段时间两车距缓慢增大,结合实际选符合的图象即可.
二、填空题
11.【答案】 ①②④
解:∵对于x的每一个取值,y都有唯一确定的值,
∴①y=x2;②y=2x-1④ 当x取值时,y有唯一的值对应;
而③ ,例如当x=2时,y=±2,不具有唯一值.
故具有函数关系(自变量为x)的是①②④.
故答案为①②④
【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定哪些是函数.
12.【答案】y;x;x;y
解:可把y看成x的函数, 其中x是自变量,y是因变量.
【分析】根据函数的概念,对于每一个x的值,y都有唯一的值和它相对应,而反之则不成立.
13.【答案】ab;a;S,b
解:由题意得:S=ab, 在该关系式中,当长一定时,a是常量,S,b是变量.
故答案为:ab;a;S,b.
【分析】根据题意先列出函数关系式,再根据函数的意义可知:变量是改变的量,常量是不变的量,据此即可确定变量与常量.
14.【答案】单价;数量、金额;y=6.80x
解:(1)加油过程中的常量是单价,变量是数量、金额;
故答案为:单价,数量、金额.
(2)设加油数量是x升,金额是y元,
则y=6.80x.
【分析】(1)根据常量和变量的定义,即可解答;
(2)根据金额=单价×数量,即可列出
15.【答案】-2
解:由题意得,m+2=0,
m=﹣2,
故答案为:﹣2.
【分析】因为y=(m+2)x+m﹣1是常值函数,所以m+2=0,即可求得m的值.
16.【答案】x=
解:等式变形可得: x= .
【分析】根据题意把3x﹣2y=6写成x是y的函数,把x写在等号的左边,其他项移到等号右边即可.
17.【答案】y=﹣0.1x+1200
解:根据题意可知,存车总收入y(元)与x的函数关系式是y=0.2x+(4000﹣x)×0.3=﹣0.10x+1200. ∴函数关系式为:y=﹣0.1x+1200
【分析】先根据普通车存车数为x辆求出变速车的辆数,再根据其价格即可列出函数关系式.
18.【答案】y=10﹣2x(0<x<5);6;3
解:由题意得10=y+2x, 即y=10﹣2x(0<x<5);
当x=2时y=10﹣4=6;
当y=4时,4=10﹣2x,x=3.
【分析】先根据题意写出关系式,再把x=2,y=4分别代入即可.
三、解答题
19.【答案】 解:(1)球的表面积S cm2与球的半径R cm的关系式是S=4πR2 , 其中,常量是4π,变量是S,R;
(2)以固定的速度v0米/秒向上抛一个小球, 小球的高度h米与小球运动的时间t秒之间的关系式是h=v0t﹣4.9t2 , 常量是v0 , 4.9,变量是h,t;
(3)一物体自高处自由落下,这个物体运动的距离h m与它下落的时间t s的关系式是h=gt2(其中g取9.8m/s2)其中常量是g,变量是h,t;
(4)已知橙子每千克的售价是1.8元,则购买数量W千克与所付款x元之间的关系式是x=1.8W,常量是1.8,变量是x,w.
【分析】根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可直接得到答案
20.【答案】解:由题意得 ,解得 , 当x=﹣ 时,函数y= x+1与y=5x+17的值相等,这个函数值是﹣15
【分析】根据函数值相等,自变量相等,可得方程组,根据解方程组,可得答案.
21.【答案】 解:(1)根据题意得:鸡场的长y(m)与宽x(m)有
y+2x=32:即y=-2x+32;(2)题中有8>y>0,-2x+32≤8
∴x≥12
又y>x
-2x+35>x,解得x<16
则自变量的取值范围为故答案为: 12≤x<16.
【分析】根据长方形的面积公式和围成的长方形仅有三边,找到函数关系解答即可
22.【答案】 解:(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x﹣1)=4x+2个座位.
故可坐人数y=4x+2,
故答案为:有2个变量;
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
【分析】由图形可知,第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.x张餐桌共有6+4(x﹣1)=4x+2.
23.【答案】 解:(1)表中反映了橘子的卖出质量与销售额之间的关系, 橘子的卖出质量是自变量,销售额是因变量;
(2)当橘子卖出5千克时,销售额为10元;
(3)当橘子卖出50千克时,销售额为100元
【分析】(1)根据表格发现反映的是卖出质量和销售额之间的关系;
(2)观察表格会发现数据5对应的是10,从而得到答案;
(3)用单价乘以卖出量即可求得销售额.
24.【答案】 (1)解: 的取值范围为全体实数
(2)解:解不等式 ,得 ,故x的取值范围为
(3)解:解不等式 ,得 ,故x的取值范围为
(4)解:解不等式 ,得 ,故x的取值范围为
(5)解:解不等式组 得 ,故x的取值范围为
【分析】(1)中的解析式自变量的取值范围是全体实数;
(2)中的解析式分母不能为零,即x-4≠0;
(3)中的解析式被开方数为非负数,即2x-4≥0;
(4)中的解析式即要满足被开方数为非负数,又要满足分母不能为零,即x+3>0;
(5)中的解析式有两个被开方数,这两个被开方数都为非负数,可以得到一个一元一次不等式组,即x-1≥0,6-2x≥0。
25.【答案】 (1)解:β=90°-α,
∵α>0,β>0
∴0°<α<90°
(2)解:y=20-0.5x,
∵20-0.5x≥0,x≥0
∴0≤x≤40
(3)解:y=(x+2)2-22=x2+4x,x>0.
【分析】(1)由“直角三角形的两个锐角互余”来写函数关系式;(2)根据点燃后蜡烛的长度=原长−燃烧的长度,列函数关系式;(3)根据正方形增加的面积=新正方形的面积−原正方形的面积.
26.【答案】 (1)1500
(2)4
(3)2700
(4)解:由图象可知:12~14分钟时,平均速度为: 米/分,
∵450>300,
∴12~14分钟时速度最快,不在安全限度内
解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0,
故小明家到学校的路程是1500米;
故答案为:1500;(2)根据题意,小明在书店停留的时间为从8~12分钟,
故小明在书店停留了4分钟.
故答案为:4;(3)一共行驶的总路程=1200+(1200-600)+(1500-600)
=1200+600+900=2700米;
故答案为:2700;
【分析】(1)根据函数图象的纵坐标,可得答案;(2)根据函数图象的横坐标,可得到达书店时间,离开书店时间,根据有理数的减法,可的答案;(3)根据函数图象的纵坐标,可得相应的路程,根据有理数的加法,可得答案;(4)根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得速度.
苏科版八年级上册6.1 函数同步练习题: 这是一份苏科版八年级上册6.1 函数同步练习题,共9页。
初中数学苏科版八年级上册6.3 一次函数的图像习题: 这是一份初中数学苏科版八年级上册6.3 一次函数的图像习题,共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2021学年6.2 一次函数课后作业题: 这是一份2021学年6.2 一次函数课后作业题,共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













