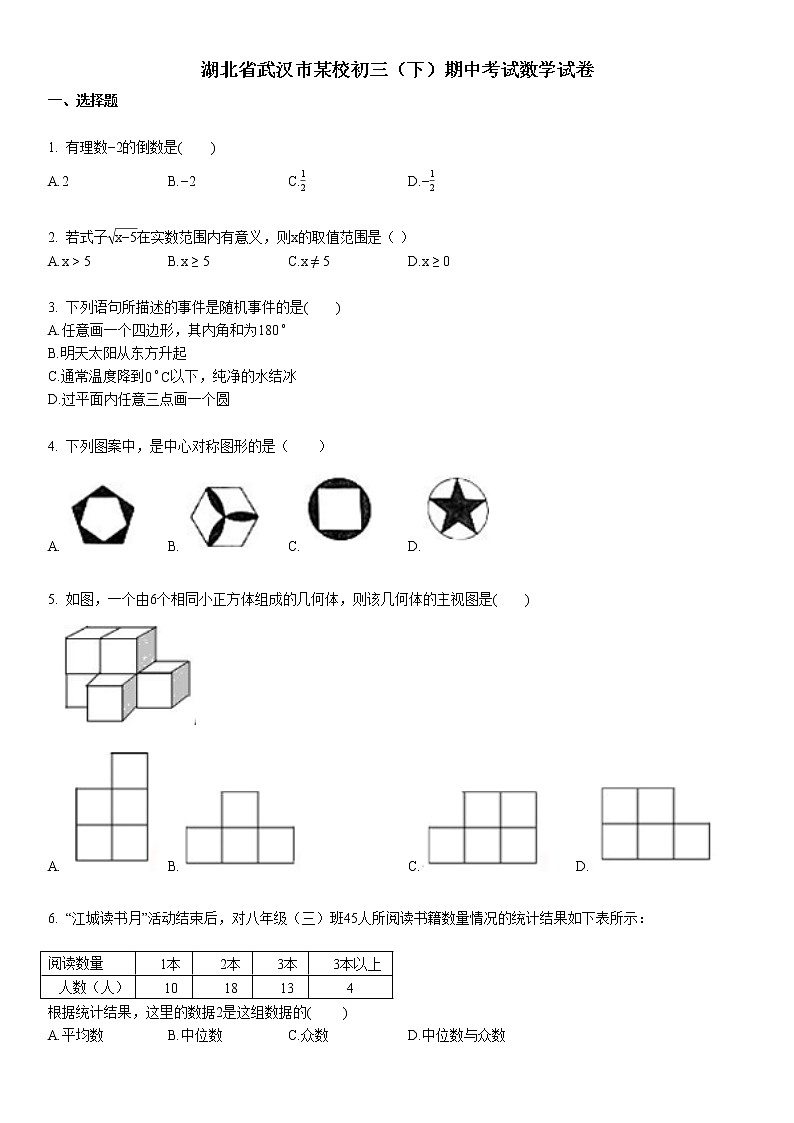
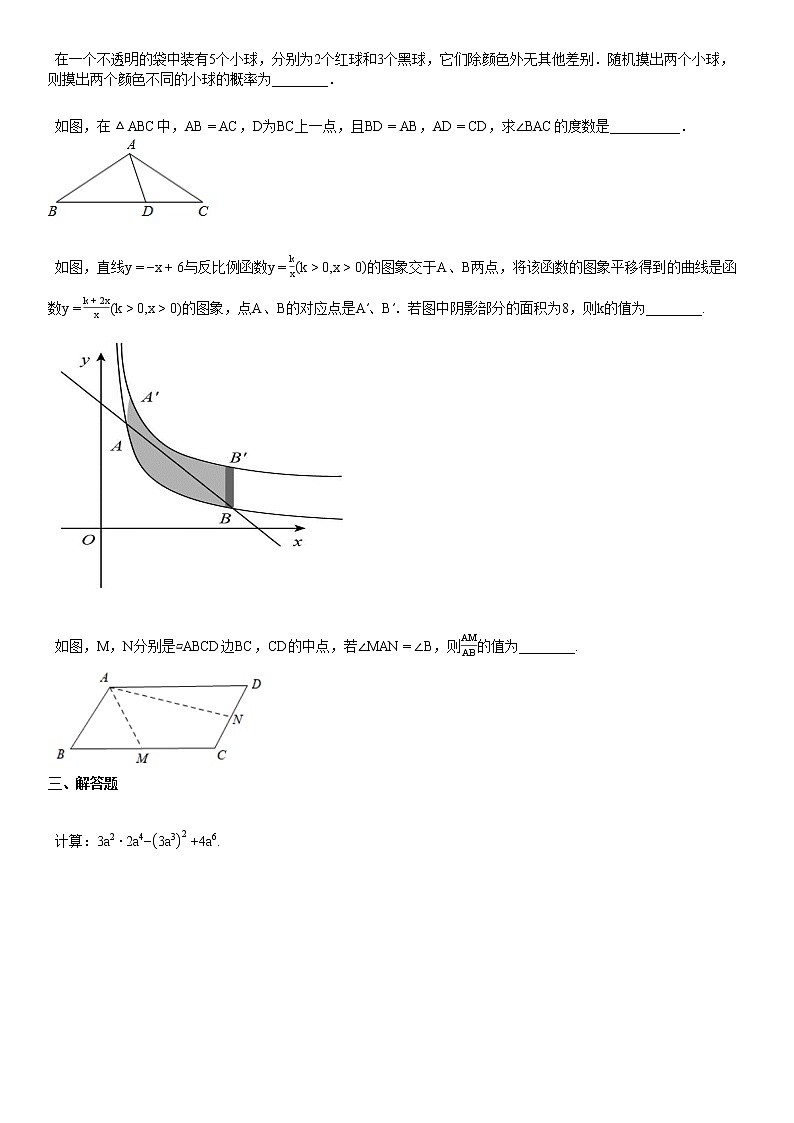
2019-2020学年湖北省武汉市某校初三（下）期中考试数学试卷

这是一份2019-2020学年湖北省武汉市某校初三（下）期中考试数学试卷，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 有理数−2的倒数是( )
A.2B.−2C.12D.−12

2. 若式子x−5在实数范围内有意义，则x的取值范围是（ ）
A.x>5B.x≥5C.x≠5D.x≥0

3. 下列语句所描述的事件是随机事件的是( )
A.任意画一个四边形，其内角和为180∘
B.明天太阳从东方升起
C.通常温度降到0∘C以下，纯净的水结冰
D.过平面内任意三点画一个圆

4. 下列图案中，是中心对称图形的是（ ）
A.B.C.D.

5. 如图，一个由6个相同小正方体组成的几何体，则该几何体的主视图是( )

A.B.C.D.

6. “江城读书月”活动结束后，对八年级（三）班45人所阅读书籍数量情况的统计结果如下表所示：
根据统计结果，这里的数据2是这组数据的( )
A.平均数B.中位数C.众数D.中位数与众数

7. 甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，则可以列方程组是( )
A.11x=9y(10y+x)−(8x+y)=13
B.10y+x=8x+y9x+13=11y
C.9x=11y(8x+y)−(10y+x)=13
D.9x=11y(10y+x)−(8x+y)=13

8. 已知抛物线y=−(x−1)2+m（m是常数），点A(x1, y1)，B(x2, y2)在抛物线上，若x1<12，则m，y1，y2的大小关系的是( )
A.m>y1>y2B.m>y2>y1C.y1>y2>mD.y2>y1>m

9. 如图，△ABC中，∠A=30∘，点O是边AB上一点，以点O为圆心，OB为半径的⊙O恰好与AC相切于点D，连接BD，若BD平分∠ABC，AD=23，则线段CD的长是( )

A.2B.3C.32D.323

10. 我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉（约13世纪）所著的《详解九章算术》一书中，用如图的三角形解释二项式(a+b)n的展开式的各项系数，此三角形称为“杨辉三角”.根据“杨辉三角”提供的展开式的各项系数的规律，探究(a+b)20的展开式中第三项的系数为( )

A.2017B.2016C.191D.190
二、填空题

计算25的结果是________．

计算1m−1−2m2−1=_________.

在一个不透明的袋中装有5个小球，分别为2个红球和3个黑球，它们除颜色外无其他差别．随机摸出两个小球，则摸出两个颜色不同的小球的概率为________．

如图，在△ABC中，AB=AC，D为BC上一点，且BD=AB，AD=CD，求∠BAC的度数是__________．


如图，直线y=−x+6与反比例函数y=kxk>0,x>0的图象交于A、B两点，将该函数的图象平移得到的曲线是函数y=k+2xxk>0,x>0的图象，点A、B的对应点是A′、B′．若图中阴影部分的面积为8，则k的值为________.


如图，M，N分别是▱ABCD边BC，CD的中点，若∠MAN=∠B，则AMAB的值为________.

三、解答题

计算：3a2⋅2a4−3a32+4a6.

如图，四边形ABCD中，E是AB上一点，F是BC上一点，G在BC的延长线上．若∠A+∠DCG=180∘，AB//CD，EF//AD，求证：EF//BC.


选好志愿者，支持军运会．武汉市某校团委组织了一次八年级600名学生参加的“武汉军运知多少”知识大赛．为了了解本次大赛的成绩，随机抽取了部分学生的成绩作为样本，按A，B，C，D四个等级进行统计，制成如下不完整的统计图．
（说明：A级80分−100分，B级70分−79分，C级60−69分，D级0分−59分）
根据所给信息，解答以下问题：
(1)在扇形统计图中，C对应的扇形的圆心角是________度；

(2)直接写出条形统计图B级的频数________；

(3)所抽取学生的足球运球测试成绩的中位数会落在________等级；

(4)若成绩达到A级的学生可以选为志愿者，请估计该校八年级600名学生中可以选为志愿者学生有多少人？

要求在下列问题中仅用无刻度的直尺作图．
如图，在下列10×12的网格中，横、纵坐标均为整数的点叫做格点．例如正方形ABCD的顶点A0,7,C5,2都是格点．

(1)找一个格点M，连接AM交边CD于F，使DF=FC，画出图形写出点M的坐标为________.

(2)找一个格点N，连接ON交边BC于E，使BE=13BC，画出图形写出点N的坐标为________.

(3)连接AE、EF得________△AEF.请按步骤完成作图，并写出△AEF的面积为________.

如图，△ABC内接于⊙O，AB=AC，BD为⊙O的直径，过点A作AE⊥BD于点E，延长BD交AC延长线于点F．

(1)若AE=4，AB=5，求⊙O的半径；

(2)若BD=2DF，求sin∠ACB的值．

如图，在平面直角坐标系中，点A(m,n)(m>0)在双曲线y=4x上，

(1)如图1，m=1,∠AOB=45∘，点B正好在y=4xx>0上，求B点坐标；

(2)如图2，线段OA绕O点旋转至OC，且C点正好落在y=4x上，Ca,b，试求m与a的数量关系．

在等边△ABC中，D，E分别是射线BC、AB上的点，∠ADE=60∘.
(1)求证：△ADE∽△ABD；

(2)点D在BC延长线上，延长AC交DE于M，
①如图2，若ABAD=34，求ABBE；
②如图3，点N在DE上，AD=DN，且AN交BD于点H，若BHDM=23，直接写出BEAB的值.

已知抛物线y=12x2−2mx−4m+4经过定点A．
(1)直接写出A点坐标；

(2)直线y=tt<6与抛物线交于B，C两点（B在C的左边），过点A作AD⊥BC于点D，是否存在t的值，使得对于任意的m，∠DAC=∠ABD恒成立，若存在，请求t的值；若不存在，请说明理由．

(3)如图，当m=1时，直线y=2x交对称轴于点E，在直线OE的右侧作∠EOP交抛物线于点P，使得tan∠EOP=12，已知x轴上有一个点M(t,0)，EM+PM是否存在最小值？若存在，求t的值；若不存在，请说明理由．
参考答案与试题解析
2019-2020学年湖北省武汉市某校初三（下）期中考试数学试卷
一、选择题
1.
【答案】
D
【考点】
倒数
【解析】
此题暂无解析
【解答】
解：−2的倒数是−12.
故选D.
2.
【答案】
B
【考点】
二次根式有意义的条件
【解析】
根据二次根式的性质，被开方数大于等于0时，二次根式有意义．即可求解．
【解答】
解：根据题意得x−5≥0，即x≥5．
故选B.
3.
【答案】
D
【考点】
必然事件
不可能事件
随机事件
【解析】
根据事件发生的可能性大小判断相应事件的类型即可．
【解答】
解：四边形的内角和为360∘，故A是不可能事件；
明天太阳一定从东方升起，故B是必然事件；
通常温度降到0∘C以下，纯净的水一定结冰，故C是必然事件；
不在同一直线上的三点可以画一个圆，故D是随机事件.
故选D.
4.
【答案】
C
【考点】
中心对称图形
轴对称图形
【解析】
此题暂无解析
【解答】
解：A，该图为轴对称图形，不是中心对称图形；
B，该图是轴对称图形，不是中心对称图形；
C，该图是中心对称图形；
D，该图是轴对称图形，不是中心对称图形.
故选C.
5.
【答案】
D
【考点】
简单几何体的三视图
【解析】
此题暂无解析
【解答】
解：观察图形可知，主视图有3列，从左到右每列小正方数形数目分别为2，2，1，
据此可得出图形，该几何体的主视图是：
故选D.
6.
【答案】
D
【考点】
众数
中位数
【解析】
此题暂无解析
【解答】
解：由题意2出现的次数最多，故2是众数．
且将数据按从大到小的顺序排列好，2处在中间位置，故2也是中位数.
故选D.
7.
【答案】
D
【考点】
二元一次方程组的应用——其他问题
由实际问题抽象出二元一次方程组
【解析】
根据题意可得等量关系：①9枚黄金的重量=11枚白银的重量；②（10枚白银的重量+1枚黄金的重量）−（1枚白银的重量+8枚黄金的重量）=13两，根据等量关系列出方程组即可．
【解答】
解：由题已设每枚黄金重x两，每枚白银重y两，则由题意得：
9x=11y，(10y+x)−(8x+y)=13.
故选D.
8.
【答案】
A
【考点】
二次函数图象上点的坐标特征
【解析】
根据二次函数的性质得到抛物线y=−(x−1)2+m的开口向下，有最大值为m，对称轴为直线x=1，设A(x1, y1)的对称点为A′(x0, y1)，从而求得x1+x0=2，由x1<12，得出1y1>y2．
【解答】
解：∵ y=−(x−1)2+m，
∴ a=−1<0，有最大值为m，
∴ 抛物线开口向下，
∵ 抛物线y=−(x−1)2+m对称轴为直线x=1，
设A(x1, y1)的对称点为A′(x0, y1)，
∴ x1+x02=1，
∴ x1+x0=2，
∵ x1+x2>2，且x1<1∴ 1∴ m>y1>y2．
故选A．
9.
【答案】
B
【考点】
切线的性质
含30度角的直角三角形
角平分线的性质
平行线的性质
平行线的判定
角的计算
【解析】
此题暂无解析
【解答】
解：如图，连接OD，
∵ AC与⊙O相切，
∴OD⊥AC，
∴∠ODA=90∘
∵OB=OD，
∴∠1=∠2，
∵ BD平分∠ABC，
∴∠2=∠3，
∴∠1=∠3，
∴OD//BC，
∴∠C=∠ODA=90∘，
∴∠ABC=180∘−∠A−∠C=180∘−30∘−90∘=60∘，
∴∠2=∠3=12∠ABC=30∘，
∴∠2=∠A，
∴BD=AD=23，
∴CD=12BD=12×23=3.
故选B.
10.
【答案】
D
【考点】
完全平方公式
【解析】
根据图形中的规律即可求出(a+b)20的展开式中第三项的系数；
【解答】
解：找规律发现(a+b)3的第三项系数为3=1+2；
(a+b)4的第三项系数为6=1+2+3；
(a+b)5的第三项系数为10=1+2+3+4；
不难发现(a+b)n的第三项系数为
1+2+3+...+(n−2)+(n−1)，
∴ (a+b)20第三项系数为1+2+3+...+19=190.
故选D.
二、填空题
【答案】
5
【考点】
算术平方根
【解析】
利用算术平方根定义判断即可．
【解答】
解：25=5.
故答案为：5.
【答案】
1m+1
【考点】
分式的化简求值
平方差公式
【解析】
此题暂无解析
【解答】
解：原式=1(m+1)(m−1)(m+1)−2(m+1)(m−1)
=m+1−2(m+1)(m−1)
=1m+1.
故答案为：1m+1.
【答案】
35
【考点】
等可能事件的概率
列表法与树状图法
【解析】
根据题意画出树状图，再根据树状图即可求得所有等可能的结果与两次取出的小球颜色相同的情况，然后根据概率公式求解．
【解答】
解：画树状图如下：
由树状图可知，共有20种等可能结果，其中摸出的小球颜色不同的有12种结果，
∴ 摸出两个颜色不同的小球的概率为1220=35.
故答案为：35.
【答案】
108​∘
【考点】
等腰三角形的判定与性质
【解析】
由AB=AC，AB=BD，得到AB=AC=BD，且AD=DC，利用等边对等角得到∠B=∠C=∠DAC，∠BAD=∠BDA，设∠B=∠C=∠DAC=x，由外角性质得到∠BAD=∠BDA=∠C+∠DAC=2x，在三角形ABC中，利用三角形的内角和定理列出关于x的方程，求出方程的解得到x的值，确定出∠BAD与∠DAC的度数，由∠BAD+∠DAC即可求出∠BAC的度数．
【解答】
解：∵ AB=AC=BD，AD=DC，
∴ ∠B=∠C=∠DAC，∠BAD=∠BDA，
设∠B=∠C=∠DAC=x，
则∠BAD=∠BDA=∠C+∠DAC=2x，
∵ ∠B+∠C+∠BAC=180∘，
即x+x+2x+x=180∘，解得x=36∘，
∴ ∠B=∠C=∠DAC=36∘，
∴ ∠BAD=∠BDA=72∘，
∴ ∠BAC=∠BAD+∠DAC=72∘+36∘=108∘．
故答案为：108​∘.
【答案】
5
【考点】
反比例函数系数k的几何意义
平移的性质
【解析】
利用平行四边形的面积公式得出M的值，进而利用反比例函数图象上点的性质得出k的值．
【解答】
解：设A(x1,6−x1)，B(x2,6−x2)，
y=k+2xx=kx+2，
即将y=kx图象向上平移2个单位长度得到y=k+2xx，
点A、B的对应点分别为A′、B′，图中阴影部分的面积为8，
则x2−x1=4，x2=x1+4，
∵ A，B在y=kx上，
∴ k=x1(6−x1)=x2(6−x2)=(x1+4)(6−x1−4)，
解得x1=1，
∴ A(1,5)，
∴ k=1×5=5.
故答案为：5.
【答案】
32
【考点】
相似三角形的性质
相似三角形的判定
平行四边形的性质
全等三角形的判定
全等三角形的性质
【解析】
本题考查了平行四边形的性质、全等三角形的性质和判定、相似三角形的判定和性质，解题关键是掌握这些性质和判定并能熟练运用.
【解答】
解：如图，延长AM与DC的延长线交于H，
∵ 四边形ABCD为平行四边形，
∴ AB=//CD，
∴ ∠H=∠BAM，
∵ ∠B=∠MAN，
∴ △ABM∼△HAN，
∴ ABHA=AMHN，
∵ M、N分别是▱ABCD边BC、CD的中点，
∴ BM=MC，CN=DN=12CD=12AB，
∵ ∠AMB=∠HMC，∠H=∠BAM，
∴ △ABM≅△HCM，
∴ HC=AB，AM=MH，
∴ AH=2AM，HN=32AB，
∴ AB2AM=AM32AB，
即3AB2=4AM2，
∴ AMAB=32.
故答案为：32.
三、解答题
【答案】
解：原式=6a6−9a6+4a6
=a6.
【考点】
整式的混合运算——化简求值
同底数幂的乘法
幂的乘方与积的乘方
【解析】
此题暂无解析
【解答】
解：原式=6a6−9a6+4a6
=a6.
【答案】
证明：∵ AB//CD，
∴ ∠B=∠DCG，
∵ ∠A+∠DCG=180​∘，
∴ ∠A+∠B=180​∘，
∴ AD//BC，
∵ EF//AD，
∴ EF//BC.
【考点】
平行线的判定与性质
【解析】
此题暂无解析
【解答】
证明：∵ AB//CD，
∴ ∠B=∠DCG，
∵ ∠A+∠DCG=180​∘，
∴ ∠A+∠B=180​∘，
∴ AD//BC，
∵ EF//AD，
∴ EF//BC.
【答案】
117
18
B
(4)440×600=60（人）
答：估计该校八年级600名学生中可以选为志愿者学生有60人.
【考点】
圆心角与圆周角的综合计算
中位数
频数与频率
条形统计图
扇形统计图
用样本估计总体
【解析】
（1）先根据B等级人数及其百分比求得总人数，总人数减去其他等级人数求得C等级人数，继而用360∘乘以C等级人数所占比例即可得；
（2）根据以上所求结果即可补全图形；
（3）根据中位数的定义求解可得；
（4）总人数乘以样本中A等级人数所占比例可得．
【解答】
解：(1)∵ 总人数为18÷45%=40人，
∴ C等级人数为40−(4+18+5)=13人，
则C对应的扇形的圆心角是360∘×1340=117∘.
故答案为：117.
(2)由条形统计图知，B级的频数是18.
故答案为：18.
(3)∵ 共有40个数据，其中位数是第20、21个数据的平均数，
而第20、21个数据均落在B等级，
∴ 所抽取学生的足球运球测试成绩的中位数会落在B等级.
故答案为：B.
(4)440×600=60（人）
答：估计该校八年级600名学生中可以选为志愿者学生有60人.
【答案】
(10,2)
(5，6)
12512
【考点】
三角形的面积
点的坐标
【解析】
此题暂无解析
【解答】
解：(1)∵ DF=FC,
∴ F为DC中点，
由题画图：
故点M的坐标为(10,2).
故答案为：(10,2).
(2)∵ BE=13BC，
∴ 由图知：
∴ 点N的坐标为：(5，6).
故答案为：(5，6).
(3)由(1)(2)知：
BE=13BC=53，CF=FD=52，
∴ S△AEF=S正方形ABCD−S△ABE−S△ECF−S△AFD
=25−256−256−254
=12512.
故答案为：12512.
【答案】
解：(1)连接OA，
∵ AE⊥BD，
∴ ∠AEB=∠AED=90∘，
在Rt△ABE中，
BE=AB2−AE2=3，
设OA=OB=r，
∴ OE=r−3，
在Rt△AEO中，
42+(r−3)2=r2，
16+r2−6r+9=r2，
6r=25，
r=256，
∴ ⊙O的半径是256.
(2)连接CD，
∵ AB=AC，
∴ OA⊥BC，
∵ BD是直径，
∴ ∠BCD=90∘，
∴ CD⊥BC，
∴ OA//CD，
设OA与BC交于点H，OH=a，
则CD=2a，
∵ BD=2DF，
∴ OD=DF，OA=4a，
∴ AH=3a，
由勾股定理得BH=15a，
∴ AB=26a，
∴ sin∠ACB=64.
【考点】
锐角三角函数的定义--与圆有关
圆的有关概念
勾股定理
平行线的性质
平行线的判定
【解析】
此题暂无解析
【解答】
解：(1)连接OA，
∵ AE⊥BD，
∴ ∠AEB=∠AED=90∘，
在Rt△ABE中，
BE=AB2−AE2=3，
设OA=OB=r，
∴ OE=r−3，
在Rt△AEO中，
42+(r−3)2=r2，
16+r2−6r+9=r2，
6r=25，
r=256，
∴ ⊙O的半径是256.
(2)连接CD，
∵ AB=AC，
∴ OA⊥BC，
∵ BD是直径，
∴ ∠BCD=90∘，
∴ CD⊥BC，
∴ OA//CD，
设OA与BC交于点H，OH=a，
则CD=2a，
∵ BD=2DF，
∴ OD=DF，OA=4a，
∴ AH=3a，
由勾股定理得BH=15a，
∴ AB=26a，
∴ sin∠ACB=64.
【答案】
解∶(1)易求A1,4，作AE⊥OA，交直线OB于点E，
由图易得E5,3，
∴ OE的解析式：y=35x,
y=35x，y=4x，
35x=4x，x=2315，
∴ B(2315,2515) .
(2)设A(m,4m) ，B⟨a,4a)，
∵ OA2=OB2，
∴ m2+16m2=a2+16a2，(m2−a2)(1−16m2a2)=0，
∵ m≠a，
∴ m+a=0或ma=4,ma=−4 .
【考点】
全等三角形的性质与判定
旋转的性质
反比例函数的性质
【解析】
此题暂无解析
【解答】
解∶(1)易求A1,4，作AE⊥OA，交直线OB于点E，
由图易得E5,3，
∴ OE的解析式：y=35x,
y=35x，y=4x，
35x=4x，x=2315，
∴ B(2315,2515) .
(2)设A(m,4m) ，B⟨a,4a)，
∵ OA2=OB2，
∴ m2+16m2=a2+16a2，(m2−a2)(1−16m2a2)=0，
∵ m≠a，
∴ m+a=0或ma=4,ma=−4 .
【答案】
(1)证明：∵ △ABC是等边三角形，
∴ ∠B=60∘，
又∠ADE=60∘，
∴ ∠B=∠ADE.
又∠EAD=∠DAB，
∴ △ADE∼△ABD.
(2)解：①∵ △ABC是等边三角形，
∴ ∠ABC=60∘，
又∠ADE=60∘，
∴ ∠ABC=∠ADE.
又∠DAE=∠BAD，
∴ △ADE∼△ABD，
∴ ADAB=AEAD=43，
设AD=4，
∴ AE=163，AB=3，
∴ ABAE=916，
∴ ABBE=97.
②∵ AD=DN，∠ADE=60∘，
∴ △ADN是等边三角形，
∴ ∠DAN=∠AND=∠ADN=60∘，
∴ ∠BAC=∠DAN=60∘，
即∠BAH+∠HAC=∠DAM+∠HAC，
∴ ∠BAH=∠DAM，
∵ ∠ABH=∠E+∠HDN=60∘，
∠ANM=∠E+∠BAH=60∘，
∴ ∠HDN=∠BAH，
∴ ∠DAM=∠HDN.
在△ADM和△DNH中，
∠DAM=∠HDN，AD=DN，∠ADM=∠HND=60∘，
∴ △ADM≅△DNH，
∴ AM=DH，DM=NH，AD=DN，
∴ BD−AM=BH，
∵ ∠AHB=∠DHN，∠ABH=∠HND=60∘，
∴ △ABH∼△DNH，
∴ ABDN=BHNH=BHDM=23，
∴ ABAD=23，
∵ ∠BAD=∠DAE，∠ABD=∠ADE=60∘，
∴ △ABD∼△ADE，
∴ ABAD=ADAE=23，
设AD=4，则AE=6，AB=83，
∴ BE=AE−AB=103，
∴ BEAB=54.
【考点】
相似三角形的性质
相似三角形的判定
等边三角形的性质
全等三角形的判定
全等三角形的性质
【解析】
此题暂无解析
【解答】
(1)证明：∵ △ABC是等边三角形，
∴ ∠B=60∘，
又∠ADE=60∘，
∴ ∠B=∠ADE.
又∠EAD=∠DAB，
∴ △ADE∼△ABD.
(2)解：①∵ △ABC是等边三角形，
∴ ∠ABC=60∘，
又∠ADE=60∘，
∴ ∠ABC=∠ADE.
又∠DAE=∠BAD，
∴ △ADE∼△ABD，
∴ ADAB=AEAD=43，
设AD=4，
∴ AE=163，AB=3，
∴ ABAE=916，
∴ ABBE=97.
②∵ AD=DN，∠ADE=60∘，
∴ △ADN是等边三角形，
∴ ∠DAN=∠AND=∠ADN=60∘，
∴ ∠BAC=∠DAN=60∘，
即∠BAH+∠HAC=∠DAM+∠HAC，
∴ ∠BAH=∠DAM，
∵ ∠ABH=∠E+∠HDN=60∘，
∠ANM=∠E+∠BAH=60∘，
∴ ∠HDN=∠BAH，
∴ ∠DAM=∠HDN.
在△ADM和△DNH中，
∠DAM=∠HDN，AD=DN，∠ADM=∠HND=60∘，
∴ △ADM≅△DNH，
∴ AM=DH，DM=NH，AD=DN，
∴ BD−AM=BH，
∵ ∠AHB=∠DHN，∠ABH=∠HND=60∘，
∴ △ABH∼△DNH，
∴ ABDN=BHNH=BHDM=23，
∴ ABAD=23，
∵ ∠BAD=∠DAE，∠ABD=∠ADE=60∘，
∴ △ABD∼△ADE，
∴ ABAD=ADAE=23，
设AD=4，则AE=6，AB=83，
∴ BE=AE−AB=103，
∴ BEAB=54.
【答案】
解：(1)由题可得y=12x2−m(2x+4)+4，
当2x+4=0，即x=−2时，
抛物线经过定点，
∴ 定点为(−2,6).
(2)连结AB，AC .
∵ ∠DAC=∠ABD，
∴ tan∠DAC=tan∠ABD，
∴ DADB=DCDA，
∴ AD2=BD⋅CD，
∴ (6−t)2=(xB+2)(xC+2)，
∵ yB=yC=t，
∴ 12x2−2mx−4m+4=t，
∴ 12x2−2mx−4m+4−t=0，
∴ xB+xC=4m，xBxC=−8m+8−2t，
∴ t2−12t+36=xBxC+2(xB+xC)+4 .
∴ t2−12t+36=8−2t−8m+8m+4，
∴ t2−12t+36=12−2t，
∴ t2−10t+24=0，
∴ t2−10t+25=1，
∴ (t−5)2=1，
∴ t1=6，t2=4，
∵ t<6，∴ t=4 ，
即t=4 .
(3)过E作关于x轴的对称点E′，
过E作EF⊥y轴于F，过E作EF⊥OE于E交OP于E，过G作GH⊥FE于H .
∵ m=1，∴ xE=2 .
∵ y=2x过点E，
∴ E(2,4)，
∵ tan∠EOP=12，
∴ GE=12OE .
∵ OE=22+42=25，∴ GE=5 .
∵ ∠OFE=∠OEG=∠H=90∘，
∴ △OEF∽△EGH，
∴ GH=12OF=2，HG=12EF=1，
∴ G(4,3)，∴ 直线OP:y=34x .
∵ y=12x−2x，
∴ P(112,338) .
∵ E′(2,−4)，
∴ 直线E′:y=6528x−12114 .
当y=0时，6528x=12114，
∴ x=24265 .
即t=24265 .
【考点】
二次函数y=ax^2+bx+c (a≠0)的图象和性质
相似三角形的性质与判定
锐角三角函数的定义
二次函数综合题
【解析】
.
.
.
【解答】
解：(1)由题可得y=12x2−m(2x+4)+4，
当2x+4=0，即x=−2时，
抛物线经过定点，
∴ 定点为(−2,6).
(2)连结AB，AC .
∵ ∠DAC=∠ABD，
∴ tan∠DAC=tan∠ABD，
∴ DADB=DCDA，
∴ AD2=BD⋅CD，
∴ (6−t)2=(xB+2)(xC+2)，
∵ yB=yC=t，
∴ 12x2−2mx−4m+4=t，
∴ 12x2−2mx−4m+4−t=0，
∴ xB+xC=4m，xBxC=−8m+8−2t，
∴ t2−12t+36=xBxC+2(xB+xC)+4 .
∴ t2−12t+36=8−2t−8m+8m+4，
∴ t2−12t+36=12−2t，
∴ t2−10t+24=0，
∴ t2−10t+25=1，
∴ (t−5)2=1，
∴ t1=6，t2=4，
∵ t<6，∴ t=4 ，
即t=4 .
(3)过E作关于x轴的对称点E′，
过E作EF⊥y轴于F，过E作EF⊥OE于E交OP于E，过G作GH⊥FE于H .
∵ m=1，∴ xE=2 .
∵ y=2x过点E，
∴ E(2,4)，
∵ tan∠EOP=12，
∴ GE=12OE .
∵ OE=22+42=25，∴ GE=5 .
∵ ∠OFE=∠OEG=∠H=90∘，
∴ △OEF∽△EGH，
∴ GH=12OF=2，HG=12EF=1，
∴ G(4,3)，∴ 直线OP:y=34x .
∵ y=12x−2x，
∴ P(112,338) .
∵ E′(2,−4)，
∴ 直线E′:y=6528x−12114 .
当y=0时，6528x=12114，
∴ x=24265 .
即t=24265 .阅读数量
1本
2本
3本
3本以上
人数（人）
10
18
13
4