湘教版九年级下册第1章 二次函数1.5 二次函数的应用图文ppt课件

这是一份湘教版九年级下册第1章 二次函数1.5 二次函数的应用图文ppt课件，共26页。PPT课件主要包含了知识驿站，挖金币，第3题，第4题，第1题，第2题等内容，欢迎下载使用。

二次函数的应用是九年级下册数学中的重要教学内容，它从具体问题入手，以实际问题为背景，通过实例巩固学生所学的知识。让学生通过现实生活中的一些问题，充分感受到应用性问题的的重要性。二次函数是单变量最优化问题的数学模型，如生活中涉及的求最大利润，最大面积等。这体现了数学的实用性，是理论与实践结合的集中体现。本节课主要研究实际中的最大利润问题。
掌握商品经济等问题中的相等关系的寻找方法，并会应用函数关系式求利润的最值；
师生交流互动，分析和解决实际问题，体验数学在实际中的应用性，提高数学思维能力。
培养学生的合作交流意识、探索精神以及正确面对困难，迎接挑战的坚强品质。
利用二次函数解决商品利润问题，会解函数的最值问题。
学会分析实际问题，建立函数模型。
PK活动：书中自有黄金屋
中国现代数学之父：华罗庚
中国第一位数学女博士：徐瑞云
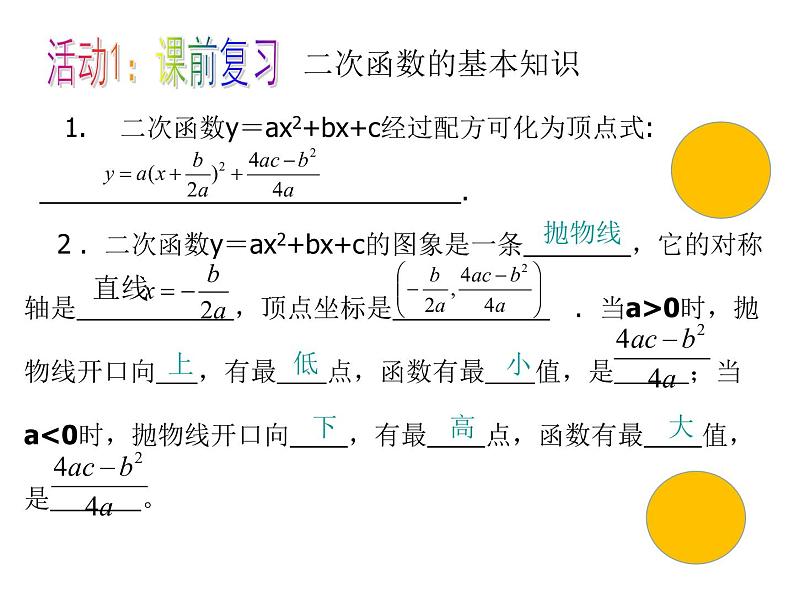
2 . 二次函数y＝ax2+bx+c的图象是一条 ，它的对称轴是 ，顶点坐标是 . 当a>0时，抛物线开口向 ，有最 点，函数有最 值，是 ；当 a<0时，抛物线开口向 ，有最 点，函数有最 值，是 。
1. 二次函数y＝ax2+bx+c经过配方可化为顶点式: .
除了前面讲的直观图象和运动中的抛物线问题，最大面积问题之外，在日常生活中存在着许许多多的与数学知识有关的实际问题。如繁华的商业城中很多人在买卖东西。
如果你去买商品，你会选买哪一家呢？如果你是商场经理，如何定价才能使商场获得最大利润呢？
1.5　二次函数的应用
第2课时　利用二次函数解决最大利润问题
（2）利润率＝ ×100%
利润问题的常用量及常用公式
（3）总利润＝ 利润×
（1）利润＝
问题1.已知某商品的进价为每件20元，售价是每件30元，每星期可卖出180件。市场调查反映：如果调整价格 ，每涨价1元，每星期要少卖出10件。要想获得最大的利润，该商品应定价为多少元？
请大家带着以下几个问题读题：
2、在涨价的情况下，如何确定利润与定价之间的关系？
1、题目中销售量随着价格是如何变化的？
3、你知道如何定价才能使利润最大吗？
销售单价上调了x元，那么每件商品的利润为 元，每周减少的销售量为 件 每周实际的销售量为 件，则一周的利润可表示为 元，
问题1.已知某商品的进价为每件20元，售价是每件30元，每星期可卖出180件。市场调查反映：如果调整价格 ，每涨价1元，每星期要少卖出10件。要想获得最大的利润，该商品应定价为多少元？
分析：没调价之前商场一周的总利润为 元；
设销售单价上调了x元，商场一周的总利润为y元；
y＝(10+x)( 180－10x)
确定一下x的取值范围应为：
问题1.已知某商品的进价为每件20元，售价是每件 30元，每星期可卖出180件。市场调查反映：如果调整价格 ，每涨价1元，每星期要少卖出10件。要想获得最大的利润，该商品应定价为多少元？
解：设销售单价上调了x元，一周的总利润为y元。
y＝(10+x)( 180－10x) （ 0≤x≤18）
y＝ －10x2+80x+1800
y＝ －10(x－4)2+1960
当x＝4时，即销售单价为34元时，y取最大值1960。
答：当销售单价为34元时，该店在一周内能获得最大利润1960元。
问题2.已知某民俗旅游村接待游客住宿，若每人每天收费x元与利润y元之间的关系式为：y＝－（x－15)²+100，因成本关系，收费定价范围为：20≤ x ≤25（x取整数）。那么每天最合适的收费是 元，利润为 元。
解：y＝－(x－15) 2 +100，可知抛物线对称轴为直线x＝15，开口向下，∴当x>15时，y随x的增大而减少。∵收费x的范围是20≤x≤15，x取整数。∴当x＝20时，y的值最大。即y＝－(20-15) 2 ＋100＝－25 ＋100＝75.∴x＝20时，y的最大值为75。
（1）列出二次函数的解析式，并根据自变量的实际意义，确定自变量的取值范围；（2）在自变量的取值范围内，运用公式法或通过配方求出二次函数的最大值或最小值。
利用二次函数解决利润问题时，根据利润公式等关系写出二次函数表达式是解决问题的关键。
课堂小结：本节课你学到了哪些知识?
1.谈谈这节课你的收获2.总结解这类最大利润问题的一般思路（1）列出二次函数的解析式，并根据自变量的实际意义，确定自变量的取值范围；（2）在自变量的取值范围内，运用公式法或通过配方求出二次函数的最大值或最小值。利用二次函数解决利润问题时，根据利润公式等关系写出二次函数表达式是解决问题的关键。
本节课我们进一步学习了用二次函数知识解决 最大利润问题，增强了应用数学知识的意识， 获得了利用数学方法解决实际问题的经验， 并进一步感受了数学建模思想和数学知识的 应用价值．
　 P32习题1.5A组　　 3
解：设旅行团人数为x人,营业额为y元。
1.某旅行社组团去外地旅游,30人起组团,每人单价80元.旅行社对超过30人的团给予优惠,即旅行团每增加一人,每人的单价就降低1元，直至免费。你能帮助分析一下,当旅行团的人数是多少时,旅行社可以获得最大营业额？
当x＝55时，y有最大值3025。即旅行团的人数是55人时，旅行社可以获得最大营业额3025元。
则：y＝x[80－﹙x－30﹚] ＝－x² + 110x ＝－(x－55)²+3025 ( 30≤x≤110 )
2.若某种商品的利润 y 元与售价 x （元）之间的函数关系式是 y ＝－ x 2 ＋ 8 x ＋ 9 ，且售价 x 的范围是 1 ≤ x ≤ 3 ，则最大利润是（　　）A. 16 元 B. 21 元 C. 24 元 D. 25 元
解：将y＝－x 2 ＋8x＋9配成顶点式为y＝－(x－4) 2 +25，可知抛物线对称轴为x＝4，开口向下，∴当x＜4时，y随x的增大而增大.∵售价x的范围是1≤x≤3，∴当x＝3时，y的值最大.即y＝－x 2 ＋8x＋9＝－3 2 ＋24＋9＝24.∴x＝3时，y的最大值为24.故选C.
3.出售某种文具盒，若每个获利x元，一天可售出(6－x)个，则当x＝_______元时，一天出售该种文具盒的总利润y最大。
解析：y＝x(6－x)＝－（x－3)²+9，所以当x ＝3时，获利最大