2022年中考数学复习之小题狂练450题（填空题）：投影与视图（含答案）

这是一份2022年中考数学复习之小题狂练450题（填空题）：投影与视图（含答案），共12页。试卷主要包含了时，液体的深度是 dm，是参加400m比赛时照的等内容，欢迎下载使用。
1．（2021•云南）如图图形是某几何体的三视图（其中主视图也称正视图，左视图也称侧视图）．已知主视图和左视图是两个全等的矩形．若主视图的相邻两边长分别为2和3，俯视图是直径等于2的圆，则这个几何体的体积为 ．

2．（2021•黔东南州模拟）由若干个小正方体组成的几何体的三视图如图所示，则组成这个几何体的小正方体的个数为 ．

3．（2021•扬州）如图是某圆柱体果罐，它的主视图是边长为10cm的正方形，该果罐侧面积为 cm2．

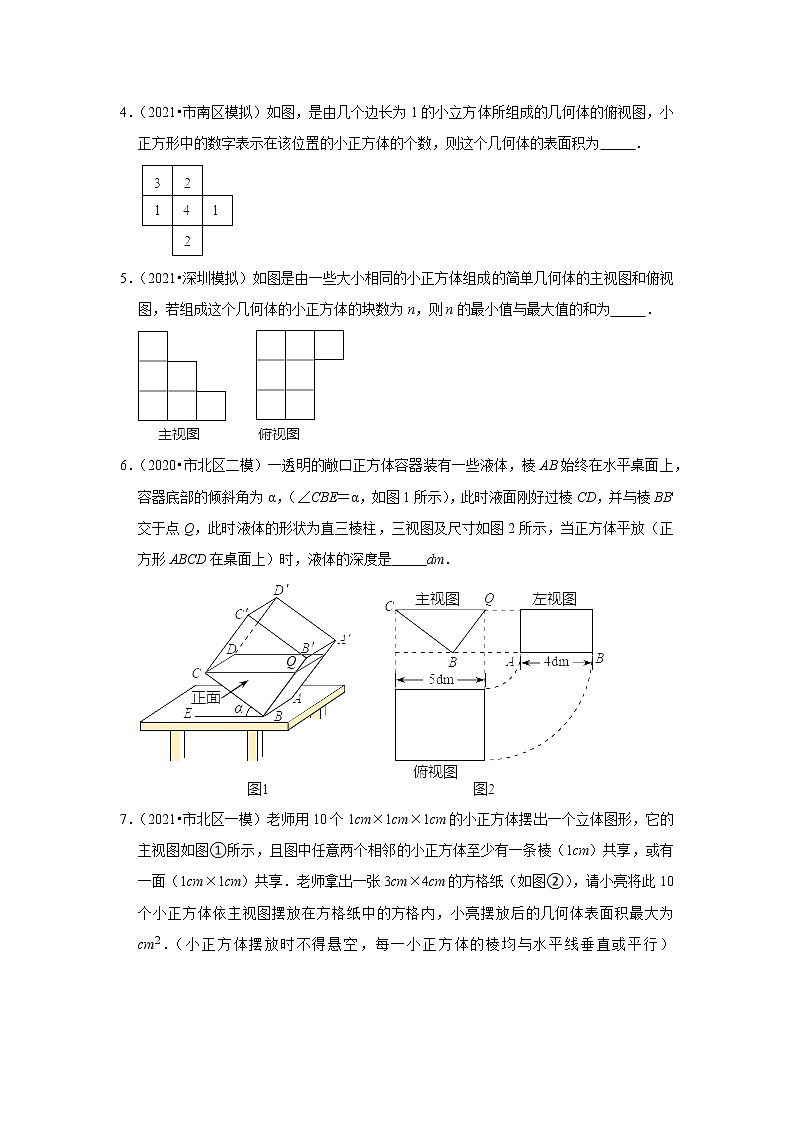
4．（2021•市南区模拟）如图，是由几个边长为1的小立方体所组成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，则这个几何体的表面积为 ．

5．（2021•深圳模拟）如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图，若组成这个几何体的小正方体的块数为n，则n的最小值与最大值的和为 ．

6．（2020•市北区二模）一透明的敞口正方体容器装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α，（∠CBE＝α，如图1所示），此时液面刚好过棱CD，并与棱BB'交于点Q，此时液体的形状为直三棱柱，三视图及尺寸如图2所示，当正方体平放（正方形ABCD在桌面上）时，液体的深度是 dm．

7．（2021•市北区一模）老师用10个1cm×1cm×1cm的小正方体摆出一个立体图形，它的主视图如图①所示，且图中任意两个相邻的小正方体至少有一条棱（1cm）共享，或有一面（1cm×1cm）共享．老师拿出一张3cm×4cm的方格纸（如图②），请小亮将此10个小正方体依主视图摆放在方格纸中的方格内，小亮摆放后的几何体表面积最大为 cm2．（小正方体摆放时不得悬空，每一小正方体的棱均与水平线垂直或平行）
8．（2020秋•白银期末）如图所示的是三个直立在地面上的艺术字母的投影（阴影部分）效果，在艺术字母“L，K，C”的投影中，属于同一种投影是 ．

9．（2021秋•晋中期末）皮影戏是一种以兽皮或纸板做成的人物剪影，在灯光照射下用隔亮布进行表演的民间戏剧．表演者在幕后操纵剪影、演唱，或配以音乐，具有浓厚的乡土气息．“皮影戏”中的皮影是 （填写“平行投影”或“中心投影”）．

10．（2021秋•紫金县月考）一天上午小红先参加了校运动会女子100m比赛，过一段时间又参加了女子400m比赛，如图是摄影师在同一位置拍摄的两张照片，那么 （填“甲”或“乙”照片）是参加400m比赛时照的．

2022年中考数学复习之小题狂练450题（填空题）：投影与视图（10题）
参考答案与试题解析
一．填空题（共10小题）
1．（2021•云南）如图图形是某几何体的三视图（其中主视图也称正视图，左视图也称侧视图）．已知主视图和左视图是两个全等的矩形．若主视图的相邻两边长分别为2和3，俯视图是直径等于2的圆，则这个几何体的体积为 3π ．

【考点】由三视图判断几何体；简单几何体的三视图．
【专题】投影与视图；运算能力．
【分析】由三视图得此几何体为：圆柱，并得到圆柱的底面半径和高，由体积公式计算出几何体的体积．
【解答】解：由三视图知几何体为圆柱，
且底面圆的半径是1，高是3，
∴这个几何体的体积为：π×12×3＝3π．
故答案为：3π．
【点评】本题考查由三视图求体积，解题的关键是熟练掌握三视图的作图规则，由三视图还原出实物图的几何特征．
2．（2021•黔东南州模拟）由若干个小正方体组成的几何体的三视图如图所示，则组成这个几何体的小正方体的个数为 6 ．

【考点】由三视图判断几何体．
【专题】投影与视图；空间观念．
【分析】根据三视图，该几何体的主视图以及俯视图可确定该几何体共有两层2列，故可得出该几何体的小正方体的个数．
【解答】解：综合三视图，我们可得出：

所以组成这个几何体的小正方体的个数为2+1+1+2＝6，
故答案为：6．
【点评】本题考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就容易得到答案．
3．（2021•扬州）如图是某圆柱体果罐，它的主视图是边长为10cm的正方形，该果罐侧面积为 100π cm2．

【考点】几何体的表面积；圆柱的计算；简单几何体的三视图；由三视图判断几何体．
【专题】投影与视图；空间观念．
【分析】此几何体为圆柱，那么侧面积＝底面周长×高．
【解答】解：由题意得圆柱的底面直径为10cm，高为10cm，
∴侧面积＝10π×10＝100π(cm2)．
故答案为：100π．
【点评】本题考查了由三视图判断几何体，难点是确定几何体的形状，关键是找到等量关系里相应的量．
4．（2021•市南区模拟）如图，是由几个边长为1的小立方体所组成的几何体的俯视图，小正方形中的数字表示在该位置的小正方体的个数，则这个几何体的表面积为 46 ．

【考点】几何体的表面积；由三视图判断几何体．
【专题】投影与视图；空间观念．
【分析】根据俯视图得出主视图、左视图的正方形的数目，表面积为三种视图的面积和的2倍．
【解答】解：这个几何体的主视图有三列，从左到右分别是3，4，1，左视图有三列，从左到右分别是3，4，2，
表面积为：（8+9+6）×2＝46，
故答案为：46．
【点评】考查简单几何体的三视图的画法，主视图、左视图、俯视图实际上就是从正面、左面、上面对该几何体正投影所得到的图形．画三视图时还要注意“长对正、宽相等、高平齐”．
5．（2021•深圳模拟）如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图，若组成这个几何体的小正方体的块数为n，则n的最小值与最大值的和为 26 ．

【考点】由三视图判断几何体．
【专题】投影与视图；空间观念．
【分析】根据主视图、俯视图，求出摆放最多时和最少时的正方体的个数，进而求出答案．
【解答】解：根据主视图、俯视图，可以得出最少时、最多时，在俯视图的相应位置上所摆放的个数如下：

最少时需要10个，最多时需要16个，
因此n＝10+16＝26，
故答案为：26．
【点评】本题考查简单组合体的三视图，在俯视图上相应位置标出所摆放的个数是解决问题的关键．
6．（2020•市北区二模）一透明的敞口正方体容器装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α，（∠CBE＝α，如图1所示），此时液面刚好过棱CD，并与棱BB'交于点Q，此时液体的形状为直三棱柱，三视图及尺寸如图2所示，当正方体平放（正方形ABCD在桌面上）时，液体的深度是 1.5 dm．

【考点】由三视图判断几何体．
【专题】投影与视图；空间观念．
【分析】首先根据水面与水平面平行可以得到CQ与BE平行，利用勾股定理即可求得BQ的长，由题意可知液体正好是一个以△BCQ是底面的直棱柱，据此即可求得液体的体积，进一步求得液体的深度．
【解答】解：∵CQ＝5dm，BC＝4dm，
∴BQ＝＝＝3（dm），
∴液体的体积为：V液＝×3×4×4＝24（dm3），
∴液体的深度是24÷（4×4）＝1.5（dm）．
故答案为：1.5．
【点评】本题考查了四边形的体积计算以及三视图的认识和勾股定理的运用，正确理解棱柱的体积的计算是关键．
7．（2021•市北区一模）老师用10个1cm×1cm×1cm的小正方体摆出一个立体图形，它的主视图如图①所示，且图中任意两个相邻的小正方体至少有一条棱（1cm）共享，或有一面（1cm×1cm）共享．老师拿出一张3cm×4cm的方格纸（如图②），请小亮将此10个小正方体依主视图摆放在方格纸中的方格内，小亮摆放后的几何体表面积最大为 52 cm2．（小正方体摆放时不得悬空，每一小正方体的棱均与水平线垂直或平行）
【考点】几何体的表面积；由三视图判断几何体．
【专题】投影与视图；应用意识．
【分析】如图，10个小正方体像俯视图中这样摆放时，几何体的表面积最大．
【解答】解：如图，10个小正方体像俯视图中这样摆放时，几何体的表面积最大，

最大值＝3×6+2×10+14＝52（cm2），
故答案为：52．
【点评】本题考查三视图，几何体的表面积等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
8．（2020秋•白银期末）如图所示的是三个直立在地面上的艺术字母的投影（阴影部分）效果，在艺术字母“L，K，C”的投影中，属于同一种投影是 L、K ．

【考点】平行投影．
【专题】投影与视图；空间观念．
【分析】通过判断光线是否平行确定中心投影和平移投影．
【解答】解：根据题意，字母L、K的投影为中心投影，字母C的投影为平行投影．
故答案为L、K．
【点评】本题考查了平行投影：由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影．平行投影中物体与投影面平行时的投影是全等的．也考查了中心投影．
9．（2021秋•晋中期末）皮影戏是一种以兽皮或纸板做成的人物剪影，在灯光照射下用隔亮布进行表演的民间戏剧．表演者在幕后操纵剪影、演唱，或配以音乐，具有浓厚的乡土气息．“皮影戏”中的皮影是 中心投影 （填写“平行投影”或“中心投影”）．

【考点】平行投影；中心投影．
【专题】投影与视图．
【分析】根据中心投影的定义判断即可．
【解答】解：“皮影戏”中的皮影是中心投影，
故答案为：中心投影．
【点评】本题考查中心投影，平行投影等知识，解题的关键是理解中心投影，平行投影的定义，属于中考常考题型．
10．（2021秋•紫金县月考）一天上午小红先参加了校运动会女子100m比赛，过一段时间又参加了女子400m比赛，如图是摄影师在同一位置拍摄的两张照片，那么 乙 （填“甲”或“乙”照片）是参加400m比赛时照的．

【考点】平行投影．
【分析】在不同时刻，同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变，方向也在改变，依此进行分析．
【解答】解：根据平行投影的规律：从早晨到傍晚物体的指向是：西﹣西北﹣北﹣东北﹣东，影长由长变短，再变长；
∵比赛是在上午进行，
∴则甲照片是参加100m的，乙照片是参加400m的．
故答案为：乙．
【点评】本题考查平行投影的特点和规律．在不同时刻，同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变，方向也在改变，就北半球而言，从早晨到傍晚物体的指向是：西﹣西北﹣北﹣东北﹣东，影长由长变短，再变长．
考点卡片
1．几何体的表面积
（1）几何体的表面积＝侧面积+底面积（上、下底的面积和）
（2）常见的几种几何体的表面积的计算公式
①圆柱体表面积：2πR2+2πRh （R为圆柱体上下底圆半径，h为圆柱体高）
②圆锥体表面积：πr2+nπ（h2+r2）360（r为圆锥体低圆半径，h为其高，n为圆锥侧面展开图中扇形的圆心角）
③长方体表面积：2（ab+ah+bh） （a为长方体的长，b为长方体的宽，h为长方体的高）
④正方体表面积：6a2 （a为正方体棱长）
2．圆柱的计算
（1）圆柱的母线（高）等于展开后所得矩形的宽，圆柱的底面周长等于矩形的长．
（2）圆柱的侧面积＝底面圆的周长×高
（3）圆柱的表面积＝上下底面面积+侧面积
（4）圆柱的体积＝底面积×高．
3．简单几何体的三视图
（1）画物体的主视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．
（2）常见的几何体的三视图：

圆柱的三视图：
4．由三视图判断几何体
（1）由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．
（2）由物体的三视图想象几何体的形状是有一定难度的，可以从以下途径进行分析：
①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高；
②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线；
③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助；
④利用由三视图画几何体与有几何体画三视图的互逆过程，反复练习，不断总结方法．
5．平行投影
（1）物体在光线的照射下，会在地面或墙壁上留下它的影子，这就是投影现象．一般地，用光线照射物体，在某个平面（底面，墙壁等）上得到的影子叫做物体的投影，照射光线叫做投影线，投影所在的平面叫做投影面．
（2）平行投影：由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影．
（3）平行投影中物体与投影面平行时的投影是全等的．
（4）判断投影是平行投影的方法是看光线是否是平行的．如果光线是平行的，所得到的投影就是平行投影．
（5）正投影：在平行投影中，投影线垂直于投影面产生的投影叫做正投影．
6．中心投影
（1）中心投影：由同一点（点光源）发出的光线形成的投影叫做中心投影．如物体在灯光的照射下形成的影子就是中心投影．
（2）中心投影的光线特点是从一点出发的投射线．物体与投影面平行时的投影是放大（即位似变换）的关系．
（3）判断投影是中心投影的方法是看光线是否相交于一点，如果光线是相交于一点，那么所得到的投影就是中心投影．