
初中数学人教版八年级下册第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教案
展开《18.1.3平行四边形判定定理的简单应用》导学案
一、 动手发现,合作交流
小组合作:
你能用:(1)两块全等的三角形纸板;(2)两根等长的小棒;(3)两条不等长的毛线;(4)一支粉笔,这4组物品,结合你对平行四边形判定的认识,构造出平行四边形吗?说说你的方法和依据。开动脑筋,尝试一下吧!
方案一:
方案二:
方案三:
方案四:
二、 探究发现,得出方法
探究1、已知平行四边形ABCD中,E、F分别是边AD、BC的中点,连接BE,DF.
求证:四边形BEDF是平行四边形.
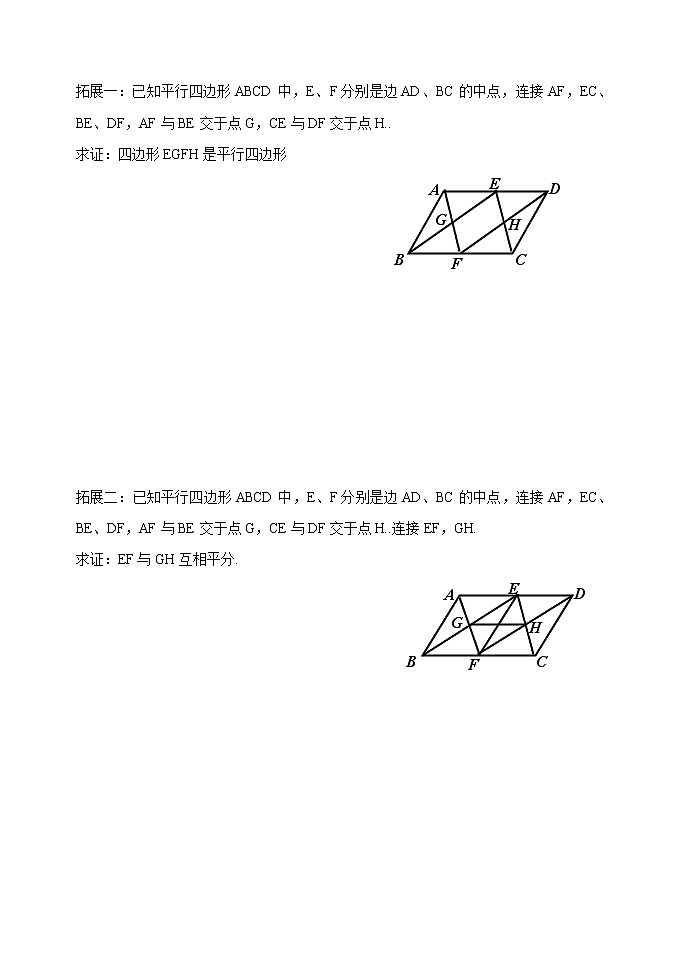
拓展一:已知平行四边形ABCD中,E、F分别是边AD、BC的中点,连接AF,EC、BE、DF,AF与BE交于点G,CE与DF交于点H..
求证:四边形EGFH是平行四边形
拓展二:已知平行四边形ABCD中,E、F分别是边AD、BC的中点,连接AF,EC、BE、DF,AF与BE交于点G,CE与DF交于点H..连接EF,GH.
求证:EF与GH互相平分.
探究2、如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,A(4,0),B(7,0).将△ABC沿着x轴向左平移,当点A与原点重合时,求线段BC扫过的面积.
探究3、已知,在平面直角坐标中,O(0,0),A(-1,1),B(2,2).
问:是否存在点C,使以O、A、B、C为顶点的四边形是平行四边形?
如果存在,求出点C坐标;如果不存在,请说明理由.
三、 归纳总结,提升认识
结合上面的探究问题,谈一谈:平行四边形判定定理有哪些简单应用?举例说明。
四、 作业布置,巩固认识
1、如图,□ABCD的对角线AC、BD相交于点O, E、F
分别是OD,OB的中点. 求证:AE=CF .
2、已知,在平面直角坐标中有三个点:A(1,0),B(4,0)C(2,3).
是否存在点D,使以A、B、C 、D为顶点的四边形是平行四边形?
如果存在,请写出所有满足条件的点D的坐标,并求出相应的平行四边形的面积;如果不存在,请说明理由.
3、(提高题)在四边形ABCD中,AD∥BC,AB⊥AD, AD=12cm,BC=21cm,,点P从点A以1cm/s的速度向点D运动,同时点Q从点C以1.5cm/s的速度向点B运动.设运动时间为t秒.问当t为何值时,以P、D、C、Q为顶点的四边形是平行四边形?
初中人教版第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教案及反思: 这是一份初中人教版第十八章 平行四边形18.1 平行四边形18.1.2 平行四边形的判定教案及反思,共2页。教案主要包含了本节课比较顺利完成教学目标,本节课的亮点,本节课的不足等内容,欢迎下载使用。
初中数学人教版八年级下册18.1.2 平行四边形的判定教学设计: 这是一份初中数学人教版八年级下册18.1.2 平行四边形的判定教学设计,共2页。教案主要包含了学习目标等内容,欢迎下载使用。
初中数学18.1.2 平行四边形的判定教案: 这是一份初中数学18.1.2 平行四边形的判定教案,共4页。教案主要包含了教学目标,重点,学情分析,教学过程设计,回顾小结,课后作业,板书设计等内容,欢迎下载使用。













