第07章 一元二次方程-2021年中考数学一轮复习（考点梳理＋重难点讲解＋过关演练）（通用版）（含答案）

这是一份第07章 一元二次方程-2021年中考数学一轮复习（考点梳理＋重难点讲解＋过关演练）（通用版）（含答案），共14页。

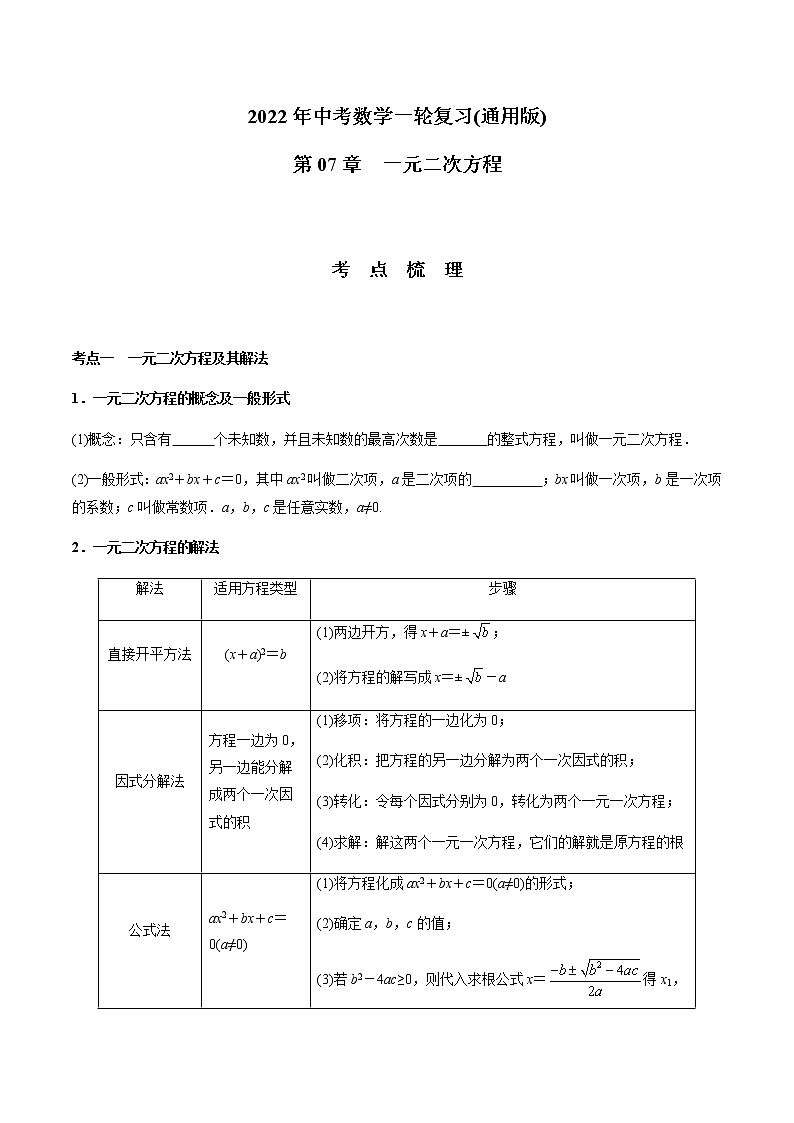
2022年中考数学一轮复习(通用版)
第07章 一元二次方程

考 点 梳 理

考点一 一元二次方程及其解法
1．一元二次方程的概念及一般形式
(1)概念：只含有 个未知数，并且未知数的最高次数是 的整式方程，叫做一元二次方程．
(2)一般形式：ax2＋bx＋c＝0，其中ax2叫做二次项，a是二次项的 ；bx叫做一次项，b是一次项的系数；c叫做常数项．a，b，c是任意实数，a≠0.
2．一元二次方程的解法
解法
适用方程类型
步骤
直接开平方法
(x＋a)2＝b
(1)两边开方，得x＋a＝±；
(2)将方程的解写成x＝±－a
因式分解法
方程一边为0，另一边能分解成两个一次因式的积
(1)移项：将方程的一边化为0；
(2)化积：把方程的另一边分解为两个一次因式的积；
(3)转化：令每个因式分别为0，转化为两个一元一次方程；
(4)求解：解这两个一元一次方程，它们的解就是原方程的根
公式法
ax2＋bx＋c＝0(a≠0)
(1)将方程化成ax2＋bx＋c＝0(a≠0)的形式；
(2)确定a，b，c的值；
(3)若b2－4ac≥0，则代入求根公式x＝得x1，x2；若b2－4ac<0，则方程无实数根
配方法
x2＋px＋q＝0(p为偶数)
(1)若二次项系数不为1，先把系数化为1再配方；
(2)把常数项移到方程的另一边，即x2＋px＝－q；
(3)在方程两边同时加上一次项系数一半的平方，即x2＋px＋()2＝－q＋()2；
(4)把方程整理成(x＋)2＝－q＋()2的形式；
(5)运用直接开平方法解方程
【点拨】解一元二次方程的注意事项：(1)在运用公式法解一元二次方程时，要先把方程化为一般形式，再确定a，b，c的值，否则易出现符号错误； (2)用因式分解法解一元二次方程时，一定要保证等号的右边化为0，否则易出现错误；(3)如果一元二次方程的常数项为0，不能在方程两边同时除以未知数，否则会漏掉x＝0的情况；(4)对于含有不确定量的方程，需要把求出的解代入原方程检验，避免增根．

考点二 一元二次方程根的判别式及根与系数的关系
1. 根的判别式
b2－4ac叫做一元二次方程ax2＋bx＋c＝0(a≠0)的根的判别式，通常用符号“Δ”来表示，即Δ＝ .
(1)Δ>0时，方程有 的实数根；
(2)Δ＝0时，方程有 的实数根；
(3)Δ<0时，方程 实数根．
【点拨】一元二次方程根的判别式的注意事项：(1)若二次项系数含字母，要注意判别二次项系数不为0；(2)注意题设中的隐含条件：方程有两个实数根隐含为一元二次方程二次项系数不为0；方程有实数根①方程是一次方程；②方程是二次方程，且有实数根.
2. 根与系数的关系
如果方程ax2＋bx＋c＝0(a≠0)的两个根为x1，x2，那么x1＋x2＝ ，x1x2＝ ．

考点三 一元二次方程的应用
1．列一元二次方程解应用题的一般步骤：审、设、列、解、验、答．
2．常考类型及其关系式
(1)变化率问题：设a是基础量，x为平均增长率，2为增长次数，b为增长后的量，则a(1＋x)2＝b，当x为平均下降率，2为下降次数，b为下降后的量时，则a(1－x)2＝b.
(2)面积问题：如图1，设空白部分的宽为x，则S阴影＝(a－2x)(b－2x)．

如图2、图3、图4，设阴影道路的路口宽为x，则S空白＝(a－x)(b－x)．

如图5，栏杆总长为a，BC的长为b，则S阴影＝.
(3)销售利润问题：毛利润＝售出总额－进货总额；
纯利润＝售出总额－进货总额－其他费用；
利润率＝利润÷成本×100%；
售出总额＝售价×销量；
进货总额＝进价×进货数量．
(4)握手、单循环赛与送礼物问题：握手、单循环赛总次数为(n为人数或场数)；送礼物总份数为n(n－1)(n为人数)．
【点拨】通常情况下一元二次方程有两个实数根，所以解一元二次方程的应用题时一定要验根，检验结果是否符合实际问题或是否满足题目中隐含的条件.





重 难 点 讲 解

考点一 一元二次方程的解法
方法指导：
理解各种解法的适用类型，在解一元二次方程时，首选因式分解法，次选配方法，当这两种方法都不适用时，再采用公式法．常见以下四种情形及应对策略：
(1)对于形如(x－a)2＝b(b≥0)的方程可以用直接开平方法求解；
(2)对于ax2＋bx＋c＝0(a≠0)，当b为偶数又不能分解因式的可以用配方法较快解出；
(3)对于ax2＋bx＋c＝0(a≠0)，当b为奇数又不能分解因式的可用公式法；
(4)能分解因式的就用因式分解法．
经典例题1 (2020•安徽模拟)解方程：3x2－5x＋1＝0.
【解析】 观察方程特点，可以考虑利用求根公式解答．
解：∵a=3，b=－5，c=1.
∴b2－4ac=(－5)2－4×3×1=13＞0.
∴由求根公式得x＝＝，
即x1＝，x2＝．

考点二 一元二次方程根的判别式及根与系数的关系
方法指导：
运用根的判别式时的注意事项：(1)根的判别式适用于一元二次方程，所以根据根的情况，求方程中字母的取值范围时要注意保证二次项系数不为0.(2)不解方程，使用判别式判断方程根的情况时，一定要先把方程法为一般形式才能准确确定a，b，c的值；(3)如果方程有实数根，那么包括有两个不相等的实数根和有两个相等实数两种情况切无遗漏；(4)“方程有实数根”与“一元二次方程有实数根”是两个不同概念.“方程有实根”中的方程，可以是一元二次方程，也可以是一元一次方程.
经典例题2 (2020•广东广州一模)关于x的一元二次方程4x2－ax－50＝0，下列结论一定正确的是(　 　)
A．该方程没有实数根 B．该方程有两个不相等的实数根
C．该方程有两个相等的实数根 D．无法确定
【解析】 ∵△＝(－a)2－4×4×(－50)＝a2＋800＞0，∴该方程有两个不相等的实数根．
【答案】 B

考点三 一元二次方程的实际应用
方法指导：
掌握列一元二次方程解应用题的一般步骤
(1)审：是指读懂题目，弄清题意，明确哪些是已知量，哪些是未知量以及它们之间的等量关系．
(2)设：是指设未知数．
(3)列：就是列方程，这是非常重要的步骤，一般先找出能够表达应用题全部含义的一个等量关系，然后列代数式表示等量关系中的各个量，就得到含有未知数的等式，即方程．
(4)解：就是解方程，求出未知数的值．
(5)验：是指检验方程的解能否保证实际问题有意义，符合题意．
(6)答：就是写出答案．
经典例题3 (2020•黑龙江大庆一模)某汽车公司今年8月份销售6000辆汽车，10月份销售汽车数量比8月份多615辆．求该公司9月份、10月份销售汽车数量的月平均增长率．
【解析】 设该公司9月份、10月份销售汽车数量的月平均增长率为x，根据该公司今年8月份及10月份销售汽车的数量，即可得出关于x的一元二次方程，解之取其正值即可得出结论．
解：设该公司9月份、10月份销售汽车数量的月平均增长率为x，
依题意，得6000(1＋x)2＝6000＋615，
解得x1＝＝5%，x2＝－(不合题意，舍去)．
答：该公司9月份、10月份销售汽车数量的月平均增长率为5%．







过 关 演 练

1．(2020·江西模拟)下列方程中，一定是一元二次方程的是(　　)
A．2x＋3y－6＝0 B．2x2＝0
C．(m＋1)x2＋3x＋1＝0 D．x2－x(x－1)＋4＝0
2．(2020•江苏泰安)将一元二次方程x2－8x－5＝0化成(x＋a)2＝b(a，b为常数)的形式，则a，b的值分别是(　　)
A．－4，21 B．－4，11 C．4，21 D．－8，69
3．(2020•四川凉山州)一元二次方程x2＝2x的根为(　　)
A．x＝0 B．x＝2 C．x＝0或x＝2 D．x＝0或x＝－2
4．(2020·青海模拟)关于x的一元二次方程(a＋1)x2－2x＋2＝0没有实数根，整数a的最小值为(　　)
A．－ B．－1 C．－2 D．0
5．(2020•四川自贡)关于x的一元二次方程ax2－2x＋2＝0有两个相等实数根，则a的值为(　　)
A． B．－ C．1 D．－1
6．(2020•贵州黔东南州)已知关于x的一元二次方程x2＋5x－m＝0的一个根是2，则另一个根是(　　)
A．－7 B．7 C．3 D．－3
7．(2020·江苏无锡模拟)制造一种产品，原来的成本是每件200元，由于连续两次降低成本，现在每件产品的成本是162元，则平均每次降低成本(　　)
A．8%　　　　　　　 B．10% C．15% D．20%
8．(2020•浙江衢州)某厂家2020年1～5月份的口罩产量统计如图所示．设从2月份到4月份，该厂家口罩产量的平均月增长率为x，根据题意可得方程(　　)

A．180(1－x)2＝461 B．180(1＋x)2＝461
C．368(1－x)2＝442 D．368(1＋x)2＝442
9．(2020•安徽一模)某地区2017年投入教育经费2500万元，预计2019年投入3600万元．则这两年投入教育经费的年平均增长率为(　　)
A．10% B．20% C．25% D．40%
10．(2020·吉林模拟)若关于x的一元二次方程x2－4x＋m＋2＝0有两个不相等实数根，且m为正整数，则此方程的解为(　　)
A．x1＝－1，x2＝3 B．x1＝－1，x2＝－3
C．x1＝1，x2＝3 D．x1＝1，x2＝－3
11．(2020•安徽阜阳一模)用公式法解一元二次方程，得x＝，则该一元二次方程是　 　．
12．(2020•上海中考)如果关于x的方程x2－4x＋m＝0有两个相等的实数根，那么m的值是　 　．
13．(2020•江苏泰州)方程x2＋2x－3＝0的两根为x1，x2，则x1•x2的值为　 　．
14．(2020•四川甘孜州)三角形的两边长分别为4和7，第三边的长是方程x2－8x＋12＝0的解，则这个三角形的周长是　 　．
15．(2020•贵州黔西南州)有一人患了流感，经过两轮传染后，共有121人患了流感，每轮传染中平均每人传染了　 　个人．
16．(2020•安徽合肥模拟)已知a－b＝2，ab＋2b－c2＋2c＝0，当b≥0，－2≤c＜1时，整数a的值是　 　．
17. (2020•山西一模)解方程：(x－1)(x＋3)＝12．




18．(2020·江西模拟)解方程：－3x2＋6x＝1.




19. (2020•安徽宿州模拟)已知关于x的一元二次方程x2＋mx－6＝0．
(1)求证：不论m为何实数，方程总有两个不相等的实数根；
(2)若m＝1，用配方法解这个一元二次方程．





20．(2020·浙江宁波模拟)已知关于x的方程x2＋2kx＋k2－1＝0.
(1)试说明无论k取何值时，方程总有两个不相等的实数根．
(2)如果方程有一个根为3，试求2k2＋12k＋2020的值．




21．(2020·山东泰安模拟)已知关于x的一元二次方程x2－2x＋m－1＝0有两个不相等的实数根．
(1)求m的取值范围；
(2)如果m为非负整数，且该方程的根都是整数，求m的值．




22. (2020·陕西西安模拟)某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售，当此农产品售价为每袋36元时，3月份销售125袋，4、5月份该农产品十分畅销，销售量持续走高．在售价不变的基础上，5月份的销售量达到180袋．设4、5这两个月销售量的月平均增长率不变．
(1)求4、5这两个月销售量的月平均增长率；
(2)6月份起，该商店采用降价促销的方式回馈顾客，经调查发现，该农产品每袋降价1元，销量就增加4袋，当农产品每袋降价多少元时，该商店6月份获利1920元？





23. (2020·安徽安庆一模)读诗词解题：(通过列方程式，算出周瑜去世时的年龄)
大江东去浪淘尽，千古风流数人物；
而立之年督东吴，早逝英年两位数；
十位恰小个位三，个位平方与寿符；
哪位学子算得快，多少年华属周瑜？




24．(2020•上海)去年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%．
(1)求该商店去年“十一黄金周”这七天的总营业额；
(2)去年，该商店7月份的营业额为350万元，8、9月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与9月份的营业额相等．求该商店去年8、9月份营业额的月增长率．









参 考 答 案

考点梳理
考点一 1. (1)一 2次 (2)系数
考点二 1. b2－4ac (1)两个不相等 (2)两个相等 (3)没有 2. －

过关演练
1. B
2. A 解析：∵x2－8x－5＝0，∴x2－8x＝5，则x2－8x＋16＝5＋16，即(x－4)2＝21，∴a＝－4，b＝21.
3. C 解析：∵x2＝2x，∴x2－2x＝0，则x(x－2)＝0，∴x＝0或x－2＝0，解得x1＝0，x2＝2．
4. D 解析:∵关于x的一元二次方程(a＋1)x2－2x＋2＝0没有实数根，∴ 即(x－1)(x－3)＝0，解得a＞－∵a为整数，∴a的最小值为0.
5. A 解析：∵关于x的一元二次方程ax2－2x＋2＝0有两个相等实数根，∴ ∴a＝．
6. A 解析：设另一个根为x，则x＋2＝－5，解得x＝－7．
7. B
8. B 解析：从2月份到4月份，该厂家口罩产量的平均月增长率为x，根据题意可得方程：180(1＋x)2＝461．
9. B 解析：设增长率为x，根据题意得2500(1＋x)2＝3600，解得x1＝0.2＝20%，x2＝－2.2(舍去)．
10. C 解析：∵关于x的一元二次方程x2－4x＋m＋2＝0有两个不相等实数根，∴Δ＝(－4)2－4×1×(m＋2)＞0，解得m＜2，∵m为正整数，∴m＝1，则方程为x2－4x＋3＝0，即(x－1)(x－3)＝0，解得x1＝1，x2＝3.
11. 3x2＋5x＋1＝0 解析：根据求根公式确定方程. 根据题意可知a＝3，b＝5，c＝1，则该一元二次方程是3x2＋5x＋1＝0.
12. 4 解析：依题意，∵方程x2－4x＋m＝0有两个相等的实数根，∴△＝b2－4ac＝(－4)2－4m＝0，解得m＝4．
13. －3 解析：∵方程x2＋2x－3＝0的两根为x1，x2，∴x1•x2＝＝－3．
14. 17 解析：x2－8x＋12＝0，(x－2)(x－6)＝0，解得：x1＝2，x2＝6，若x＝2，即第三边为2，4＋2＝6＜
7，不能构成三角形，舍去；当x＝6时，这个三角形周长为4＋7＋6＝17．
15. 10 解析：设每轮传染中平均每人传染了x人．依题意，得1＋x＋x(1＋x)＝121，即(1＋x)2＝121，解方程，得x1＝10，x2＝－12(舍去)．故每轮传染中平均每人传染了10人．
16. 2或3 解析：由a－b＝2，得出a＝2＋b，进一步代入ab＋2b－c2＋2c＝0，进一步利用完全平方公式得到(b＋2)2－(c－1)2－3＝0，再根据已知条件得到b的值. ∵a－b＝2，∴a＝2＋b，∴ab＋2b－c2＋2c＝b(b＋2)＋2b－c2＋2c＝b2＋4b－(c2－2c)＝(b＋2)2－(c－1)2－3＝0，b≥0，－2≤c＜1，∴4≤(b＋2)2≤12，∴a是整数，∴b＝0或1，∴a＝2或3．
17. 解：原方程整理为x2＋2x－15＝0，
∴(x－3)(x＋5)＝0，
∴x－3＝0或x＋5＝0，
∴x1＝－5，x2＝3．
18. 解：－3x2＋6x＝1变形为－3x2＋6x－1＝0，b2－4ac＝62－4×(－3)×(－1)＝24，x＝，x1＝，x2＝.
19. (1)证明：△＝m2－4×1×(－6)＝m2＋24．∵m2≥0，∴m2＋24＞0，即△＞0，∴不论m为何实数，方程总有两个不相等的实数根；
(2)解：当m＝1时，原方程为x2＋x－6＝0，移项，得x2＋x＝6，配方，得x2＋2×x＋()2＝6＋()2，即(x＋)2＝()2，开方得x＋＝±，∴x1＝2，x2＝－3．
20. 解：(1)∵Δ＝(2k)2－4×1×(k2－1)＝4k2－4k2＋4＝4＞0，∴无论k取何值时，方程总有两个不相等的实数根．　
(2)因为方程有一个根为3，所以9＋6k＋k2－1＝0，即k2＋6k＝－8，所以2k2＋12k＋2020＝2(k2＋6k)＋2020＝－16＋2020＝2004.
21. 解：(1)根据题意得(－2)2－4(m－1)＞0，解得m＜2，故m的取值范围为m＜2.　(2)由(1)得m＜2，∵m为非负整数，∴m＝0或1，把m＝0代入原方程得x2－2x－1＝0，解得x1＝1－，x2＝1＋，∴m＝0不合题意舍去；把m＝1代入原方程得x2－2x＝0，解得x1＝0，x2＝2.故m的值是1.
22. 解：(1)设4、5这两个月销售量的月平均增长率为x，依题意，得125(1＋x)2＝180，解得x1＝0.2＝20%，x2＝－2.2(不合题意，舍去)．答：4、5这两个月销售量的平均增长率为20%.　
(2)设每袋降价y元，则6月份的销售量为(180＋4y)袋，依题意，得(36－y－23)(180＋4y)＝1920，解得y1＝3，y2＝－35(不合题意，舍去)．答：当农产品每袋降价3元时，该商店6月份获利1920元．
23. 解：设周瑜逝世时的年龄的个位数字为x，则十位数字为(x－3)．由题意得10(x－3)＋x＝x2，解得x1＝5，x2＝6，当x＝5时，周瑜的年龄25岁，非而立之年，不合题意，舍去；当x＝6时，周瑜年龄为36岁，符合题意．答：周瑜去世的年龄为36岁．
24. 解：(1)450＋450×12%＝504(万元)．答：该商店去年“十一黄金周”这七天的总营业额为504万元．
(2)设该商店去年8、9月份营业额的月增长率为x，依题意，得350(1＋x)2＝504，解得x1＝0.2＝20%，x2＝－2.2(不合题意，舍去)．答：该商店去年8、9月份营业额的月增长率为20%．