




所属成套资源:备战2021年中考数学临考题号押题(全国通用版)
专题04 平行线(选择题)-备战2021年中考数学临考题号押题(全国通用版)
展开
这是一份专题04 平行线(选择题)-备战2021年中考数学临考题号押题(全国通用版),文件包含专题04平行线选择题解析版doc、专题04平行线选择题原卷版doc等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
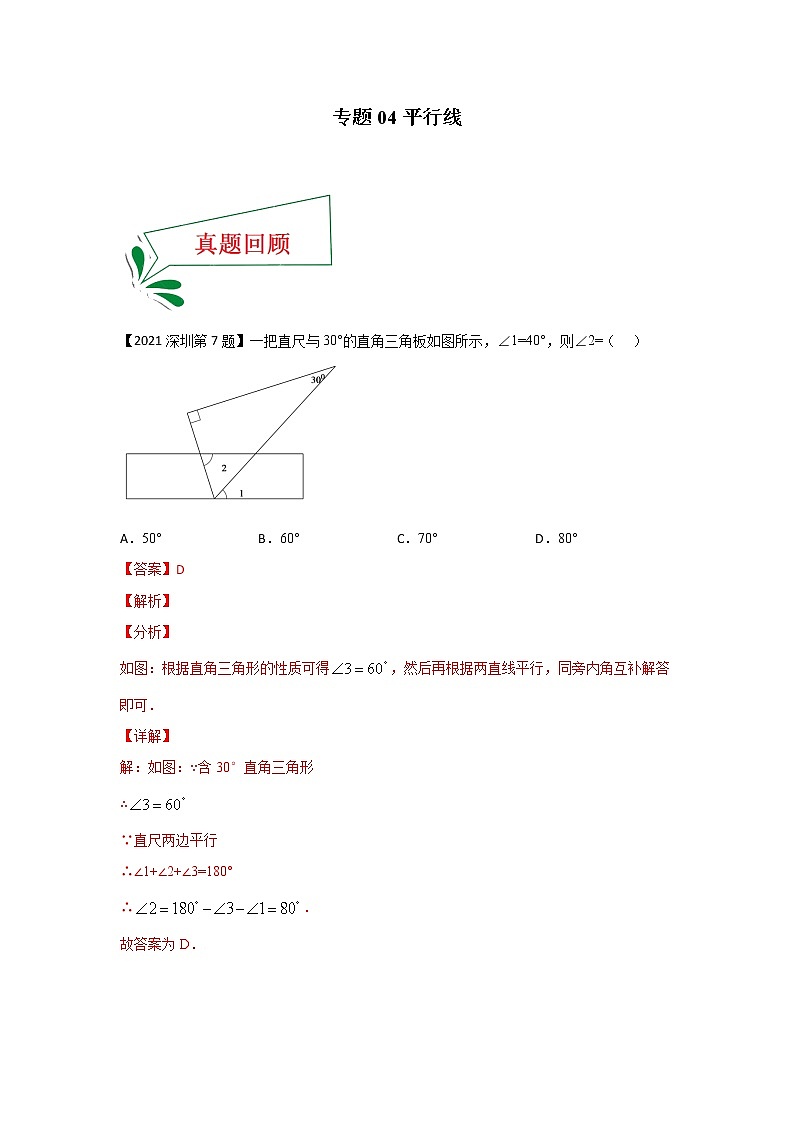
专题04平行线 【2021深圳第7题】一把直尺与30°的直角三角板如图所示,∠1=40°,则∠2=( )A.50° B.60° C.70° D.80°【答案】D【解析】【分析】如图:根据直角三角形的性质可得,然后再根据两直线平行,同旁内角互补解答即可.【详解】解:如图:∵含30°直角三角形∴∵直尺两边平行∴∠1+∠2+∠3=180°∴.故答案为D.【点睛】本题考查了直角三角形的性质和平行线的性质,其中灵活运用两直线平行、同旁内角互补的性质是解答本题的关键.【2021玉林第8题】点D,E分别是三角形ABC的边AB,AC的中点,如图,求证:且证明:延长DE到F, 使EF=DE,连接FC,DC,AF,又AE=EC,则四边形ADCF是平行四边形,接着以下是排序错误的证明过程;①;②;③四边形DBCF是平行四边形;④且则正确的证明排序应是:( )A.②③①④ B.②①③④ C.①③④② D.①③②④【答案】A【解析】【分析】根据已经证明出四边形ADCF是平行四边形,则利用平行四边形的性质可得,可得,证出四边形DBCF是平行四边形,得出,且,即可得出结论且,对照题中步骤,即可得出答案.【详解】解:四边形ADCF是平行四边形,,,四边形DBCF是平行四边形,,且;,;且;对照题中四个步骤,可得②③①④正确;故答案选:A.【点睛】本题考查平行四边形性质与判定综合应用;当题中出现中点的时候,可以利用中线倍长的辅助线做法,证明平行四边形后要记得用平行四边形的性质继续解题.【2021黔西南州第6题】如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1的度数为( )A.37° B.43° C.53° D.54°【答案】C【解析】【分析】先根据平行线的性质得出,再根据即可求解.【详解】∵AB∥CD,∴∠2=∠3=37°,∵∠FEG=90°,∴∴∠1=90°-∠3=90°-37°=53°故选:C.【点睛】本题主要考查平行线的性质和平角的定义,掌握平行线的性质是解题的关键.【2021潜东南州第5题】如图,将矩形ABCD沿AC折叠,使点B落在点B′处,B′C交AD于点E,若∠1=25°,则∠2等于( )A.25° B.30° C.50° D.60°【答案】C【解析】【分析】由折叠的性质可得出∠ACB′的度数,由矩形的性质可得出AD∥BC,再利用“两直线平行,内错角相等”可求出∠2的度数.【详解】解:由折叠的性质可知:∠ACB′=∠1=25°.∵四边形ABCD为矩形,∴AD∥BC,∴∠2=∠1+∠ACB′=25°+25°=50°.故选:C.【点睛】本题考查了矩形的折叠问题,解答关键是注意应用折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的性质.【2021铜仁第3题】如图,直线AB∥CD,∠3=70°,则∠1=( )A.70° B.100° C.110° D.120°【答案】C【解析】【分析】直接利用平行线的性质得出∠1=∠2,进而得出答案.【详解】∵直线AB∥CD,∴∠1=∠2,∵∠3=70°,∠2+∠3=180°,∴∠2=180°﹣∠3=180°﹣70°=110°,∴∠1=110°.故选:C.【点睛】此题主要考查了平行线的性质,求出∠2=110°是解答本题的关键.【2021遵义第3题】一副直角三角板如图放置,使两三角板的斜边互相平行,每块三角板的直角顶点都在另一三角板的斜边上,则∠1的度数为( )A.30° B.45° C.55° D.60°【答案】B【解析】【分析】根据平行线的性质即可得到结论.【详解】解:如图∵AB∥CD,∴∠1=∠D=45°,故选:B.【点睛】本题考查了平行线的性质以及直角三角板的各角度数,解答关键是根据利用平行线的性质找到相应角度之间的关系.【2021河南第4题】如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为( )A.100° B.110° C.120° D.130°【答案】B【分析】根据平行线的性质即可得到结论.【解答】解:∵l1∥l2,∠1=70°,∴∠3=∠1=70°,∵l3∥l4,∴∠2=180°﹣∠3=180°﹣70°=110°,故选:B.【点评】此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补.【2021哈尔宾第10题】如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )A.= B.= C.= D.=【答案】C【分析】根据平行线分线段成比例性质进行解答便可.【解答】解:∵EF∥BC,∴,∵EG∥AB,∴,∴,故选:C.【点评】本题主要考查了平行线分线段成比例性质,关键是熟记定理,找准对应线段. 解题的关键是:熟记两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补.灵活运用平行线的性质与判定。 要点一、两条直线的位置关系1.同一平面内两条直线的位置关系:相交与平行要点诠释:(1)只有一个公共点的两条直线叫做相交直线,这个公共点叫做交点.(2)在同一平面内不相交的两条直线叫做平行线.平行用符号“∥”表示.2.对顶角、补角、余角(1)定义:①由两条直线相交构成的四个角中,有公共顶点且两边互为反向延长线的两个角叫做对顶角.②如果两个角的和是180°,那么这两个角互为补角,简称互补,其中一个角叫做另一个角的补角.类似地,如果两个角的和是90°,那么这两个角互为余角.简称互余,其中一个角叫做另一个角的余角.(2)性质:同角或等角的余角相等.同角或等角的补角相等.对顶角相等.3.垂线 (1)垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足.垂直用符号“⊥”表示,如下图.(2)垂线的性质:①在同一平面内,过一点有且只有一条直线与已知直线垂直.②垂线段最短.(3)点到直线的距离:从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.要点二、平行线的判定与性质1.平行线的判定判定方法1:同位角相等,两直线平行.判定方法2:内错角相等,两直线平行.判定方法3:同旁内角互补,两直线平行.要点诠释:根据平行线的定义和平行公理的推论,平行线的判定方法还有:(1)平行线的定义:在同一平面内,如果两条直线没有交点(不相交),那么两直线平行.(2)如果两条直线都平行于第三条直线,那么这两条直线平行(平行线的传递性).(3)在同一平面内,垂直于同一直线的两条直线平行.(4)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.2.平行线的性质性质1:两直线平行,同位角相等;性质2:两直线平行,内错角相等;性质3:两直线平行,同旁内角互补.要点诠释:根据平行线的定义和平行公理的推论,平行线的性质还有:(1)若两条直线平行,则这两条直线在同一平面内,且没有公共点.(2)如果一条直线与两条平行线中的一条直线垂直,那么它必与另一条直线垂直.3.两条平行线间的距离如图,直线AB∥CD,EF⊥AB于E,EF⊥CD于F,则称线段EF的长度为两平行线AB与CD间的距离.要点诠释:(1)两条平行线之间的距离处处相等.(2)初中阶级学习了三种距离,分别是两点间的距离、点到直线距离、平行线间的距离.这三种距离的共同点在于都是线段的长度,它们的区别是两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是一条直线上的一点到与之平行的另一直线的距离.(3)如何理解 “垂线段”与 “距离”的关系:垂线段是一个图形,距离是线段的长度,是一个量,它们之间不能等同.1.如图,,一块含的直角三角板的一个顶点落在其中一条直线上,若,则的度数为( )A. B. C. D.【答案】A【解析】【分析】作平行a和b的平行线,再根据平行的性质可知,再算出即可得出.【详解】如图所示,过直角顶点作c∥a,∵,∴a∥b∥c,∴,∴,∴.故选A.【点睛】本题考查平行的性质,关键在于利用割补法将直角分成两个角度进行转换.2.如图,在中,,点H、E、F分别是边、、的中点,若,则的值为( )A.3 B.4 C.5 D.6【答案】B【解析】【分析】根据直角三角形的性质求出AB,根据三角形中位线定理计算即可.【详解】∵∠ACB=90°,点H是边AB的中点,∴AB=2CH,∵点E、F分别是边AC、BC的中点,∴AB=2EF∴CH=EF∵,∴=4故选:B.【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.3.如图,菱形中,E,F分别是,的中点,若,则菱形的周长为( )A.20 B.30 C.40 D.50【答案】C【解析】【分析】由题意可知EF为△ABD的中位线,可求出AB的长,由于菱形四条边相等即可得到周长.【详解】解:∵E,F分别是,的中点,∴EF为△ABD的中位线,∴,∵四边形是菱形,∴,∴菱形的周长为故选:C.【点睛】本题考查了三角形的中位线,菱形的性质,发现EF为△ABD的中位线是解题的关键.4.将一副三角尺如图摆放,点E在上,点D在的延长线上,,则的度数是( )A.15° B.20° C.25° D.30°【答案】A【解析】【分析】根据三角板的特点可知∠ACB=45°、∠DEF=30°,根据可知∠CEF=∠ACB=45°,最后运用角的和差即可解答.【详解】解:由三角板的特点可知∠ACB=45°、∠DEF=30°∵∴∠CEF=∠ACB=45°,∴∠CED=∠CEF-∠DEF=45°-30°=15°.故答案为A.【点睛】本题考查了三角板的特点、平行线的性质以及角的和差,其中掌握平行线的性质是解答本题的关键.5.如图,一块直角三角板的60度的顶点A与直角顶点C分别在平行线上,斜边AB平分,交直线GH于点E,则的大小为( )A. B. C. D.【答案】C【解析】【分析】利用角平分线的性质求得∠DAE的度数,利用平行线的性质求得∠ACE的度数,即可求解.【详解】∵AB平分,∠CAB=60,∴∠DAE=60,∵FD∥GH,∴∠ACE+∠CAD=180,∴∠ACE=180-∠CAB-∠DAE=60,∵∠ACB=90,∴∠ECB=90-∠ACE=30,故选:C.【点睛】本题考查了角平分线的定义,平行线的性质,用到的知识点为:两直线平行,同旁内角互补.1.如图,在菱形中,对角线相交于点为中点,.则线段的长为:( )A. B. C. D.【答案】B【解析】【分析】因为菱形的对角线互相垂直且平分,从而有,,,又因为H为BC中点,借助直角三角形斜边上的中线等于斜边的一半即可作答.【详解】解:∵四边形ABCD是菱形∴,,∴△BOC是直角三角形∴∴BC=5∵H为BC中点∴故最后答案为.【点睛】本题考查了菱形的性质、勾股定理、直角三角形斜边上的中线等于斜边的一半,其中知道菱形的性质,对角线互相垂直且平分是解题的关键.2.如图摆放的一副学生用直角三角板,,与相交于点G,当时,的度数是( )A.135° B.120° C.115° D.105°【答案】D【解析】【分析】过点G作,则有,,又因为和都是特殊直角三角形,,可以得到,有即可得出答案.【详解】解:过点G作,有,∵在和中,∴∴,∴故的度数是105°.【点睛】本题主要考查了平行线的性质和三角形内角和定理,其中平行线的性质为:两直线平行,内错角相等;三角形内角和定理为:三角形的内角和为180°;其中正确作出辅助线是解本题的关键.3.如图,AB∥CD,点P为CD上一点,PF是∠EPC的平分线,若∠1=55°,则∠EPD的大小为( )A.60° B.70° C.80° D.100°【答案】B【分析】根据平行线和角平分线的定义即可得到结论.【解答】解:∵AB∥CD,∴∠1=∠CPF=55°,∵PF是∠EPC的平分线,∴∠CPE=2∠CPF=110°,∴∠EPD=180°﹣110°=70°,故选:B.【点评】本题考查了平行线的性质以及角平分线的定义,熟练掌握平行线的性质是解题的关键. 4.如图,在ABC中,AB=AC,∠C=65°,点D是BC边上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )A.120° B.130° C.145° D.150°【答案】B【解析】【分析】根据等腰三角形的性质得到∠B=∠C,利用平行线的性质得到∠ EDC=∠B,利用三角形的外角性质即可求解.【详解】∵AB=AC,∴∠B=∠C=65°,∵DF∥AB,∴∠ EDC=∠B=65°,∴∠FEC=∠EDC+∠C=65°+65°=130°.故选:B.【点睛】本题考查了等腰三角形的性质,平行线的性质,三角形的外角性质,需熟练掌握.5.将含30°角的一个直角三角板和一把直尺如图放置,若,则等于()A.80° B.100° C.110° D.120°【答案】C【解析】【分析】如图,先根据平行线性质求出∠3,再求出∠4,根据四边形内角和为360°即可求解.【详解】解:如图,由题意得DE∥GF,∴∠1=∠3=50°,∴∠4=180°-∠3=130°,∴在四边形ACMN中,∠2=360°-∠A-∠C-∠4=110°.故选:C【点睛】本题考查了平行线的性质,四边形的内角和定理,熟知相关定理是解题关键.6.如图,在四边形ABCD中,CD∥AB,AC⊥BC,若∠B=50°,则∠DCA等于A.30°B.35°C.40°D.45°【答案】C【分析】由AC⊥BC可得∠ACB=90°,又∠B=50°,根据直角三角形两个锐角互余可得∠CAB=40°,再根据平行线的性质可得∠DCA=∠CAB=40°.【解答】解:∵AC⊥BC,∴∠ACB=90°,又∵∠B=50°,∴∠CAB=90°﹣∠B=40°,∵CD∥AB,∴∠DCA=∠CAB=40°.故选:C.【点评】本题主要考查了平行线的性质以及直角三角形的性质,根据题意得出∠CAB的度数是解答本题的关键.7.如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )A.2 B.2.5 C.3 D.4【答案】B【解析】【分析】利用勾股定理求得AB=10;然后由直角三角形斜边上的中线等于斜边的一半求得CD的长度;结合题意知线段BF是△CDE的中位线,则BF=CD.【详解】解:∵在Rt△ABC中,∠ACB=90°,AC=8,BC=6,∴AB===10.又∵CD为中线,∴CD=AB=5.∵F为DE中点,BE=BC,即点B是EC的中点,∴BF是△CDE的中位线,则BF=CD=2.5.故选:B.【点睛】本题主要考查了勾股定理,三角形中位线定理,直角三角形斜边上的中线,此题的突破口是推知线段CD的长度和线段BF是△CDE的中位线.
相关试卷
这是一份专题08 一次函数性质(选择题)-备战2021年中考数学临考题号押题(全国通用版)(28348090),文件包含专题08一次函数性质选择题解析版doc、专题08一次函数性质选择题原卷版doc等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
这是一份专题07 二次函数图象性质(选择题)-备战2021年中考数学临考题号押题(全国通用版),文件包含专题07二次函数图象性质选择题解析版doc、专题07二次函数图象性质选择题原卷版doc等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
这是一份专题06 圆的性质及计算(选择题)-备战2021年中考数学临考题号押题(全国通用版),文件包含专题06圆的性质及计算选择题解析版doc、专题06圆的性质及计算选择题原卷版doc等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。










