十二年高考真题分类汇编(2010-2021) 数学 专题05 三角函数Word版（含解析）

这是一份十二年高考真题分类汇编(2010-2021) 数学 专题05 三角函数Word版（含解析），共40页。试卷主要包含了函数的最小正周期和最大值分别是等内容，欢迎下载使用。
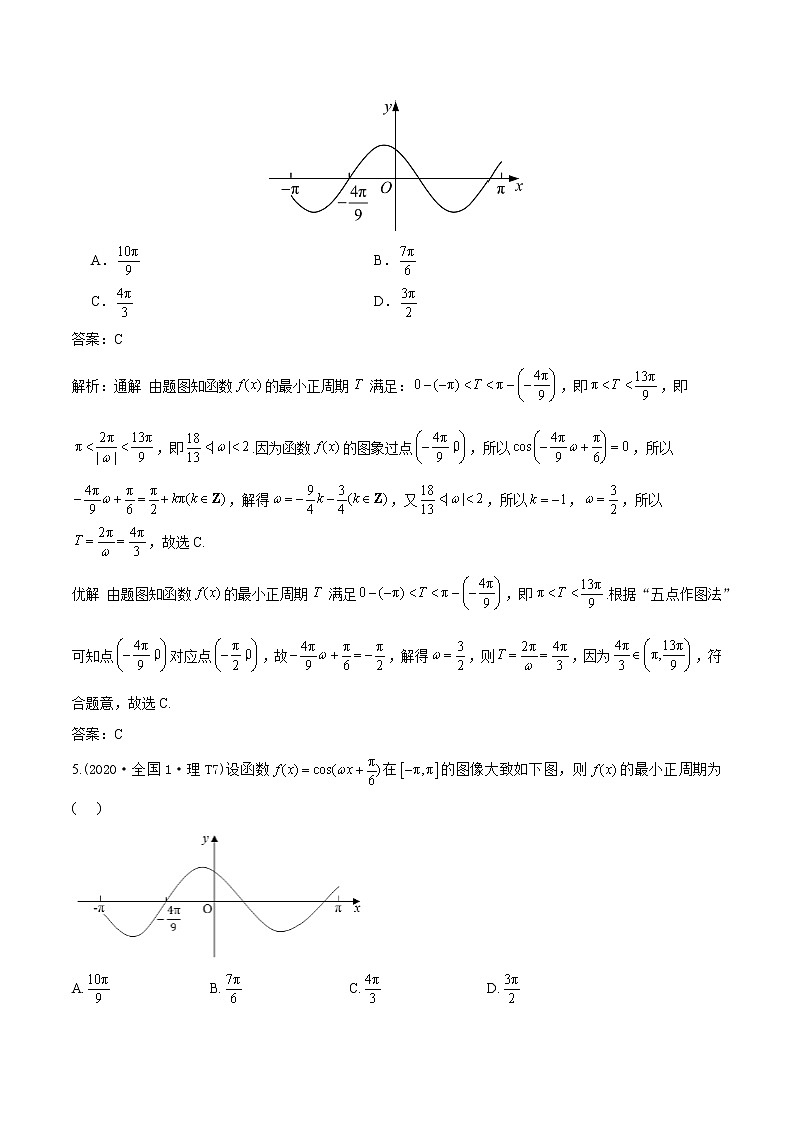
十二年高考真题分类汇编（2010—2021）数学专题05 三角函数一．选择题：1.(2021·全国1·文T4)函数的最小正周期和最大值分别是(   )A.3π和 B.3π和2 C.6π和 D.6π和2答案：C解析：本题考查三角函数的化简与性质.由三角函数，得其最小正周期为，最大值为.2.(2021·全国1·文T6)(   )A. B. C. D.答案：D解析：本题考查三角恒等变换的应用. .3.(2021·全国1·理T7)把函数图象上所有点的横坐标缩短到原来的倍，纵坐标不变，再把所得曲线向右平移个单位长度，得到函数的图象，则(   )A. B. C. D.答案：B解析：本题考查三角函数图象的伸缩变换和平移变换、三角函数的解析式.根据题目条件逆向思维，把函数的图象向左平移个单位长度，可得，再将图象上所有点的纵坐标不变，横坐标伸长为原来的2倍，可得，即.4．(2020·全国1·文T7)设函数在[−π，π]的图像大致如下图，则f（x）的最小正周期为A．   B．C．  D．答案：C解析：通解 由题图知函数的最小正周期满足：，即，即，即.因为函数的图象过点，所以，所以，解得，又，所以，，所以，故选C.优解 由题图知函数的最小正周期满足，即.根据“五点作图法”可知点对应点，故，解得，则，因为，符合题意，故选C.答案：C5.(2020·全国1·理T7)设函数在的图像大致如下图，则的最小正周期为(   )A. B. C. D. 解析：通解 由题图知，，，解得.设的最小正周期为，易知， ，，当且仅当时，符合题意，此时，.故选C.秒解 由题图知，且，，，解得，的最小正周期.故选C.6.(2019·全国2·理T10文T11)已知α∈0,,2sin 2α=cos 2α+1,则sin α=(　　)A. B. C. D.【答案】B【解析】∵2sin 2α=cos 2α+1,∴4sin αcos α=2cos2α.∵α∈（0,,∴cos α>0,sin α>0,∴2sin α=cos α.又sin2α+cos2α=1,∴5sin2α=1,即sin2α=.∵sin α>0,∴sin α=.故选B.7.(2019·全国2·文T8)若x1=,x2=是函数f(x)=sin ωx(ω>0)两个相邻的极值点,则ω=(　　)A.2 B. C.1 D.【答案】A【解析】由题意,得f(x)=sin ωx的周期T==2=π,解得ω=2,故选A.8.(2019·全国2·理T9)下列函数中,以为周期且在区间单调递增的是(　　)A.f(x)=|cos 2x| B.f(x)=|sin 2x|C.f(x)=cos|x| D.f(x)=sin|x|【答案】A【解析】y=|cos 2x|的图象为,由图知y=|cos 2x|的周期为,且在区间（）内单调递增,符合题意;y=|sin 2x|的图象为,由图知它的周期为,但在区间（）内单调递减,不符合题意;因为y=cos|x|=cos x,所以它的周期为2π,不符合题意;y=sin |x|的图象为,由图知其不是周期函数,不符合题意.故选A.9.(2019·天津·理T7)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是奇函数,将y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g(x).若g(x)的最小正周期为2π,且g（）=,则f（）=(　　)A.-2 B.- C. D.2【答案】C【解析】已知函数为奇函数,且|φ|<π,故φ=0.f(x)=Asin ωx.∴g(x)=Asin x.∵g(x)的最小正周期为2π,∴=2π,∴ω=1.∴g(x)=Asin x.由g（）=,得Asin ,∴A=2.∴f(x)=2sin 2x.∴f（）=2sin .故选C.10.(2019·北京·文T8)如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为(　　)A.4β+4cos β B.4β+4sin βC.2β+2cos β D.2β+2sin β【答案】B【解析】(方法一)如图,设圆心为O,连接OA,OB,半径r=2,∠AOB=2∠APB=2β,阴影部分Ⅰ(扇形)的面积S1=βr2=4β为定值,S△OAB=|OA||OB|sin 2β=2sin 2β为定值,全部阴影部分的面积S=S△PAB+S1-S△OAB.当P为弧AB的中点时S△PAB最大,最大值为(2|OA|sin β)(OP+|OA|cos β)=2sin β(2+2cos β)=4sin β+2sin 2β,所以全部阴影部分的面积S的最大值为4β+4sin β,故选B.(方法二)观察图象可知,当P为弧AB的中点时,阴影部分的面积S取最大值,此时∠BOP=∠AOP=π-β,面积S的最大值为βr2+S△POB+S△POA=4β+|OP||OB|sin(π-β)+|OP||OA|sin(π-β)=4β+2sin β+2sin β=4β+4sin β,故选B.11.(2019·全国3·理T12)设函数f(x)=sin(ω>0),已知f(x)在[0,2π]有且仅有5个零点,下述四个结论:①f(x)在(0,2π)有且仅有3个极大值点②f(x)在(0,2π)有且仅有2个极小值点③f(x)在单调递增④ω的取值范围是其中所有正确结论的编号是(　　)A.①④   B.②③ C.①②③           D.①③④【答案】D【解析】∵f(x)=sin(ω>0)在区间[0,2π]上有且仅有5个零点,∴5π≤2πω+<6π,解得≤ω<,故④正确.画出f(x)的图像(图略),由图易知①正确,②不正确.当0<x<时,<ωx+,又≤ω<,∴,∴③正确.综上可知①③④正确.故选D.12.(2018·北京·文T7)在平面直角坐标系中,是圆x2+y2=1上的四段弧(如图),点P在其中一段上,角α以Ox为始边,OP为终边.若tan α<cos α<sin α,则P所在的圆弧是(　　)A. B.C. D.【答案】C【解析】若P在上,则由角α的三角函数线知,cos α>sin α,排除A;若P在上,则tan α>sin α,排除B;若P在上,则tan α>0,cos α<0,sin α<0,排除D;故选C.13.(2018·全国1·文T11)已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos 2α=,则|a-b|=(　　)A. B. C. D.1【答案】B【解析】因为cos 2α=2cos2α-1=,所以cos2α=,sin2α=.所以tan2α=,tan α=±.由于a,b的正负性相同,不妨设tan α>0,即tan α=,由三角函数定义得a=,b=,故|a-b|=.14.(2018·全国3·T4)若sin α=,则cos 2α=(　　)A. B. C.- D.-【答案】B【解析】cos 2α=1-2sin2α=1-2×.15.(2018·全国3·文T6)函数f(x)=的最小正周期为(　　)A.      B.             C.π                D.2π【答案】C【解析】f(x)==sin 2x,∴f(x)的最小正周期是π.故选C.16.(2018·全国1·文T8)已知函数f(x)=2cos2x-sin2x+2,则(　　)A.f(x)的最小正周期为π,最大值为3B.f(x)的最小正周期为π,最大值为4C.f(x)的最小正周期为2π,最大值为3D.f(x)的最小正周期为2π,最大值为4【答案】B【解析】因为f(x)=2cos2x-(1-cos2x)+2=3cos2x+1=3×+1=cos 2x+,所以函数f(x)的最小正周期为=π,当cos 2x=1时,f(x)max=4.17.(2018·天津·理T6)将函数y=sin的图象向右平移个单位长度,所得图象对应的函数(　　)A.在区间上单调递增B.在区间上单调递减C.在区间上单调递增D.在区间上单调递减【答案】A【解析】函数y=siny=sin=sin 2x.当-+2kπ≤2x≤+2kπ,k∈Z,即-+kπ≤x≤+kπ,k∈Z时,y=sin 2x单调递增.当+2kπ≤2x≤+2kπ,k∈Z,即+kπ≤x≤+kπ,k∈Z时,y=sin 2x单调递减,结合选项,可知y=sin 2x在上单调递增.故选A.18.(2018·全国2·理T10)若f(x)=cos x-sin x在[-a,a]是减函数,则a的最大值是(　　)A. B. C. D.π【答案】A【解析】f(x)=cos x-sin x=-sin x·-cos x·=-sin x-,当x∈,即x-时,y=sin x-单调递增,y=-sin x-单调递减.∵函数f(x)在[-a,a]是减函数,∴[-a,a]⊆,∴0<a≤,∴a的最大值为.19.(2017·全国3·文T4)已知sin α-cos α=,则sin 2α=(　　)A.- B.- C. D.【答案】A【解析】∵(sin α-cos α)2=1-2sin αcos α=1-sin 2α=,∴sin 2α=-.20.(2017·山东·文T4)已知cos x=,则cos 2x=(　　)A.- B. C.- D.【答案】D【解析】cos 2x=2cos2x-1=2×-1=.21.(2017·全国3·理T6)设函数f(x)=cos,则下列结论错误的是(　　)A.f(x)的一个周期为-2π B.y=f(x)的图象关于直线x=对称C.f(x+π)的一个零点为x= D.f(x)在单调递减【答案】D【解析】由f(x)=cos的【解析】式知-2π是它的一个周期,故A中结论正确;将x=代入f(x)=cos,得f=-1,故y=f(x)的图象关于直线x=对称,故B中结论正确;f(x+π)=cos,当x=时,f(x+π)=cos=0,故C中结论正确;当x∈时,x+,显然f(x)先单调递减再单调递增,故D中结论错误.22.(2017·全国2·文T3)函数f(x)=sin的最小正周期为(　　)A.4π B.2π C.π D.【答案】C【解析】T==π,故选C.23.(2017·天津·T7)设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π,若f=2,f=0,且f(x)的最小正周期大于2π,则(　　)A.ω=,φ= B.ω=,φ=-C.ω=,φ=- D.ω=,φ=【答案】A【解析】∵f（=2,f（）=0,且f(x)的最小正周期大于2π,∴f(x)的最小正周期为4（=3π.∴ω=,∴f(x)=2sin （x+φ）.∴2sin （+φ）=2,∴φ=2kπ+,k∈Z.又|φ|<π,∴取k=0,得φ=.24.(2017·山东·文T7)函数y=sin 2x+cos 2x的最小正周期为(　　)A. B. C.π D.2π【答案】C【解析】因为y=sin 2x+cos 2x=2=2sin,所以其最小正周期T==π.25.(2017·全国1·理T9)已知曲线C1:y=cos x,C2:y=sin,则下面结论正确的是(　　)A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2【答案】D【解析】曲线C1的方程可化为y=cos x=sin,把曲线C1上各点的横坐标缩短到原来的,纵坐标不变,得曲线y=sin=sin 2,为得到曲线C2:y=sin 2,需再把得到的曲线向左平移个单位长度.26.(2017·全国3·文T6)函数f(x)=sin+cos的最大值为(　　)A. B.1 C. D.【答案】A【解析】因为cos=cos=sin,所以f(x)=sin+sinsin,故函数f(x)的最大值为.故选A.27.(2016·全国2·理T9)若cos,则sin 2α=(　　)A. B. C.- D.-【答案】D【解析】cos=2cos2-1=2×-1=-,且cos=cos=sin 2α,故选D.28.(2016·全国3·理T5)若tan α=,则cos2α+2sin 2α=(　　)A. B. C.1 D.【答案】A【解析】由tan α=,得cos2α+2sin 2α=.故选A.29.(2016·全国3·文T6)若tan θ=-,则cos 2θ=(　　)A.- B.- C. D.【答案】D【解析】cos 2θ=cos2θ-sin2θ=.故选D.30.(2016·全国1·理T12)已知函数f(x)=sin(ωx+φ),x=-为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在单调,则ω的最大值为(　　)A.11 B.9 C.7 D.5 【答案】B【解析】由题意知--=,k∈Z,即T=,k∈Z,又ω>0,所以ω=2k+1,k∈Z.又因为f(x)在单调,所以,T≥,即,ω≤12.因为ω>0,所以0<ω≤12.若ω=11,又|φ|≤,则φ=-,此时f(x)=sin 11x-,f(x)在单调递增,在单调递减,不满足条件;若ω=9,又|φ|≤,则φ=,此时f(x)=sin 9x+,满足f(x)在单调的条件,由此得ω的最大值为9.31.(2016·山东·理T7)函数f(x)=(sin x+cos x)(cos x-sin x)的最小正周期是(　　)A. B.π C. D.2π【答案】B【解析】f(x)=2sin×2cos=2sin,故最小正周期T==π,应选B.32.(2016·浙江·理T5)设函数f(x)=sin2x+bsin x+c,则f(x)的最小正周期(　　)A.与b有关,且与c有关 B.与b有关,但与c无关C.与b无关,且与c无关     D.与b无关,但与c有关【答案】B【解析】f(x)=sin2x+bsin x+c=+bsin x+c=-cos 2x+bsin x++c.当b=0时,f(x)=-cos 2x++c,周期T=π;当b≠0时,f(x)=-cos 2x+bsin x++c,∵y=-cos 2x的周期为π,y=bsin x的周期为2π,∴f(x)的周期T=2π.∴f(x)的最小正周期与b有关,但与c无关.故选B.33.(2016·全国2·文T3)函数y=Asin(ωx+φ)的部分图象如图所示,则(　　)A.y=2sin B.y=2sinC.y=2sin D.y=2sin【答案】A【解析】由题图知,A=2,周期T=2=π,所以ω==2,y=2sin(2x+φ).因为函数图象过点,所以2=2sin.所以+φ=2kπ+(k∈Z).令k=0,得φ=-,所以y=2sin,故选A.34.(2016·全国2·理T7)若将函数y=2sin 2x的图象向左平移个单位长度,则平移后图象的对称轴为(　　)A.x=(k∈Z)   B.x=(k∈Z)C.x=(k∈Z) D.x=(k∈Z)【答案】B【解析】由题意可知,将函数y=2sin 2x的图象向左平移个单位长度得函数y=2sin=2sin的图象,令2x++kπ(k∈Z),得x=(k∈Z).故选B.35.(2016·全国1·文T6)将函数y=2sin的图象向右平移个周期后,所得图象对应的函数为(　　)A.y=2sin B.y=2sinC.y=2sin D.y=2sin【答案】D【解析】由已知周期T=π,右移T=后得y=2sin=2sin的图象,故选D.36.(2016·四川·理T3)为了得到函数y=sin的图象,只需把函数y=sin 2x的图象上所有的点(　　)A.向左平行移动个单位长度B.向右平行移动个单位长度C.向左平行移动个单位长度D.向右平行移动个单位长度【答案】D【解析】y=sin=sin.37.(2016·北京·理T7)将函数y=sin图象上的点P向左平移s(s>0)个单位长度得到点P'.若P'位于函数y=sin 2x的图象上,则(　　)A.t=,s的最小值为 B.t=,s的最小值为C.t=,s的最小值为 D.t=,s的最小值为【答案】A【解析】设P'(x,y).由题意得t=sin,且P'的纵坐标与P的纵坐标相同,即y=.又P'在函数y=sin 2x的图象上,则sin 2x=,故点P'的横坐标x=+kπ(k∈Z)或+kπ(k∈Z),结合题意可得s的最小值为.38.(2016·全国2·文T11)函数f(x)=cos 2x+6cos 的最大值为(　　)A.4 B.5 C.6 D.7【答案】B【解析】因为f(x)=1-2sin2x+6sin x=-2sin x-2+,而sin x∈[-1,1],所以当sin x=1时,f(x)取最大值5,故选B.39.(2015·福建·文T6)若sin α=-,且α为第四象限角,则tan α的值等于(　　)A. B.- C. D.-【答案】D【解析】∵sin α=-,且α为第四象限角,∴cos α=.∴tan α==-.40.(2015·全国1·理T2,)sin 20°cos 10°-cos 160°sin 10°=(　　)A.- B. C.- D.【答案】D【解析】sin 20°cos 10°-cos 160°sin 10°=sin 20°cos 10°+cos 20°sin 10°=sin(10°+20°)=sin 30°=.41.(2015·重庆·理T9)若tan α=2tan,则=(　　)A.1 B.2 C.3 D.4 【答案】C【解析】因为tan α=2tan,所以==3.42.(2015·重庆·文T6)若tan α=,tan(α+β)=,则tan β=(　　)A. B. C. D.【答案】A【解析】tan β=tan[(α+β)-α]==.43.(2015·安徽·理T10)已知函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x=时,函数f(x)取得最小值,则下列结论正确的是(　　)A.f(2)<f(-2)<f(0) B.f(0)<f(2)<f(-2)C.f(-2)<f(0)<f(2) D.f(2)<f(0)<f(-2)【答案】A【解析】将要比较的函数值化归到函数的同一单调区间内.∵f(x)的最小正周期为π,∴f(-2)=f(π-2).又当x=时,f(x)取得最小值,故当x=时,f(x)取得最大值,是函数f(x)的一个递减区间.又∵<π-2<2<,∴f(π-2)>f(2),即f(-2)>f(2).再比较0,π-2与对称轴x=距离的大小.∵π-2--0-=-2--2>0,∴f(0)>f(π-2),即f(0)>f(-2),综上,f(0)>f(-2)>f(2).故选A.44.(2015·全国1·T8)函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为(　　) A.,k∈ZB.,k∈ZC.,k∈ZD.,k∈Z【答案】D【解析】不妨设ω>0,由函数图象可知,其周期为T=2×=2,所以=2,解得ω=π.所以f(x)=cos(πx+φ).由图象可知,当x=时,f(x)取得最小值,即f=cos=-1,解得+φ=2kπ+π(k∈Z),解得φ=2kπ+(k∈Z).令k=0,得φ=,所以f(x)=cos.令2kπ≤πx+≤2kπ+π(k∈Z),解得2k-≤x≤2k+(k∈Z).所以函数f(x)=cos的单调递减区间为(k∈Z).结合选项知选D.45.(2015·陕西·理T3文T14)如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin +k.据此函数可知,这段时间水深(单位:m)的最大值为(　　)A.5 B.6 C.8 D.10【答案】C【解析】因为sin∈[-1,1],所以函数y=3sin+k的最小值为k-3,最大值为k+3.由题图可知k-3=2,解得k=5.所以y的最大值为k+3=5+3=8.故选C.46.(2015·山东·理T3文T4)要得到函数y=sin的图象,只需将函数y=sin 4x的图象(　　)A.向左平移个单位 B.向右平移个单位C.向左平移个单位 D.向右平移个单位【答案】B【解析】∵y=sin=sin,∴只需将函数y=sin 4x的图象向右平移个单位即可.47.(2014·全国1·T文2)若tan α>0,则(　　)A.sin α>0   B.cos α>0C.sin 2α>0 D.cos 2α>0【答案】C【解析】由tan α>0知角α是第一或第三象限角,当α是第一象限角时,sin 2α=2sin αcos α>0;当α是第三象限角时,sin α<0,cos α<0,仍有sin 2α=2sin αcos α>0,故选C.48.(2014·大纲全国·文T2)已知角α的终边经过点(-4,3),则cos α=(　　)A. B. C.- D.-【答案】D【解析】设角α的终边上点(-4,3)到原点O的距离为r,r==5,∴由余弦函数的定义,得cos α==-,故选D.49.(2014·全国1·理T8)设α∈,β∈,且tan α=,则(　　)A.3α-β= B.3α+β=C.2α-β= D.2α+β=【答案】C【解析】由已知,得,∴sin αcos β=cos α+cos αsin β.∴sin αcos β-cos αsin β=cos α.∴sin(α-β)=cos α,∴sin(α-β)=sin.∵α∈,β∈,∴-<α-β<,0<-α<,∴α-β=-α,∴2α-β=.故选C.50.(2014·大纲全国·理T3)设a=sin 33°,b=cos 55°,c=tan 35°,则(　　)A.a>b>c B.b>c>aC.c>b>a D.c>a>b【答案】C【解析】∵a=sin 33°,b=cos 55°=sin 35°,c=tan 35°=,∴>sin 35°>sin 33°.∴c>b>a.故选C.51.(2014·全国1·文T7)在函数①y=cos|2x|,②y=|cos x|,③y=cos,④y=tan中,最小正周期为π的所有函数为(　　)A.①②③ B.①③④ C.②④ D.①③【答案】A【解析】由于y=cos|2x|=cos 2x,所以该函数的周期为=π;由函数y=|cos x|的图象易知其周期为π;函数y=cos的周期为=π;函数y=tan（2x-）的周期为,故最小正周期为π的函数是①②③,故选A.52.(2014·全国1·理T6)如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示成x的函数f(x),则y=f(x)在[0,π]的图象大致为(　　)【答案】C【解析】由题意知|OM|=|cos x|,f(x)=|OM||sin x|=|sin xcos x|=|sin 2x|,由此可知C项中图符合.故选C.53.(2014·浙江·理T4)为了得到函数y=sin 3x+cos 3x的图象,可以将函数y=cos 3x的图象 (　　)A.向右平移个单位 B.向左平移个单位C.向右平移个单位 D.向左平移个单位【答案】C【解析】y=sin 3x+cos 3x=coscos,因此需将函数y=cos 3x的图象向右平移个单位.故选C.54.(2013·浙江·理T6)已知α∈R,sin α+2cos α=,则tan 2α=(　　)A. B. C.- D.-【答案】C【解析】由sin α+2cos α=,得sin α=-2cos α.       ①把①式代入sin2α+cos2α=1中可解出cos α=或cos α=,当cos α=时,sin α=;当cos α=时,sin α=-.∴tan α=3或tan α=-,∴tan 2α=-.55.(2013·大纲全国·文T2)已知α是第二象限角,sin α=,则cos α=(　　)A.- B.- C. D.【答案】A【解析】∵α是第二象限角,∴cos α=-=-=-.故选A.56.(2013·广东·文T4)已知sin,那么cos α=(　　)A.- B.- C. D.【答案】C【解析】∵sin=sin=cos α=,∴cos α=.57.(2013·全国2·文T6)已知sin 2α=,则cos2=(　　)A. B. C. D.【答案】A【解析】由降幂公式变形,可得cos2.58.(2012·全国·理T9)已知ω>0,函数f(x)=sin单调递减,则ω的取值范围是 (　　)A. B. C. D.(0,2]【答案】A【解析】结合y=si n ωx的图象可知y=sin ωx在单调递减,而y=sin（ωx+）=sin[ω（x+）],可知y=sin ωx的图象向左平移个单位之后可得y=sin的图象,故y=sin单调递减,故应有,解得≤ω≤.59.(2012·全国·文T9)已知ω>0,0<φ<π,直线x=和x=是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则φ=(　　)A. B. C. D.【答案】A【解析】由题意可知函数f(x)的周期T=2×=2π,故ω=1,∴f(x)=sin(x+φ).令x+φ=kπ+,将x=代入可得φ=kπ+,∵0<φ<π,∴φ=.60.(2011·全国·理T5文T7)已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos 2θ=(　　)A.- B.- C. D.【答案】B【解析】由三角函数的定义知tan θ=2,且θ为第一或第三象限角,故由“1”的代换得cos 2θ=cos2θ-sin2θ==-.61.(2011·全国·理T11)设函数f(x)=sin(ωx+φ)+cos(ωx+φ)的最小正周期为π,且f(-x)=f(x),则(　　)A.f(x)在单调递减B.f(x)在单调递减C.f(x)在单调递增D.f(x)在单调递增【答案】A【解析】∵f(x)=sin(ωx+φ)+cos(ωx+φ)=sinωx+φ+,又∵f(x)的最小正周期为π,∴=π,即ω=2.又f(-x)=f(x),故f(x)是偶函数,即φ++kπ(k∈Z),φ=kπ+(k∈Z).因|φ|<,取k=0,则φ=,从而f(x)=cos 2x,且在上单调递减,故选A.62.(2011·全国·文T11)设函数f(x)=sin+cos,则(　　)A.y=f(x)在单调递增,其图象关于直线x=对称B.y=f(x)在单调递增,其图象关于直线x=对称C.y=f(x)在单调递减,其图象关于直线x=对称D.y=f(x)在单调递减,其图象关于直线x=对称【答案】D【解析】∵f(x)=sin+cossincos 2x,∴f(x)在内单调递减,且图象关于直线x=对称.故选D.63.(2010·全国·理T9)若cosα=-,α是第三象限的角,则=(　　)A.- B. C.2 D.-2【答案】A【解析】∵cosα=-,α为第三象限角,∴sin α=-.=-.64.(2010·全国·文T10)若cos α=-,α是第三象限的角,则sin等于(　　)A.- B.C.- D.【答案】A【解析】因为α是第三象限的角,所以sin α<0.sinα=-=-=-.故sin=sin αcos+cos αsin=(sin α+cos α)==-.65.(2010·全国·文T6)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0( ,-),角速度为1,那么点P到x轴的距离d关于时间t的函数大致图象为(　　)【答案】C【解析】因为d是圆周上的点P到x轴的距离,所以每转半周,即π弧度,d的值就会周期性出现,又质点P的角速度为1,可知,该函数的周期为T==π.起始点为P0(,-)在第四象限,对应的d=,逆时针旋转到x轴时,d的值逐渐减小到0且此时t=.综上,只有C项满足,故选C. 二．填空题：1.(2019·江苏·T13)已知=-,则sin2α+的值是 　. 【答案】【解析】由=-,得3tan2α-5tan α-2=0,解得tan α=2或tan α=-.又sin=sin 2αcos+cos 2αsin=(sin 2α+cos 2α)==.     (*)①当tan α=2时,(*)式=;②当tan α=-时,(*)式=.综上,sin.2.(2019·全国1·文T15)函数f(x)=sin-3cos x的最小值为. 【答案】-4【解析】f(x)=sin-3cos x=-cos 2x-3cos x=-2cos2x-3cos x+1=-2.∵-1≤cos x≤1,∴当cos x=1时,f(x)min=-4.故函数f(x)的最小值是-4.3.(2018·全国2·理T15)已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)=　. 【答案】—【解析】∵(sin α+cos β)2+(cos α+sin β)2=1,∴sin2α+cos2β+cos2α+sin2β+2sin αcos β+2sin βcos α=1+1+2sin(α+β)=1.∴sin(α+β)= .4.(2018·全国2·文T15)已知tanα-=,则tan α=_________. 【答案】【解析】∵tan,∴5tan α-5=1+tan α.∴tan α=.5.(2018·北京·理T11)设函数f(x)=cos(ω>0).若f(x)≤f对任意的实数x都成立,则ω的最小值为____________. 【答案】【解析】∵f(x)≤f对任意的实数x都成立,∴当x=时,f(x)取得最大值,即f=cos=1,∴ω-=2kπ,k∈Z,∴ω=8k+,k∈Z.∵ω>0,∴当k=0时,ω取得最小值.6.(2018·全国3·理T15)函数f(x)=cos 在[0,π]的零点个数为　　. 【答案】3【解析】令f(x)=cos=0,得3x++kπ,k∈Z,∴x=,k∈Z.则在[0,π]的零点有.故有3个.7.(2018·全国1·理T16)已知函数f(x)=2sin x+sin 2x,则f(x)的最小值是　　. 【答案】【解析】由题意可得T=2π是f(x)=2sin x+sin 2x的一个周期,所以求f(x)的最小值可考虑求f(x)在[0,2π)上的值域.由f(x)=2sin x+sin 2x,得f'(x)=2cos x+2cos 2x=4cos2x+2cos x-2.令f'(x)=0,可得cos x=或cos x=-1,x∈[0,2π)时,解得x=或x=或x=π.因为f(x)=2sin x+sin 2x的最值只能在x=,x=,x=π或x=0时取到,且f,f=-,f(π)=0,f(0)=0,所以函数f(x)的最小值为-.8.(2018·江苏·T7)已知函数y=sin(2x+φ)-<φ<的图象关于直线x=对称,则φ的值为_______. 【答案】【解析】由题意可得sin=±1,解得+φ=+kπ(k∈Z),即φ=-+kπ(k∈Z).因为-<φ<,所以k=0,φ=-.9.(2017·北京·文T9)在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sin α=,则sin β=【答案】【解析】由角α与角β的终边关于y轴对称,得α+β=2kπ+π,k∈Z,即β=2kπ+π-α,k∈Z,故sin β=sin(2kπ+π-α)=sin α=.10.(2017·全国1·文T15)已知α∈,tan α=2,则cos=__________.【答案】【解析】由tan α=2,得sin α=2cos α.又sin2α+cos2α=1,所以cos2α=.因为α∈,所以cos α=,sin α=.因为cos=cos αcos+sin αsin,所以cos.11.(2017·北京·理T12)在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称.若sin α=,则cos(α-β)=________________. 【答案】-【解析】由角α与角β的终边关于y轴对称可得β=(2k+1)π-α,k∈Z,则cos(α-β)=cos[2α-(2k+1)π]=-cos 2α=2sin2α-1=2×-1=-.12.(2017·江苏·T5)若tan,则tan α=________. 【答案】【解析】因为tan,所以tan α=.13.(2017·全国2·理T14)函数f(x)=sin2x+cos x-的最大值是________.【答案】1【解析】由题意可知f(x)=1-cos2x+cos x-=-cos2x+cos x+=-+1.因为x∈,所以cos x∈[0,1].所以当cos x=时,函数f(x)取得最大值1.14.(2017·全国2·文T13)函数f(x)=2cos x+sin x的最大值为     　. 【答案】【解析】因为f(x)=2cos x+sin x=sin(x+φ)(其中tan φ=2),所以f(x)的最大值为.15.(2016·全国1·文T14)已知θ是第四象限角,且sin,则tan=　　.【答案】-【解析】∵sin,∴cos=cos.又θ是第四象限角,∴θ-是第三或第四象限角.∴sin=-.∴tan=-.16.(2016·四川·文T11)sin 750°= 　. 【答案】【解析】sin 750°=sin(720°+30°)=sin 30°=.17.(2016·四川·理T11)cos2-sin2=_________. 【答案】【解析】cos2-sin2=cos.18.(2016·浙江·T10)已知2cos2x+sin 2x=Asin(ωx+φ)+b(A>0),则A=,b=　　. 【答案】1【解析】因为2cos2x+sin 2x=1+cos 2x+sin 2x=sin+1,所以A=,b=1.19.(2016·全国3·理T14)函数y=sin x-cos x的图象可由函数y=sin x+cos x的图象至少向右平移_______个单位长度得到. 【答案】【解析】因为y=sin x+cos x=2sin,y=sin x-cos x=2sin（x-）=2sin[（x-）+],所以函数y=sin x-cos x的图象可由函数y=sin x+cos x的图象至少向右平移个单位长度得到.20.(2015·江苏·理T8)已知tan α=-2,tan(α+β)=,则tan β的值为　　. 【答案】3【解析】tan β=tan[(α+β)-α]===3.21.(2015·四川·理T12)sin 15°+sin 75°的值是_____________. 【答案】【解析】sin 15°+sin 75°=sin(45°-30°)+sin(45°+30°)=sin 45°cos 30°-cos 45°sin 30°+sin 45°cos 30°+cos 45°sin 30°=2sin 45°cos 30°=2×.22.(2015·四川·文T13)已知sin α+2cos α=0,则2sin αcos α-cos2α的值是　　. 【答案】-1【解析】由sin α+2cos α=0,得tan α=-2.所以原式===-1.23.(2015·天津·文T14)已知函数f(x)=sin ωx+cos ωx(ω>0),x∈R.若函数f(x)在区间(-ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为　. 【答案】【解析】f(x)=sin ωx+cos ωx=sin ωx+,因为f(x)在区间(-ω,ω)内单调递增,且函数图象关于直线x=ω对称,所以f(ω)必为一个周期上的最大值,所以有ω·ω+=2kπ+,k∈Z,所以ω2=+2kπ,k∈Z.又ω-(-ω)≤,即ω2≤,所以ω=.24.(2015·湖南·文T15)已知ω>0,在函数y=2sin ωx与y=2cos ωx的图象的交点中,距离最短的两个交点的距离为2,则ω=____________.【答案】【解析】如图所示,在同一直角坐标系中,作出函数y=2sin ωx与y=2cos ωx的图象,A,B为符合条件的两交点.则A,B,由|AB|=2,得=2,解得=2,即ω=.25.(2014·全国2·理T14)函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为　　. 【答案】1【解析】∵f(x)=sin(x+2φ)-2sin φcos(x+φ)=sin[(x+φ)+φ]-2sin φcos(x+φ)=sin(x+φ)cosφ+cos(x+φ)sin φ-2sin φcos(x+φ)=sin(x+φ)cosφ-cos(x+φ)sin φ=sin[(x+φ)-φ]=sin x.∴f(x)max=1.26.(2014·全国2·文T14)函数f(x)=sin(x+φ)-2sin φcos x的最大值为　　. 【答案】1【解析】∵f(x)=sin(x+φ)-2sin φcos x=sin xcos φ+cos xsin φ-2sin φcos x=sin xcos φ-cos xsin φ=sin(x-φ),∴f(x)max=1.27.(2014·重庆·文T13)将函数f(x)=sin(ωx+φ)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移个单位长度得到y=sin x的图象,则f=______. 【答案】【解析】本题可逆推,将y=sin x的图象向左平移个单位长度得到y=sin的图象,再保持纵坐标不变,横坐标伸长为原来的两倍,得到f(x)=sin的图象.所以f=sin=sin.28.(2014·全国2·理T14)函数f(x)=sin(x+2φ)-2sin φcos(x+φ)的最大值为　　.【答案】1【解析】∵f(x)=sin(x+2φ)-2sin φcos(x+φ)=sin[(x+φ)+φ]-2sin φcos(x+φ)=sin(x+φ)cosφ+cos(x+φ)sin φ-2sin φcos(x+φ)=sin(x+φ)cosφ-cos(x+φ)sin φ=sin[(x+φ)-φ]=sin x.∴f(x)max=1.29.(2014·全国2·文T14)函数f(x)=sin(x+φ)-2sin φcos x的最大值为　　. 【答案】1【解析】∵f(x)=sin(x+φ)-2sin φcos x=sin xcos φ+cos xsin φ-2sin φcos x=sin xcos φ-cos xsin φ=sin(x-φ),∴f(x)max=1.30.(2013·全国2·理T15)设θ为第二象限角,若tan,则sin θ+cos θ=　　.【答案】-【解析】由tan,得tan θ=-,即sin θ=-cos θ.将其代入sin2θ+cos2θ=1,得cos2θ=1.因为θ为第二象限角,所以cos θ=-,sin θ=,sin θ+cos θ=-.31.(2013·全国2·文T16)函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移个单位后,与函数y=sin的图象重合,则φ=_________. 【答案】A【解析】由降幂公式变形,可得cos2.32.(2013·全国1·理T15文T16)设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=　　. 【答案】【解析】∵f(x)=sin x-2cos x=sin(x-φ),其中sin φ=,cos φ=.当x-φ=2kπ+(k∈Z)时,f(x)取最大值.即θ-φ=2kπ+(k∈Z),θ=2kπ++φ(k∈Z).∴cos θ=cos=-sin φ=-.33.(2011·江西·理T14)已知角θ的顶点为坐标原点,始边为x轴的正半轴.若P(4,y)是角θ终边上一点,且sin θ=-,则y=　　. 【答案】-8【解析】∵sin θ=-<0及P(4,y)是角θ终边上一点,∴θ为第四象限角.又由三角函数的定义得=-,且y<0,∴y=-8(合题意),y=8(舍去).故y=-8.三．大题：1.(2019·浙江·T18)设函数f(x)=sin x,x∈R.(1)已知θ∈[0,2π),函数f(x+θ)是偶函数,求θ的值;(2)求函数y=fx+2+fx+2的值域.【解析】(1)因为f(x+θ)=sin(x+θ)是偶函数,所以,对任意实数x都有sin(x+θ)=sin(-x+θ),即sin xcos θ+cos xsin θ=-sin xcos θ+cos xsin θ,故2sin xcos θ=0,所以cos θ=0.又θ∈[0,2π),因此θ=.(2)y=fx+2+fx+2=sin2x++sin2x+==1-cos 2x-sin 2x=1-cos2x+.因此,函数的值域是1-,1+.2.(2018·浙江·T18)已知角α的顶点与原点O重复,始边与x轴的非负半轴重合,它的终边过点P.(1)求sin(α+π)的值;(2)若角β满足sin(α+β)=,求cos β的值.【解析】(1)由角α的终边过点P,得sin α=-,所以sin(α+π)=-sin α=.(2)由角α的终边过点P,得cos α=-,由sin(α+β)=,得cos(α+β)=±.由β=(α+β)-α,得cos β=cos(α+β)cos α+sin(α+β)sin α,所以cos β=-或cos β=.3.(2018·江苏·T16)已知α,β为锐角,tanα=,cos(α+β)=-.(1)求cos 2α的值;(2)求tan(α-β)的值.【解析】(1)因为tan α=,tan α=,所以sin α=cos α.因为sin2α+cos2α=1,所以cos2α=,因此,cos 2α=2cos2α-1=-.(2)因为α,β为锐角,所以α+β∈(0,π).又因为cos(α+β)=-,所以sin(α+β)=,因此tan(α+β)=-2.因为tan α=,所以tan 2α==-,因此,tan(α-β)=tan[2α-(α+β)]==-.4.(2018·北京·文T16)已知函数f(x)=sin2x+sin xcos x.(1)求f(x)的最小正周期;(2)若f(x)在区间上的最大值为,求m的最小值.【解析】(1)因为f(x)=sin 2x=sin 2x-cos 2x+=sin,所以f(x)的最小正周期为T==π.(2)由(1)知f(x)=sin.因为x∈,所以2x-.要使f(x)在上的最大值为,即y=sin上的最大值为1.所以2m-,即m≥.所以m的最小值为.5.(2018·上海·T18)设常数a∈R,函数f(x)=asin 2x+2cos2x.(1)若f(x)为偶函数,求a的值;(2)若f+1,求方程f(x)=1-在区间[-π,π]上的解.【解析】(1)∵f(x)=asin 2x+2cos2x,∴f(-x)=-asin 2x+2cos2x.∵f(x)为偶函数,∴f(-x)=f(x),∴-asin 2x+2cos2x=asin 2x+2cos2x,∴2asin 2x=0,∴a=0.(2)∵f+1,∴asin+2cos2=a+1=+1,∴a=,∴f(x)=sin 2x+2cos2x=sin 2x+cos 2x+1=2sin+1.∵f(x)=1-,∴2sin+1=1-,∴sin=-,∴2x+=-+2kπ或2x+π+2kπ,k∈Z,∴x=kπ-或x=kπ+,k∈Z.∵x∈[-π,π],∴x=-或-.∴所求方程的解为x=-或-.6.(2016·天津·理T15)已知函数f(x)=4tan xsincos.(1)求f(x)的定义域与最小正周期;(2)讨论f(x)在区间上的单调性.【解析】(1)f(x)的定义域为.f(x)=4tan xcos xcos=4sin xcos=4sin x=2sin xcos x+2sin2x-=sin 2x+(1-cos 2x)-=sin 2x-cos 2x=2sin,所以,f(x)的最小正周期T==π.(2)令z=2x-,函数y=2sin z的单调递增区间是,k∈Z.由-+2kπ≤2x-+2kπ,得-+kπ≤x≤+kπ,k∈Z.设A=,B=,易知A∩B=.所以,当x∈时,f(x)在区间上单调递增,在区间上单调递减.7.(2016·北京·文T16)已知函数f(x)=2sin ωxcos ωx+cos 2ωx(ω>0)的最小正周期为π.(1)求ω的值;(2)求f(x)的单调递增区间.【解析】(1)因为f(x)=2sin ωxcos ωx+cos 2ωx=sin 2ωx+cos 2ωx=sin,所以f(x)的最小正周期T=.依题意,=π,解得ω=1.(2)由(1)知f(x)=sin.函数y=sin x的单调递增区间为(k∈Z).由2kπ-≤2x+≤2kπ+,得kπ-≤x≤kπ+.所以f(x)的单调递增区间为(k∈Z).8.(2016·山东·文T17)设f(x)=2sin(π-x)sin x-(sin x-cos x)2(1)求f(x)的单调递增区间;(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g的值.【解析】(1)由f(x)=2sin(π-x)sin x-(sin x-cos x)2=2sin2x-(1-2sin xcos x)=(1-cos 2x)+sin 2x-1=sin 2x-cos 2x+-1=2sin-1,由2kπ-≤2x-≤2kπ+(k∈Z),得kπ-≤x≤kπ+(k∈Z),所以f(x)的单调递增区间是(k∈Z).(2)由(1)知f(x)=2sin-1,把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=2sin-1的图象,再把得到的图象向左平移个单位,得到y=2sin x+-1的图象,即g(x)=2sin x+-1.所以g=2sin-1=.9.(2015·广东·文T16)已知tan α=2. (1)求tan的值;(2)求的值.【解析】(1)tan==-3.(2)=====1.10.(2015·天津·理T15)已知函数f(x)=sin2x-sin2,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.【解析】(1)由已知,有f(x)==cos 2x=sin 2x-cos 2x=sin.所以,f(x)的最小正周期T==π.(2)因为f(x)在区间上是减函数,在区间上是增函数,f=-,f=-,f.所以,f(x)在区间上的最大值为,最小值为-.11.(2015·北京·理T15)已知函数f(x)=sin cos sin2.(1)求f(x)的最小正周期;(2)求f(x)在区间[-π,0]上的最小值.【解析】(1)因为f(x)=sin x-(1-cos x)=sin,所以f(x)的最小正周期为2π.(2)因为-π≤x≤0,所以-≤x+.当x+=-,即x=-时,f(x)取得最小值.所以f(x)在区间[-π,0]上的最小值为f=-1-.12.(2015·安徽·文T16)已知函数f(x)=(sin x+cos x)2+cos 2x.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.【解析】(1)因为f(x)=sin2x+cos2x+2sin xcos x+cos 2x=1+sin 2x+cos 2x=sin+1,所以函数f(x)的最小正周期为T==π.(2)由(1)的计算结果知,f(x)=sin+1.当x∈时,2x+,由正弦函数y=sin x在上的图象知,当2x+,即x=时,f(x)取最大值+1;当2x+,即x=时,f(x)取最小值0.综上,f(x)在上的最大值为+1,最小值为0.13.(2015·湖北·理T17)某同学用“五点法”画函数f(x)=Asin(ωx+φ) 在某一个周期内的图象时,列表并填入了部分数据,如下表:ωx+φ0π2πx   Asin(ωx+φ)05 -50(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象,若y=g(x)图象的一个对称中心为,求θ的最小值.【解析】(1)根据表中已知数据,解得A=5,ω=2,φ=-    .数据补全如下表:ωx+φ0π2πxAsin(ωx+φ)050-50且函数表达式为f(x)=5sin.(2)由(1)知f(x)=5sin,得g(x)=5sin.因为y=sin x的对称中心为(kπ,0),k∈Z.令2x+2θ-=kπ,k∈Z,解得x=-θ,k∈Z.由于函数y=g(x)的图象关于点成中心对称,令-θ=,k∈Z,解得θ=,k∈Z.由θ>0可知,当k=1时,θ取得最小值.14.(2014·天津·理T15)已知函数f(x)=cos xsincos2x+,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在闭区间上的最大值和最小值.【解析】(1)因为α∈,sin α=,所以cos α=-=-.故sin=sincos α+cossin α==-.(2)由(1)知sin 2α=2sin αcos α=2×=-,cos 2α=1-2sin2α=1-2×,所以cos=coscos 2α+sinsin 2α==-.15.(2014·江西·理T16)已知函数f(x)=sin(x+θ)+acos(x+2θ),其中a∈R,θ∈.(1)当a=,θ=时,求f(x)在区间[0,π]上的最大值与最小值;(2)若f=0,f(π)=1,求a,θ的值.【解析】(1)f(x)=sincos=(sin x+cos x)-sin x=cos x-sin x=sin,因为x∈[0,π],从而-x∈.故f(x)在[0,π]上的最大值为,最小值为-1.(2)由又θ∈,知cos θ≠0,解得16.(2014·山东·理T16)已知向量a=(m,cos 2x),b=(sin 2x,n),函数f(x)=a·b,且y=f(x)的图象过点和点.(1)求m,n的值;(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象,若y=g(x)图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.【解析】(1)由题意知f(x)=a·b=msin 2x+ncos 2x.因为y=f(x)的图象过点,所以即解得m=,n=1.(2)由(1)知f(x)=sin 2x+cos 2x=2sin.由题意知g(x)=f(x+φ)=2sin.设y=g(x)的图象上符合题意的最高点为(x0,2),由题意知+1=1,所以x0=0,即到点(0,3)的距离为1的最高点为(0,2).将其代入y=g(x)得sin=1,因为0<φ<π,所以φ=.因此g(x)=2sin=2cos 2x,由2kπ-π≤2x≤2kπ,k∈Z,得kπ-≤x≤kπ,k∈Z,所以函数y=g(x)的单调递增区间为,k∈Z.17.(2014·重庆·理T17)已知函数f(x)=sin(ωx+φ)≤φ<的图象关于直线x=对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)若f,求cos的值.【解析】(1)因f(x)的图象上相邻两个最高点的距离为π,所以f(x)的最小正周期T=π,从而ω==2.又因f(x)的图象关于直线x=对称,所以2·+φ=kπ+,k=0,±1,±2,….由-≤φ<得k=0,所以φ==-.(2)由(1)得fsin,所以sin.由<α<得0<α-,所以cos=.因此cos=sin α=sin=sincos+cossin=.18.(2014·四川·理T16文T17)已知函数f(x)=sin.(1)求f(x)的单调递增区间;(2)若α是第二象限角,fcoscos 2α,求cos α-sin α的值.【解析】(1)因为函数y=sin x的单调递增区间为+2kπ,,k∈Z,由-+2kπ≤3x++2kπ,k∈Z,得-≤x≤,k∈Z.所以,函数f(x)的单调递增区间为,k∈Z.(2)由已知,有sincos(cos2α-sin2α),所以sin αcos+cos αsin（cos αcos-sin αsin）(cos2α-sin2α),即sin α+cos α=(cos α-sin α)2(sin α+cos α).当sin α+cos α=0时,由α是第二象限角,知α=+2kπ,k∈Z.此时,cos α-sin α=-.当sin α+cos α≠0时,有(cos α-sin α)2=.由α是第二象限角,知cos α-sin α<0,此时cos α-sin α=-.综上所述,cos α-sin α=-或-.19.(2013·北京·文 T15)已知函数f(x)=(2cos2x-1)sin 2x+cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈,且f(α)=,求α的值.【解析】(1)因为f(x)=(2cos2x-1)sin 2x+cos 4x=cos 2xsin 2x+cos 4x=(sin 4x+cos 4x)=sin,所以f(x)的最小正周期为,最大值为.(2)因为f(α)=,所以sin=1.因为α∈,所以4α+.所以4α+.故α=.20.(2011·浙江`文T18)已知函数f(x)=Asin,x∈R,A>0,0<φ<.y=f(x)的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(1,A).(1)求f(x)的最小正周期及φ的值;(2)若点R的坐标为(1,0),∠PRQ=,求A的值.【解析】(1)由题意,得T==6.因为P(1,A)在y=Asin的图象上,所以sin=1.又因为0<φ<,所以φ=.(2)设点Q的坐标为(x0,-A).由题意可知x0+,得x0=4,所以Q(4,-A).连接PQ,在△PRQ中,∠PRQ=,由余弦定理得cos∠PRQ==-,解得A2=3.又A>0,所以A=.