北师大版八年级下册4 多边形的内角与外角和教学设计

这是一份北师大版八年级下册4 多边形的内角与外角和教学设计，共9页。教案主要包含了学情分析，教材分析，教学目标，目标叙写，学习重难点，学习方法，教学辅助，教学过程等内容，欢迎下载使用。

一、学情分析
学生的认知基础
在前一课时“多边形的内角和”的学习中，学生已经掌握了多边形的内角和公式，且在探究内角和公式的过程中进一步体会到转化、类比、从特殊到一般等数学思想的应用，所以具备了进一步本节内容的知识和方法基础.
活动经验基础 随着几何知识的深入学习，学生已经基本具备了几何问题解决的合情推理及演绎推理能力.加上八年级的学生“善于倾听、乐于分享、勇于挑战、敢于质疑”的性质特征．因此对于学习本节内容的技能条件已经成熟，学生参加探索活动的热情已经具备，所以尝试在本课中融入“独学、对学、群学”三大研学方式助力活动探索.
二、教材分析
本节内容是八年级上册多边形相关知识的延展和升华，并且在探索学习过程中又与多边形内角和、三角形外角定理等知识紧密联系、一脉相承.同时，相较七年级的几何问题探究初探，本章在问题的探究上更讲究环环相扣，层层递进；渗透类比、化归、从特殊到一般等重要的数学思想方法.在教材的编写意图上，强调“观察--发现--猜想--证明”严谨的论证过程，回归数（360°）与形（任意多边形）的完美结合.
三、教学目标（课标要求）
经历对实际情境问题的抽象，建立模型思想，了解多边形的外角、外角和概念.
经历探索多边形外角和公式的过程（观察--发现--猜想--证明），进一步发展合情推理能力及演绎推理能力，体会从特殊到一般的数学思想方法.
能运用外角和公式解决一些实际问题，感受数学的价值与魅力.
鼓励学生倾听、分享、质疑、挑战，提升数学表达能力及与人合作交流能力.
核心素养：模型思想、几何直观、推理能力、应用意识
四、目标叙写
通过探究1，经历对实际情境问题的抽象，建立模型思想，认识多边形的外角、外角和，体会学习多边形的外角和的必要性；
通过探究2，经历观察--发现--猜想--证明，获得多边形的外角和公式，体会类比、化归、从特殊到一般的数学思想方法；
通过环节3，“例题”的学习，能运用外角和公式解决问题，并体会外角和与内角和的内在关联.
五、学习重难点
重点：多边形外角和公式的探索及应用.
难点：灵活应用多边形外角和解决问题.
六、学习方法：自主、合作、探究（独学、对学、群学）；
七、教学辅助：PPT、几何画板、思维导图
八、教学过程
环节一 感受新知：问题元素-侧重数学思考
［问题情境］新闻链接：春光无限好，学子齐健身！
南山之上，涂山湖畔，众多学子正跑步健身！其中，小明同学
选择了沿一个五边形广场周围的小路，按逆时针方向跑步，满满的
朝气！引发数学爱好者提问：
（1）小明每跑完一圈，跑步方向改变的角是哪几个？它们的和是多少？
（2）如果是六边形、七边形广场呢？（问题引申）
设计意图：
创设具体的问题情境，促使学生进行学科思考（观察、直观猜想）并充分表达.同时，让生活与数学建立关联，进而体会学习本课课题的必要性所在.
本情境改编自教材的情境引入，但增加了新闻这一载体，一方面增加学生的主人翁意识，另一方面激发学生思考的兴趣.同时，在“跑步健身”中学习，渗透德育，倡导正能量.
环节二 探究新知：探究元素-侧重方法结论
探究1：多边形外角、外角和概念
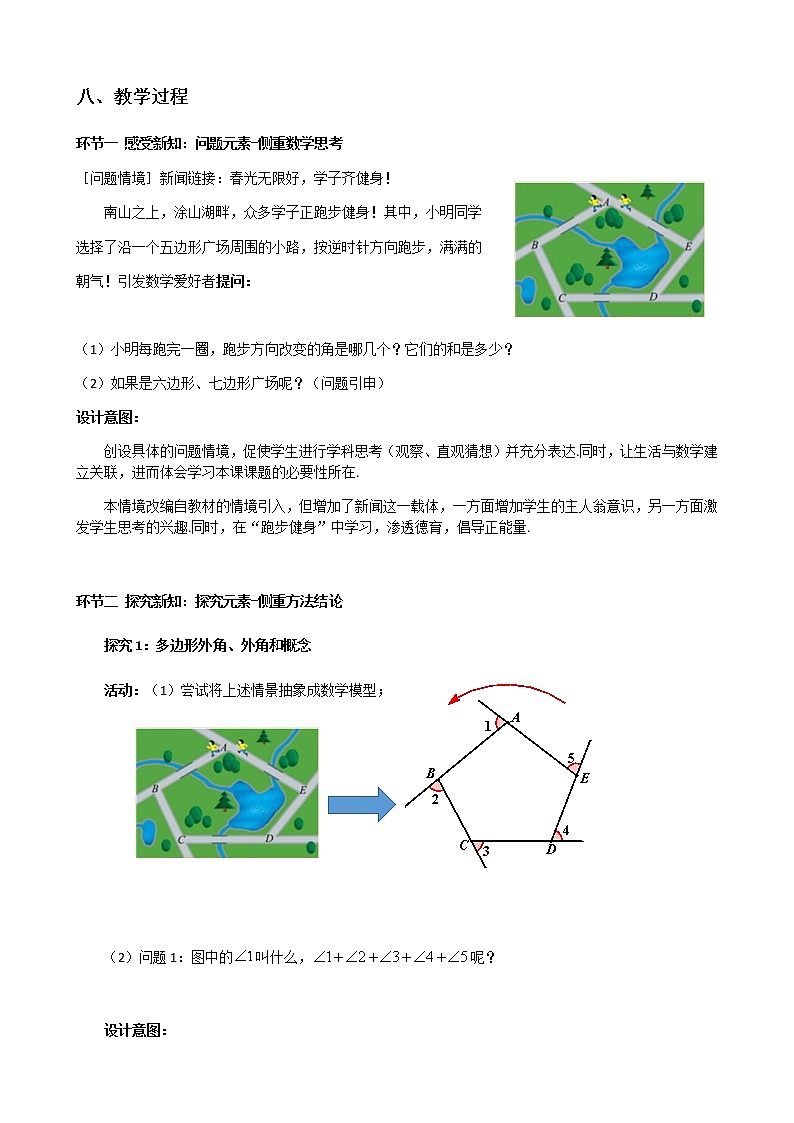
活动：（1）尝试将上述情景抽象成数学模型；
问题1：图中的叫什么，呢？
设计意图：
①引导学生将实际问题情境抽象为数学模型，运用模型思想分析并解决问题.
②学生可凭经验识别出为外角，再类比已经习得的三角形的外角概念（《八年级上 数学第七章》）得到多边形的外角概念，再回归教材，验证自己的猜想.同时，借助“形”直观认知一个项点处有2个外角，互为对顶角且外角与内角的互为邻补角关系.
③多边形外角和概念的学习，则是通过抓关键字“每个顶点处取一个外角”深化，并认识到则为五边形的外角和.进而自然揭示本课最核心的问题则是探索多边形的外角和.
探究2：多边形的外角和公式
问题2：你将如何探究多边形的外角和？
预设：生1：类比多边形的内角和探究（从特殊到一般）：

生2：利用度量、拼角等实验探究法研究；
生3：通过特殊的正多边形研究……
问题3：你对多边形的外角和有何猜想？为什么？
预设：生1：外角和为某个具体的角度；
生2：外角和会随着边数的增加，而进行一定的变化（类似于内角和）.
设计意图：
问题2旨在引导学生构建“问题探究”的框架思维，利用已有的学习经验为未知问题的探究铺路，化陌生为熟悉.
问题3则是鼓励学生对问题进行猜想，以激发后续的探究，更有目的性和针对性！
探究2.1三角形的外角和
活动1：学生借助任务单对三角形的外角和进行探究
①独立思考：形成结论；
②组内交流：探讨证明方法的多样性和科学性；
③展示质疑：全班分享、互动交流.
证明方法预设：
（1）合情推理：度量、拼角等实验探究法；
（2）演绎推理：利用多边形内角和公式计算；利用三角形的外角定理；利用过一点作平行线转移
角（构造周角）
活动2：老师利用几何画板动态展示、直观呈现三角形的外角和为360°.
探究2.2 四边形的外角和
活动3：①学生运用上述方法逐一探究四边形的外角和；
②学生问答：经历独立探究后，先由学生表达对某种证明方法
的困惑.如四边形能否利用外角定理进行证明，如何利用作平
行线进行证明？再由会的学生展示证明思路.
探究2.3 五边形的外角和
活动4：学生用最喜欢的方式探究
探究2.4 边形的外角和
学生主动生成结论： 边形的外角和为360°.
设计意图：
多边形外角和公式的探究是本课的核心之所在.
此环节的探究分纵向和横向两条线走；纵向上，从三角形到边形，遵循了从特殊到一般的探究原则，在研究主体变化过程中，学生体会到方法的迁移及外角和恒定的数字规律.横向上，对于每一个图形外角和的研究，都不拘泥于单一的方法，而是在简单图形中追求方法的全面（代数方法和几何方法，即数形结合），在复杂图形中追求方法的科学（代数法）.随着多边形边数的增加，面临着形的复杂化，应引导学生由形象思维过渡到逻辑思维，运用算理解决问题.
环节三 应用新知：应用元素-侧重如何思考
例1：（1）一个多边形的内角和等于它的外角和的4倍，它是几边形？
（2）一个正多边形的一个内角为144°，则这个正多边形的内角和为 .
例2：如图，小明从点O出发，前进后向右转24°，再前进后又向右转24°，这样一直走下去，直到他第一次回到出发点O为止，他所走的路径构成了一个多边形.
（1）小明一共走了 米；
（2）这个多边形的内角和是 度.
设计意图：
例1（1）乃教材156页的例题，旨在利用多边形内角和与外角和的数量关系建立方程解决问题；
例1（2）是“老题新做”.在学习完前一课时多边形的内角和后就遇到过此类问题，但学完外角和后，此题既可从内角和出发，又可从外角和出发，且后者更为简单.通过此题，学生可以提炼出表示正多边形的每个内角的方法：①；②
例2则是一个利用外角和解决的实际问题，让学生体会到数学来源于生活，更服务于生活的理念；同时亦能洞悉复杂生活中不变的数学原理.
环节四 梳理总结：整理元素-侧重目标错点
由学生从知识、方法、解题策略等角度自主梳理本课的收获，谈困惑；
教师利用思维导图展示本课的核心知识和方法.
设计意图：
梳理是对一堂课的回顾和反思，借助这一环节，能引导学生完善知识体系，对探究问题的思想方法有更深刻的认同.而思维导图的展示更能看到本课的框架之所在.
文化链接：内角和&外角和，谁更强大？！
欣赏来自张景中院士《数学家的眼光》的第一篇章“三角形内角和”.
在本文中，数学家陈省身否定了“三角形内角和为180°”这一看问题的
方法，而是倡导应把眼光放在外角和为360°。因为后者用一个与无关
的常数代替了与有关的公式，找到了更一般的规律！而通过蚂蚁绕圈的
方法，直观解释了“多边形的外角和为360°”这一普遍规律，随即发现
360这一数据同样适用于凸的闭曲线及凹多边形中！
同时向学生推荐课本157页习题数学理解第4题，在图形的放缩变化
中感知360°的呈现.

设计意图：
借数学家陈省身的眼光肯定了“多边形的外角和”学习的深层次意义，也深刻揭示了“数学至简，大道至简”的文化内涵.同时鼓励学生致力于事物本质规律的探究，方能洞悉“万变不离其宗”的真谛.
环节五 达标检测：评价元素-侧重达标人数
1.若一个多边形的内角和是它的外角和的3倍，则这个多边形的边数是 .
2.若一个正多边形的一个内角等于150°，则这个正多边形的内角和为 .
3.如图，在五边形ABCDE中， 为其中的三个外角，且
；BA、DE的延长线交于F点，则的度数
为 .
设计意图：
巩固在例题中所收获的知识及方法：1、2题和例1两个小题恰好一一对应，可借此评价学生一节课的听课效果和过手情况；3题重点考察学生在形上对外角及外角和的直观识别及应用.
环节六 拓展应用
新闻链接：跑步跑出“360”，点点滴滴皆学问！
据悉，学子们以“小明的五边形跑步”为载体，经历观察--发现--猜想--验证，进而得到多边形外角和恒为360°的事实。大家对此纷纷点赞！
不过，数学爱好者又提问啦！
小明跑步，先沿直线前进10米，然后左转 被称为一次转身.若五次转身后，小明恰好回到出发点，则角为多少度？
设计意图：
以“跑步情境”贯穿首尾，前后呼应！让学生充分感受到数学源于生活，归于生活的价值所在.而最后的思考题既是对外角和的应用，更是对360°的深刻解读.只有具备了数学家式的眼光，方能洞悉其中的分类讨论思想！
课后作业布置：评价元素-侧重巩固提高
必做题：教材157页习题6.8：1-4题
选做题：习题6.8：第5题
九、评价与反思
从开始构思到细细思量完成教学设计，再到应用于教学实践，是一个完整而深刻的学习过程。三点感悟，如下：
授生以“鱼”，不如授生以“渔”
在一次和科代表的对话中，我问到，“你知道多边形的外角和是多少吗？”他很骄傲地回答：“当然知道了，360°！”“那你知道怎么来的吗？”我追问道。他却垂下了头，眼睛里也失去了开始的光彩。这就是我们的教育现状，学生关注的仅仅是结果性的知识，而对过程性的知识不予理睬。长此以往，这必将使得我们丧失探究问题的习惯与能力。所以，在本课中，我想要坚持引领学生去发现、去猜想、去碰撞，直至找寻到多边形的外角和，而事实证明我们成功了。当然也有遗憾的地方：为了构建清晰的框架，问题的设置贯穿整堂课，而一堂课教学时间有限，所以在给学生留答的时间上稍显欠缺。
既入宝山，岂愿空手还
以前总觉得外角和恒为360°就是一个简单的事实。但经历了思考后，便会发现每一处的探究都可以有广度上的发散。如越是在简单的图形中，越能发现：作平行线、利用外角定理亦能得到360°，这恰恰就是论证问题的起步：发现！而寻着这条线走下去，会真正领略到360°这一恒定不变的数字规律后蕴藏着数与形的完美融合。数来自于严谨的运算，而形来自于几何直观上的认知，两者结合方能识之深刻。
德育、文化双线领航，望能走向远方
为师者总爱说数学有趣又有用，而学生看到更多接触最多的却是题。所以本课中设计了“小明跑步”这一问题情境并贯穿始终，让学生在跑步中找寻到“多边形外角和为360°”这一数学知识，同时又应用之解决跑步中的系列问题，展示了数学源于生活用于生活的价值与魅力。其次借“名人眼中的外角和”这一文化让学生看到更深刻的内涵，彰显数学的真理性及普遍性，从而有了思考上的启迪。