初中北师大版4 多边形的内角与外角和精品备课ppt课件

这是一份初中北师大版4 多边形的内角与外角和精品备课ppt课件，文件包含精选备课北师大版数学八年级下册64多边形内角和与外角和2课件ppt、精选备课北师大版数学八年级下册64多边形内角和与外角和2教案doc、精选备课北师大版数学八年级下册64多边形内角和与外角和2练习doc、精选备课北师大版数学八年级下册64多边形内角和与外角和2学案doc等4份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

1、多边形的内角和公式是什么?2、正n边形的内角怎么计算？
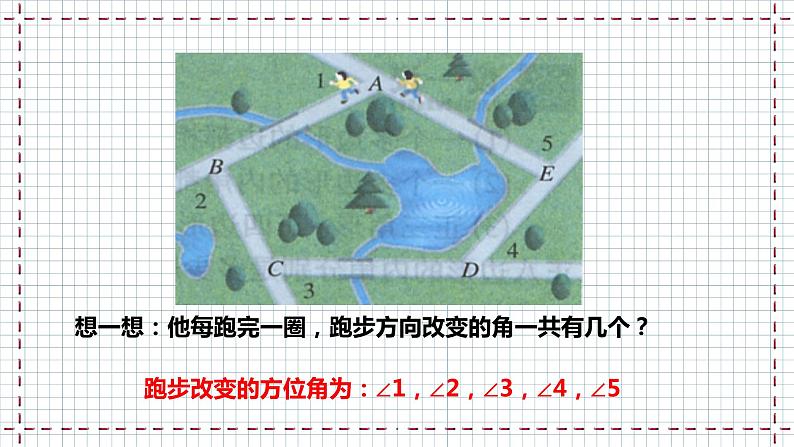
（1）小刚每从一条小路转到下一条小路时，跑步方向改变的角是哪个角？（2）他每跑完一圈，身体转过的角度之和是多少？（3）在下图中，你能求出1+2+3+4+5的结果吗？你是怎样得到的？
活动探究一：小组活动，回答下列问题。
想一想：他每跑完一圈，跑步方向改变的角一共有几个？
跑步改变的方位角为：∠1，∠2，∠3，∠4，∠5
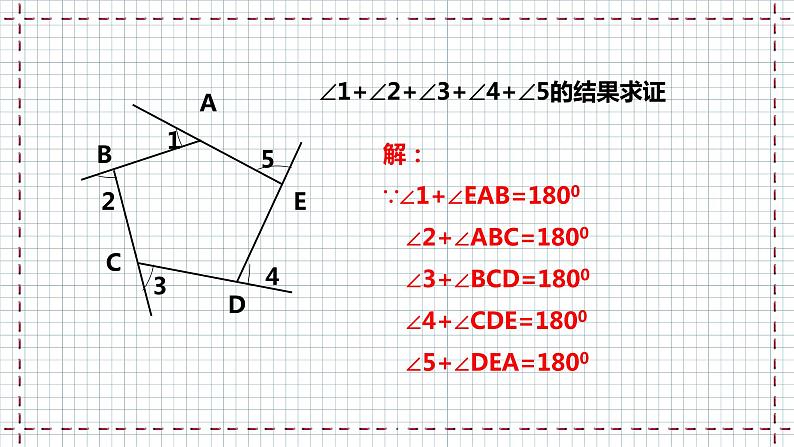
解：∵∠1+∠EAB=1800 ∠2+∠ABC=1800 ∠3+∠BCD=1800 ∠4+∠CDE=1800 ∠5+∠DEA=1800
1+2+3+4+5的结果求证
∴ ∠1+∠EAB+ ∠2+∠ABC+∠3+∠BCD+ ∠4+∠CDE+ ∠5+∠DEA=9000
∵五边形的内角和为（5-2）×1800=5400
即∠EAB+ ∠ABC+ ∠BCD+ ∠CDE+ ∠DEA=5400
∴∠1+∠2+∠3+∠4+∠5=3600
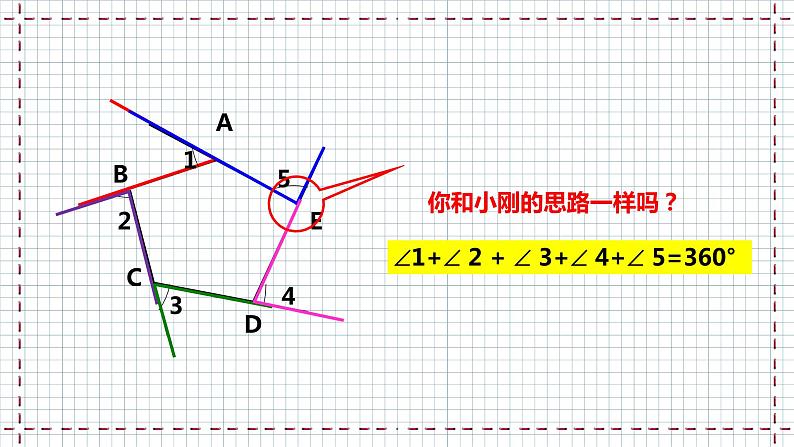
1+ 2 +  3+ 4+ 5=360°
你和小刚的思路一样吗？
如果广场的形状是六边形、八边形，那么结果会怎样？
如图，六边形的内角和为（5-2）×1800=7200∠1+∠2+∠3+∠4+∠5+∠6=6 ×1800-7200 = 3600 
观看下面动画，与同伴交流八边形呢？
定义： 多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. 在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和.
定理：多边形的外角和等于360°。
∵ n边形的每一个外角与它相邻的内角的和是_____ ∴ n边形的内角和加外角和等于 ________ ∵ n 边形的内角和等于 ___________ ∴ n 边形的外角和等于
n • 180º – (n-2) • 180º =360º
(n-2) • 180º ,
你能运用多边形内角和结论推导出多边形外角和结论吗？
注意：多边形的外角和与多边形的边数无关，它恒等于360°.
例：一个多边形的内角和等于它的外角和的3倍，它是几边形？
解：设这个多边形是n边形，则它的内角和为（n-2）﹒180°，外角和为360°。则根据题意， 得（n-2）﹒180°=3×360° 解得n=8 所以这个多边形是八边形。
变式1：下列命题是假命题的是（ ）A.三角形的内角和是180°．B.多边形的外角和都等于360°．C.五边形的内角和是900°．D.三角形的一个外角等于和它不相邻的两个内角的和．
变式2： 正五边形的每一个外角等于____，每一个内角等于_____。
变式3：一大门的栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD＝ 度．
已知一个多边形，它的内角和等于外角和的2倍，求这个多边形的边数。
解： 设多边形的边数为n ∵它的内角和等于 (n-2)•180°， 多边形外角和等于360º， ∴ (n-2)•180°=2× 360º。 解得: n=6 ∴这个多边形的边数为6
1.多边形的外角及外角和的定义多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和.2.多边形的外角和等于360°
2.若正n边形的一个内角是144度，则n=______.
1.如果十二边形的每一个内角都相等，那么每个内角是________度.
必做题：课本P156 随堂练习选做题：课本P157 习题6.8中1、2题