初中数学北师大版八年级下册1 等腰三角形课文内容课件ppt

这是一份初中数学北师大版八年级下册1 等腰三角形课文内容课件ppt，共29页。PPT课件主要包含了反证法的步骤，b是0或负数，一个也没有，至少有两个，适用反证法的题型，不都是，至少n+1个，超越梦想抢答题，达标检测等内容，欢迎下载使用。

一、情景激疑 理解领会
数学思想之： 正难则反——反证法
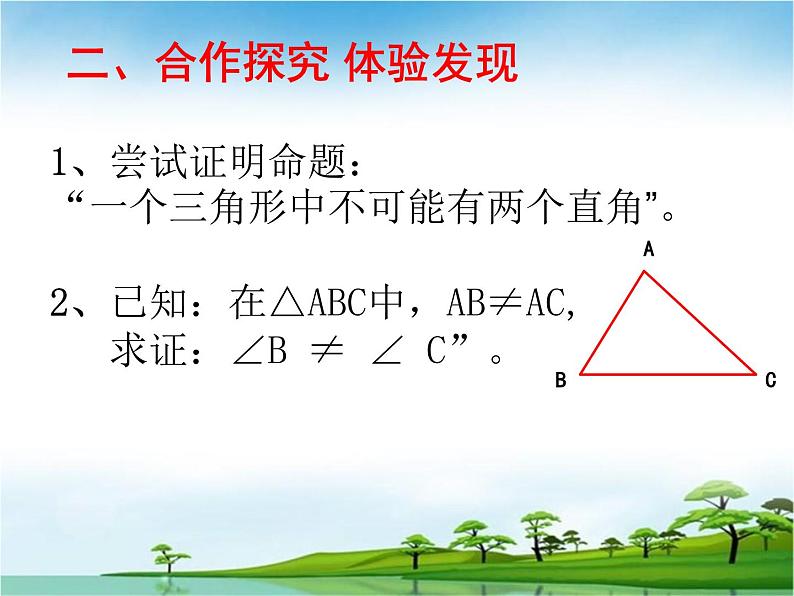
1、尝试证明命题：“一个三角形中不可能有两个直角”。
二、合作探究 体验发现
2、已知：在△ABC中，AB≠AC, 求证：∠B ≠ ∠ C”。
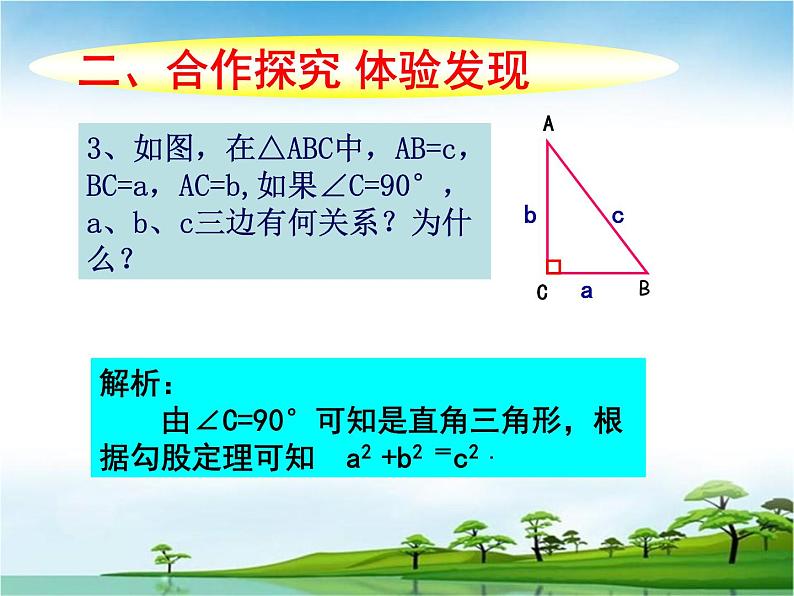
解析：　　由∠C=90°可知是直角三角形，根据勾股定理可知　a2 +b2 ＝c2 .
探究：假设a2 +b2 ＝c2，由勾股定理逆定理可知三角形ABC是直角三角形，且∠C=90°，这与已知条件∠C≠90°矛盾。假设不成立，从而说明原结论a2 +b2 ≠ c2　成立。
反证法的定义：假设命题结论的反面成立，从这个假设出发，经过推理得出与已知事实（条件、公理、定义、定理、法则、公式等）相矛盾的结果，证明结论否定不成立，间接肯定原命题的结论成立的证明方法叫做反证法。
4、你能概括出反证法的步骤吗？
①、证明命题：“一个三角形中不可能有两个直角”。
②、已知：在△ABC中，AB≠AC, 求证：∠B ≠ ∠ C”。
③、“在△ABC中，AB=c，BC=a，AC=b, ∠C≠90°，则a2 +b2 ≠ c2　”。
① 反 设： 假设命题的结论不成立，即假设结 论反面成立。② 找矛盾：从假设出发，经过正确的推理证明， 得出矛盾。③ 结 论： 由矛盾判定假设不正确，从而肯定 命题的结论正确。
练习：写出下列各结论的反面：（1）a//b（2）a≥0 （3）b是正数 ( 4 )至多有一个 （5）至少有一个
例1：已知：如图，在△ABC中,若∠C是直角， 求证：∠B一定是锐角.
证明：反设：假设结论不成立,则∠B是_____或_____
这与____________________________矛盾；
当∠B是_____时，则______________这与____________________________矛盾；
结论：综上所述,假设不成立.
∠B+ ∠C= 180°
三角形的三个内角和等于180°
∠B+ ∠C＞180°
三角形的三个内角和是180°
找矛盾：当 ∠B是_____时，则__________
三、反思提炼 加深认识
求证：在一个三角形中，至少有一个内角小于或等于60°。
已知：△ABC求证：△ABC中至少有一个内角小于或等于60°.
证明：假设　　　　　　　　　　　　　　　　　，则　　　　　　　　　　　　　　　　　　　　　。∴　　　　　　　　　　　　　　　　　　，即　　　　　　　　　　　。这与　　　　　　　　　　　矛盾．假设不成立．∴　　　　　　　　　　　　　　　　　　　　．
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C>180°
三角形的内角和为180°
△ABC中至少有一个内角小于或等于60°.
点拨：至少一个的反面是没有！
∠A+∠B+∠C>60°+60°+60°=180°
例3: 若a1、a2、a3、a4、a5都是实数，且 a1+a2+a3+a4+a5＝1试说明这五个数 中至少有一个大于或等于1/5。 证明：
假设_______________，则a1+a2+a3+a4+a5<_______________ =__与_______________________ 矛盾因此假设不成立所以_______________________________
1/5+1/5+1/5+1/5+1/5
已知条件a1+a2+a3+a4+a5=1
这5个数中至少有一个大于或等1/5
2、需分成很多类进行讨论类命题
3、结论为“至少”、“至多”、“无穷多个”类命题
4、唯一性、存在性命题
常用互为否定的表述形式：
要求：声音洪亮，表达清晰
1、说出下列命题的反面：（1）a是实数。 （2) a不大于2。
2、说出下列命题的反面：（3）至少有2个。 （4) 最多有一个。
3、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是　　　　　　　　。
4、用反证法证明“如果一个三角形没有两个相等的角，那么这个三角形不是等腰三角形”的第一步是　　　　　　　　　　　　　　　　。
5．否定结论“至多有两个解”的说法中，正确的是(　　)A．有一个解　　　　　　B．有两个解C．至少有三个解D．至少有两个解
6.命题“任意多面体的面至少有一个是三角形或四边形或五边形”的结论的否定是________．
7．梁正、赵光卓、任一杰三个人，梁 正说赵光卓撒谎，赵光卓说任一杰 撒谎，任一杰说梁正、赵光卓都撒 谎。则任一杰一定是在撒谎，你 知道为什么吗？
8、华罗庚爷爷的有趣的数学游戏。　有位老师，想辨别他的3个学生谁更聪明。他采用如下的方法：事先准备好3顶白帽子，2顶黑帽子，让他们看到，然后，叫他们闭上眼睛，分别给戴上帽子，藏起剩下的2顶帽子，最后，叫他们睁开眼，看着别人的帽子，说出自己所戴帽子的颜色。 3个学生互相看了看，都踌躇了一会，并异口同声地说出自己戴的是白帽子。
三国故事知多少？
罗巴切夫斯基 俄国数学家，非欧几何的早期发现人之一。
反证法是数学家最精当的武器之一。 ——牛顿
禁止数学家使用反证法，就像禁止拳击家使用拳头。 ——希尔伯特
反证法是数学家最有力的一件武器，比起象棋开局时以牺牲一子以取得优势的让棋法，他还要高明，象棋对弈者不外是牺牲一棋一子，数学家索性把全局拱手让给对方。 —— 哈代