2020-2021学年湖北省天门市某校初二（下）期中考试数学试卷 (2)

这是一份2020-2021学年湖北省天门市某校初二（下）期中考试数学试卷 (2)，共19页。试卷主要包含了选择题)，填空题)，解答题)等内容，欢迎下载使用。


1. 下列二次根式中属于最简二次根式的是( )
A.24B.36C.abD.a+4

2. 将下列长度的三根木棒首尾顺次连接，能构成直角三角形的是( )
A.4，5，6B.5，12，15C.1，3，2D.2，3，5

3. 若代数式1x−1+x有意义，则实数x的取值范围是( )
A.x≠1B.x≥0C.x≠0D.x≥0且x≠1

4. 下列叙述错误的是( )
A.平行四边形的对角线互相平分
B.矩形的对角线相等
C.对角线互相平分的四边形是平行四边形
D.对角线相等的四边形是矩形

5. 如图，平行四边形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点F，E，若设该平行四边形的面积为2，则图中阴影部分的面积为( )

A.4B.1C.12D.无法确定

6. 如图，在△ABC中，AB=6，AC=10，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为( )

A.8B.10C.12D.16

7. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是( )

A.2.5B.5C.322D.2

8. 如图，在矩形COED中，点D的坐标是(1, 3)，则CE的长是( )

A.3B.22C.10D.4

9. 如图，E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是( )

A.23B.12C.32D.22

10. 如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH，EH=6cm，EF=8cm，则边AB的长度等于( )

A.10cmD.8cm
二、填空题)

11. 计算−22=________.

12. 已知x=5+1，则x2−2x−3=________.

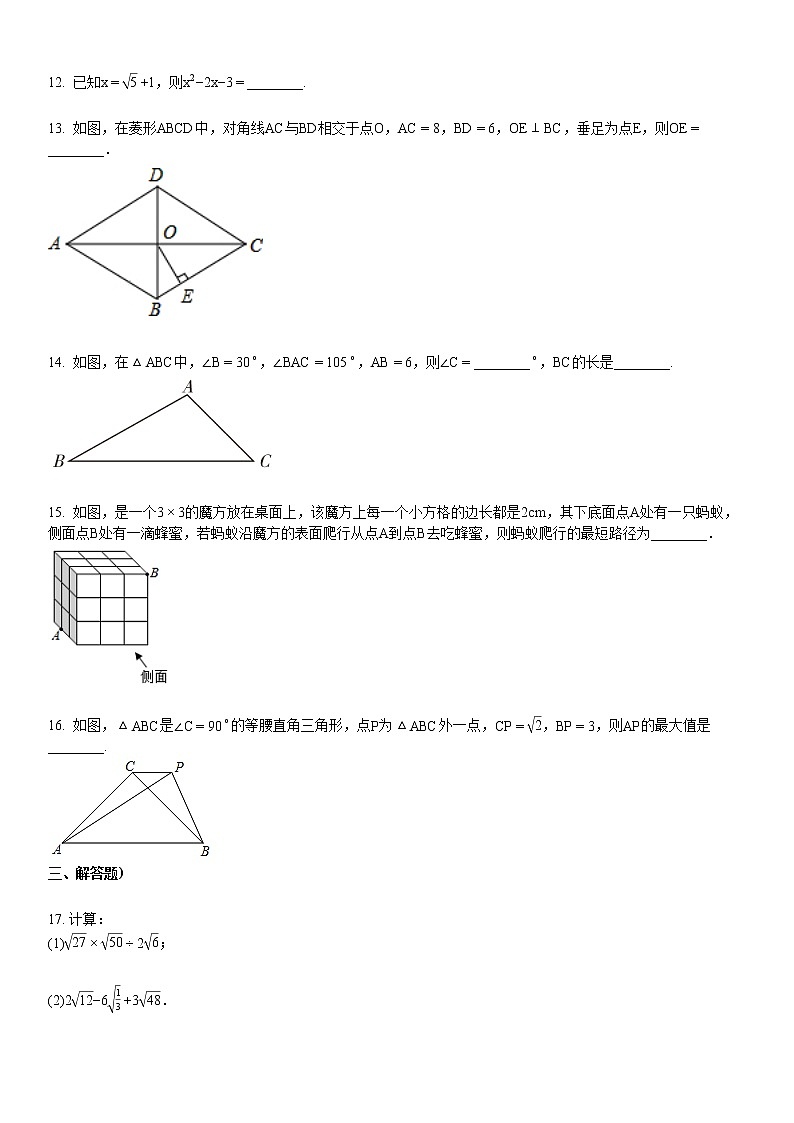
13. 如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=________．


14. 如图，在△ABC中，∠B=30∘，∠BAC=105∘，AB=6，则∠C=________​∘，BC的长是________.


15. 如图，是一个3×3的魔方放在桌面上，该魔方上每一个小方格的边长都是2cm，其下底面点A处有一只蚂蚁，侧面点B处有一滴蜂蜜，若蚂蚁沿魔方的表面爬行从点A到点B去吃蜂蜜，则蚂蚁爬行的最短路径为________．


16. 如图，△ABC是∠C=90∘的等腰直角三角形，点P为△ABC外一点，CP=2，BP=3，则AP的最大值是________.

三、解答题)

17. 计算：
(1)27×50÷26；

(2)212−613+348．

18. 已知x=2−3，求代数式x2−1x2的值．

19. 如图，方格纸中的每个小正方形的边长均为1，小正方形的顶点称为格点．已知A，B，C都是格点．

(1)小明发现∠ABC是直角，请补全他的思路；
小明的思路：
先利用勾股定理求出△ABC的三条边长，可得AB=10，BC=________，AC=________，
从而可得AB ，BC ， AC 之间的数量关系是________，
根据________，可得∠ABC 是直角；

(2)请用一种不同于小明的方法说明∠ABC是直角．

20. 如图，在正方形网格中，每个小正方形的边长都是1，每个小正方形的顶点称为格点，以格点为顶点，按下列要求用无刻度的直尺作图：

(1)在图一中作线段AB的中点M；

(2)在图二中作∠ABC的角平分线BN.

21. 如图，在▱ABCD中，E，F分别为AD，BC边的中点，连接AF，CE．求证：四边形AFCE是平行四边形．


22. 小明想知道学校旗杆的高，他发现旗杆上的绳子垂到地面还多了1m，当他把绳子的下端拉开5m后，发现下端刚好接触地面，求旗杆的高．


23. 已知：如图，矩形ABCD的对角线AC的垂直平分线EF与AD，AC，BC分别交于点E，O，F．

(1)求证：四边形AFCE是菱形；

(2)若AB=5，BC=12，EF=6，求菱形AFCE的面积．

24. 如图，▱ABCD的对角线AC、BD相交于点O，BD=12cm，AC=6cm，点E在线段BO上从点B以1cm/s的速度运动，点F在线段OD上从点O以2cm/s的速度运动．

(1)若点E、F同时运动，设运动时间为t秒，当t为何值时，四边形AECF是平行四边形．

(2)在(1)的条件下，当AB为何值时，▱AECF是菱形；

(3)求(2)中菱形AECF的面积.
参考答案与试题解析
2020-2021学年湖北省天门市某校初二（下）期中考试数学试卷
一、选择题
1.
【答案】
D
【考点】
最简二次根式
【解析】
A、B选项的被开方数中含有未开尽方的因数或因式；C选项的被开方数中含有分母；因此这三个选项都不是最简二次根式．
【解答】
解：A，24=26，不是最简二次根式，故本选项错误；
B，36=6，不是最简二次根式，故本选项错误；
C，ab=abb，不是最简二次根式，故本选项错误；
D，a+4是最简二次根式，故本选项正确.
故选D．
2.
【答案】
C
【考点】
勾股定理的逆定理
【解析】
判断是否能组成直角三角形，只要验证两小边的平方和是否等于最长边的平方即可.
【解答】
解：A，∵ 42+52≠62 ，∴不能组成直角三角形，故A选项错误；
B，∵52+122≠152 ，∴不能组成直角三角形，故B选项错误；
C，∵12+32=22 ，∴组成直角三角形，故C选项正确；
D，∵ 22+32≠52，∴不能组成直角三角形，故D选项错误.
故选C.
3.
【答案】
D
【考点】
二次根式有意义的条件
分式有意义、无意义的条件
【解析】
先根据分式及二次根式有意义的条件列出关于x的不等式组，求出x的取值范围即可．
【解答】
解：∵代数式1x − 1 + x有意义，
∴x−1≠ 0且x≥0，
解得x≥0且x≠1．
故选D.
4.
【答案】
D
【考点】
平行四边形的判定
矩形的判定与性质
【解析】
由平行四边形的判定与性质、矩形的判定与性质分别对各个选项进行判断即可．
【解答】
解：A，平行四边形的对角线互相平分，故A不符合题意；
B，矩形的对角线相等，故B不符合题意；
C，对角线互相平分的四边形是平行四边形，故C不符合题意；
D，对角线互相平分且相等的四边形是矩形，故D符合题意.
故选D．
5.
【答案】
B
【考点】
平行四边形的性质
全等三角形的性质与判定
平行四边形的面积
【解析】
根据平行四边形的性质可以证明三角形全等，进而可得阴影部分的面积为平行四边形面积的一半.
【解答】
解：∵四边形ABCD是平行四边形，
∴AB=CD，OA=OC，OB=OD.
在△AOB和△COD中，
AB=CD,OA=OC,OB=OD,
∴△AOB≅△COD(SSS)，
∴S△AOB=S△COD ，
同理可证：△AFO≅△CEO，△BOE≅△DOF，
∴ S△AFQ =S△CEO ，S△BOE =S△DOF ，
∴阴影部分的面积=S四边形ABEF=12S▱ABCD=1.
故选B.
6.
【答案】
D
【考点】
三角形中位线定理
平行四边形的性质与判定
【解析】
首先证明四边形ADEF是平行四边形，根据三角形中位线定理求出DE、EF即可解决问题．
【解答】
解：∵ BD=AD，BE=EC，
∴ DE=12AC=5，DE // AC，
∵ CF=FA，CE=BE，
∴ EF=12AB=3，EF // AB，
∴ 四边形ADEF是平行四边形，
∴ 四边形ADEF的周长=2(DE+EF)=16．
故选D．
7.
【答案】
B
【考点】
直角三角形斜边上的中线
勾股定理
【解析】
连接AC、CF，根据正方形性质求出AC、CF，∠ACD=∠GCF=45∘，再求出∠ACF=90∘，然后利用勾股定理列式求出AF，可得AH．
【解答】
解：如图，连接AC,CF，
∵ 正方形ABCD和正方形CEFG中，BC=1，CE=3，
∴ AC=2，CF=32，
∠ACD=∠GCF=45∘，
∴ ∠ACF=90∘，
由勾股定理得，AF=AC2+CF2=(2)2+(32)2=25，
∵ H是AF的中点，
∴ CH=5.
故选B．
8.
【答案】
C
【考点】
矩形的判定与性质
坐标与图形性质
【解析】
此题暂无解析
【解答】
解：∵ 四边形COED是矩形，
∴ CE=OD，
∵ 点D的坐标是(1, 3)，
∴ OD=12+32=10，
∴ CE=10.
故选C．
9.
【答案】
D
【考点】
正方形的性质
三角形的面积
【解析】
连接BP，利用面积法求解，PQ+PR的值等于C点到BE的距离，即正方形对角线的一半．
【解答】
解：如图，连接BP，过点C作CM⊥BD于点M，
∵ S△BCE =S△BPE +S△BPC
=12×BE×PR+12×BC×PQ
=12×BC×(PR+PQ)
=12×BE×CM，
∵ BC=BE，
∴ PQ+PR=CM，
∵ BE=BC=1，且正方形对角线BD=2BC=2，
又∵ BC=CD，CM⊥BD，
∴ M为BD中点，又△BDC为直角三角形，
∴ CM=12BD=22，
即PQ+PR值是22．
故选D．
10.
【答案】
B
【考点】
翻折变换（折叠问题）
矩形的性质
勾股定理
三角形的面积
【解析】
观察图形可知，边AB的长=AE+BE=2EM，根据勾股定理即可求得边HF的长，用等面积法求出HM的长即可．
【解答】
解：如图，
在△HEF中，EH=6cm，EF=8cm，
∴HF=EH2+EF2=10cm，
由折叠可知，AE=EM=BE，
∴S△EFH=12⋅EH⋅EF=12⋅HF⋅EM，
即12×6×8=12×10×EM，
解得EM=4.8，
∴AB=AE+BE=2EM=9.6cm.
故选B.
二、填空题
11.
【答案】
2
【考点】
二次根式的性质与化简
【解析】
此题暂无解析
【解答】
解：−22=4=2.
故答案为：2.
12.
【答案】
1
【考点】
二次根式的化简求值
【解析】
将x的值代入原式，再依据二次根式的混合运算顺序和运算法则计算可得．
【解答】
解：当x=5+1时，
x2−2x−3=(5+1)2−2(5+1)−3
=6+25−25−2−3
=1.
故答案为：1.
13.
【答案】
2.4
【考点】
菱形的性质
勾股定理
三角形的面积
【解析】
首先证明△BOC是直角三角形，利用面积法即12⋅CB⋅OE=12⋅OB⋅OC，即可解决问题．
【解答】
解：∵ 四边形ABCD是菱形，
∴ AC⊥BD，AO=OC=4，OD=OB=3，
∴ 在Rt△BOC中，
∵ ∠BOC=90∘，OC=4，OB=3，
∴ BC=OC2+OB2=5，
∵ OE⊥BC，
∴ 12⋅CB⋅OE=12⋅OB⋅OC，
∴ OE=OB⋅OCBC=2.4．
故答案为：2.4．
14.
【答案】
45,33+3
【考点】
含30度角的直角三角形
三角形内角和定理
勾股定理
【解析】
此题暂无解析
【解答】
解：如图，过点D作AD⊥BC交BC于点D.
∵ ∠B=30∘，∠BAC=105∘，
∴ ∠C=180∘−30∘−105∘=45∘．
∵ AD⊥BC，∴ ∠ADB=∠ADC=90∘，
∵ ∠B=30∘，AB=6，
∴ AD=12AB=3，
∴ BD=AB2−AD2=33，
∵ ∠C=45∘，
∴ DC=AD=3，
∴ BC=BD+DC=33+3．
故答案为：45；33+3．
15.
【答案】
234cm
【考点】
平面展开-最短路径问题
【解析】
如图1，把我们所看到的前面和上面组成一个平面，如图2，把我们所看到的前面和，右面组成一个平面，根据勾股定理即可得到结论．
【解答】
解：如图1，把我们所看到的前面和上面组成一个平面，
AB=42+6+62=410cm；
如图2，把我们所看到的前面和右面组成一个平面，
AB=4+62+62=234cm，
∵ 410>234，
∴ 蚂蚁爬行的最短路径为234cm.
故答案为：234cm.
16.
【答案】
5
【考点】
等腰直角三角形
全等三角形的性质与判定
【解析】
此题暂无解析
【解答】
解：如图，过点C作CQ⊥CP，且CQ=CP，连接AQ，PQ.
∵ ∠ACQ+∠BCQ=∠BCP+∠BCQ=90∘，
∴ ∠ACQ=∠BCP，
在△ACQ和△BCP中，∵ AC=BC,∠ACQ=∠BCP,CQ=CP,
∴ △ACQ≅△BCP(SAS)，
∴ AQ=BP=3，CQ=CP=2，
∴ PQ=CQ2+CP2=2,
∴ AP≤AQ+PQ=3+2=5，
即AP的最大值是5.
故答案为：5．
三、解答题
17.
【答案】
解：(1)原式=33×52÷26
=156÷26
=152.
(2)原式=43−23+123=143．
【考点】
二次根式的混合运算
【解析】
（1）先把二次根式化为最简二次根式，然后进行二次根式的乘除运算；
（2）先把二次根式化为最简二次根式，然后合并即可．
【解答】
解：(1)原式=33×52÷26
=156÷26
=152.
(2)原式=43−23+123=143．
18.
【答案】
解：当x=2−3时，
x2−1x2=(2−3)2−1(2−3)2
=7−43−17−43
=7−43−(7+43)
=−83．
【考点】
列代数式求值
二次根式的化简求值
【解析】
此题暂无解析
【解答】
解：当x=2−3时，
x2−1x2=(2−3)2−1(2−3)2
=7−43−17−43
=7−43−(7+43)
=−83．
19.
【答案】
10,25,AB2+BC2=AC2,勾股定理的逆定理
(2)过A点作AD⊥BE于D，过C作CE⊥DB于E，
由图可知： AD=BE， BD=CE，∠ADB=∠BEC=90∘，
在△ADB和△BEC中，AD=BE,∠ADB=∠BEC,BD=CE,
∴ △ADB≅△BECSAS，
∴ ∠ABD=∠BCE.
在△BEC中， ∠BEC+∠BCE+∠EBC=180∘，
∴ ∠BCE+∠EBC=180∘−∠BEC=90∘，
∴ ∠ABD+∠EBC=90∘，
∵ D，B，E三点共线，
∴ ∠ABD+∠EBC+∠ABC=180∘，
∴ ∠ABC=180∘−∠ABD+∠EBC=90∘.
【考点】
勾股定理
勾股定理的逆定理
全等三角形的性质与判定
【解析】
(1)根据勾股定理和勾股定理的逆定理解答即可；
(2)根据全等三角形的判定和性质解答即可．
【解答】
解：(1)∵AB=12+32=10， BC=12+32=10，AC=22+42=25，
∴ AB2+BC2=AC2，
根据勾股定理的逆定理可知：△ABC是直角三角形，
∴ ∠ABC=90∘.
故答案为：10；25；AB2+BC2=AC2；勾股定理的逆定理.
(2)过A点作AD⊥BE于D，过C作CE⊥DB于E，
由图可知： AD=BE， BD=CE，∠ADB=∠BEC=90∘，
在△ADB和△BEC中，AD=BE,∠ADB=∠BEC,BD=CE,
∴ △ADB≅△BECSAS，
∴ ∠ABD=∠BCE.
在△BEC中， ∠BEC+∠BCE+∠EBC=180∘，
∴ ∠BCE+∠EBC=180∘−∠BEC=90∘，
∴ ∠ABD+∠EBC=90∘，
∵ D，B，E三点共线，
∴ ∠ABD+∠EBC+∠ABC=180∘，
∴ ∠ABC=180∘−∠ABD+∠EBC=90∘.
20.
【答案】
解：(1)如图所示即为所求线段AB的中点M.
(2)如图所示即为所求∠ABC的角平分线BN.
【考点】
作图—复杂作图
作角的平分线
【解析】
此题暂无解析
【解答】
解：(1)如图所示即为所求线段AB的中点M.
(2)如图所示即为所求∠ABC的角平分线BN.
21.
【答案】
证明：∵ 四边形ABCD是平行四边形，
∴ AD=BC，AD // BC，
∵ E，F分别为AD，BC边的中点，
∴ AE=12AD，CF=12BC，AE // CF，
∴ AE=CF，
∴ 四边形AFCE是平行四边形．
【考点】
平行四边形的性质与判定
【解析】
由平行四边形的性质得出AD＝BC，AD // BC，证出AE＝CF，即可得出四边形AFCE是平行四边形．
【解答】
证明：∵ 四边形ABCD是平行四边形，
∴ AD=BC，AD // BC，
∵ E，F分别为AD，BC边的中点，
∴ AE=12AD，CF=12BC，AE // CF，
∴ AE=CF，
∴ 四边形AFCE是平行四边形．
22.
【答案】
解：设旗杆的高AB为xm，则绳子AC的长为(x+1)m.
在Rt△ABC中，AB2+BC2=AC2，
∴ x2+52=(x+1)2，
解得x=12，
∴ AB=12，
答：旗杆高12m．
【考点】
勾股定理的应用
勾股定理
勾股定理的综合与创新
【解析】
解：设旗杆的高AB为xm，则绳子AC的长为(x+1)m.
在Rt△ABC中，AB2+BC2=AC2，
∴ x2+52=(x+1)2，
解得x=12，
∴ AB=12，
答：旗杆高12m．
【解答】
根据题意设旗杆的高AB为xm，则绳子AC的长为(x+1)m，再利用勾股定理即可求得AB的长，即旗杆的高．
23.
【答案】
解：(1)∵ 四边形ABCD是矩形，
∴ AE // FC，
∴ ∠EAO=∠FCO，
∵ EF垂直平分AC，
∴ AO=CO，FE⊥AC，
又∠AOE=∠COF，
∴ △AOE≅△COF，
∴ EO=FO，
∴ 四边形AFCE为平行四边形，
又∵ FE⊥AC，
∴ 平行四边形AFCE为菱形.
(2)在Rt△ABC中，由AB=5，BC=12，
根据勾股定理，得AC=AB2+BC2=52+122=13，
又∵ EF=6，
∴ 菱形AFCE的面积S=12AC⋅EF=12×13×6=39．
【考点】
矩形的性质
全等三角形的性质与判定
菱形的判定
勾股定理
菱形的面积
【解析】
（1）根据ABCD为矩形，根据矩形的对边平行得到AE与CF平行，由两直线平行得到一对内错角相等，又EF垂直平分AC，根据垂直平分线的定义得到AO=CO，且AC与EF垂直，再加上一对对顶角相等，利用“ASA”得到三角形AOE与三角形COF全等，根据全等三角形的对应边相等得到AE=FC，由一组对边平行且相等的四边形为平行四边形得到AFCE为平行四边形，又根据对角线垂直的平行四边形为菱形即可得证；
（2）由矩形的性质得到∠B为直角，在直角三角形ABC中，由AB与BC的长，利用勾股定理求出AC的长，又已知EF的长，而AC与EF为菱形AFCE的两条对角线，根据对角线乘积的一半即可求出菱形的面积．
【解答】
解：(1)∵ 四边形ABCD是矩形，
∴ AE // FC，
∴ ∠EAO=∠FCO，
∵ EF垂直平分AC，
∴ AO=CO，FE⊥AC，
又∠AOE=∠COF，
∴ △AOE≅△COF，
∴ EO=FO，
∴ 四边形AFCE为平行四边形，
又∵ FE⊥AC，
∴ 平行四边形AFCE为菱形.
(2)在Rt△ABC中，由AB=5，BC=12，
根据勾股定理，得AC=AB2+BC2=52+122=13，
又∵ EF=6，
∴ 菱形AFCE的面积S=12AC⋅EF=12×13×6=39．
24.
【答案】
解：(1)若四边形AECF为平行四边形，
∴ AO=OC，EO=OF，
∵ 四边形ABCD为平行四边形，
∴ BO=OD=6cm，
∴ EO=6−t，OF=2t，
∴ 6−t=2t，
∴ t=2s，
∴ 当t为2秒时，四边形AECF是平行四边形；
(2)若四边形AECF是菱形，
∴ AC⊥BD，
∴ AO2+BO2=AB2，
∴ AB=36+9=35cm，
∴ 当AB为35cm时，▱AECF是菱形.
(3)∵ 四边形AECF是菱形，
∴ BO⊥AC，OE=OF，
∵ 四边形ABCD是平行四边形，
∴ BO=OD，
∴ BE=DF，
∴ t=6−2t，
∴ t=2，
∴ BE=DF=2cm，
∴ EF=8cm，
∴ 菱形AECF的面积=12AC⋅EF=12×6×8=24cm2.
【考点】
菱形的面积
菱形的判定
平行四边形的判定
【解析】
（1）若是平行四边形，所以BD=12cm，则B0=DO=6cm，故有6−1t=2t，即可求得t值；
（2）①若是菱形，则AC垂直于BD，即有AO2+BO2=AB2，故AB可求；
②若是矩形，EF=AC，则此时E在O上，所以四边形AECF不可以是矩形．
【解答】
解：(1)若四边形AECF为平行四边形，
∴ AO=OC，EO=OF，
∵ 四边形ABCD为平行四边形，
∴ BO=OD=6cm，
∴ EO=6−t，OF=2t，
∴ 6−t=2t，
∴ t=2s，
∴ 当t为2秒时，四边形AECF是平行四边形；
(2)若四边形AECF是菱形，
∴ AC⊥BD，
∴ AO2+BO2=AB2，
∴ AB=36+9=35cm，
∴ 当AB为35cm时，▱AECF是菱形.
(3)∵ 四边形AECF是菱形，
∴ BO⊥AC，OE=OF，
∵ 四边形ABCD是平行四边形，
∴ BO=OD，
∴ BE=DF，
∴ t=6−2t，
∴ t=2，
∴ BE=DF=2cm，
∴ EF=8cm，
∴ 菱形AECF的面积=12AC⋅EF=12×6×8=24cm2.