2022年中考数学二轮专题复习《压轴题-二次函数》专项复习(2份，教师版+原卷版)

这是一份2022年中考数学二轮专题复习《压轴题-二次函数》专项复习(2份，教师版+原卷版)，文件包含2022年中考数学二轮专题复习《压轴题-二次函数》专项复习教师版doc、2022年中考数学二轮专题复习《压轴题-二次函数》专项复习原卷版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

如图，⊙E的圆心E（3，0），半径为5，⊙E与y轴相交于A、B两点（点A在点B的上方），与x轴的正半轴交于点C，直线l的解析式为y=eq \f(3,4)x+4，与x轴相交于点D，以点C为顶点的抛物线过点B．
（1）求抛物线的解析式；
（2）判断直线l与⊙E的位置关系，并说明理由；
（3）动点P在抛物线上，当点P到直线l的距离最小时．求出点P的坐标及最小距离．
【答案解析】解：（1）如图1，连接AE，由已知得：AE=CE=5，OE=3，
在Rt△AOE中，由勾股定理得，OA=4，
∵OC⊥AB，∴由垂径定理得，OB=OA=4，OC=OE+CE=3+5=8，
∴A（0，4），B（0，﹣4），C（8，0），
∵抛物线的定点为C，
∴设抛物线的解析式为y=a(x-8)2，
将点B的坐标代入上解析的式，得64a=﹣4，
故a=，∴，
∴所求抛物线的解析式为：；
（2）在直线l的解析式y=eq \f(3,4)x+4中，令y=0，得eq \f(3,4)x+4=0，解得x=，
∴点D的坐标为（，0），当x=0时，y=4，
∴点A在直线l上，在Rt△AOE和Rt△DOA中，
∵，，∴，
∵∠AOE=∠DOA=90°，∴△AOE∽△DOA，∴∠AEO=∠DAO，
∵∠AEO+∠EAO=90°，∴∠DAO+∠EAO=90°，即∠DAE=90°，
因此，直线l与⊙E相切与A；
（3）如图2，过点P作直线l的垂线段PQ，垂足为Q，过点P作直线PM垂直于x轴，
交直线l于点M．设M（m，eq \f(3,4)m+4），P（m，），则PM===，
当m=2时，PM取得最小值6.2，此时，P（2，-2.25），对于△PQM，
∵PM⊥x轴，∴∠QMP=∠DAO=∠AEO，
又∠PQM=90°，∴△PQM的三个内角固定不变，
∴在动点P运动的过程中，△PQM的三边的比例关系不变，
∴当PM取得最小值时，PQ也取得最小值，
PQ最小=PM最小•sin∠QMP=PM最小•sin∠AEO=6.2，
∴当抛物线上的动点P的坐标为（2，-2.25）时，点P到直线l的距离最小，
其最小距离为6.2．
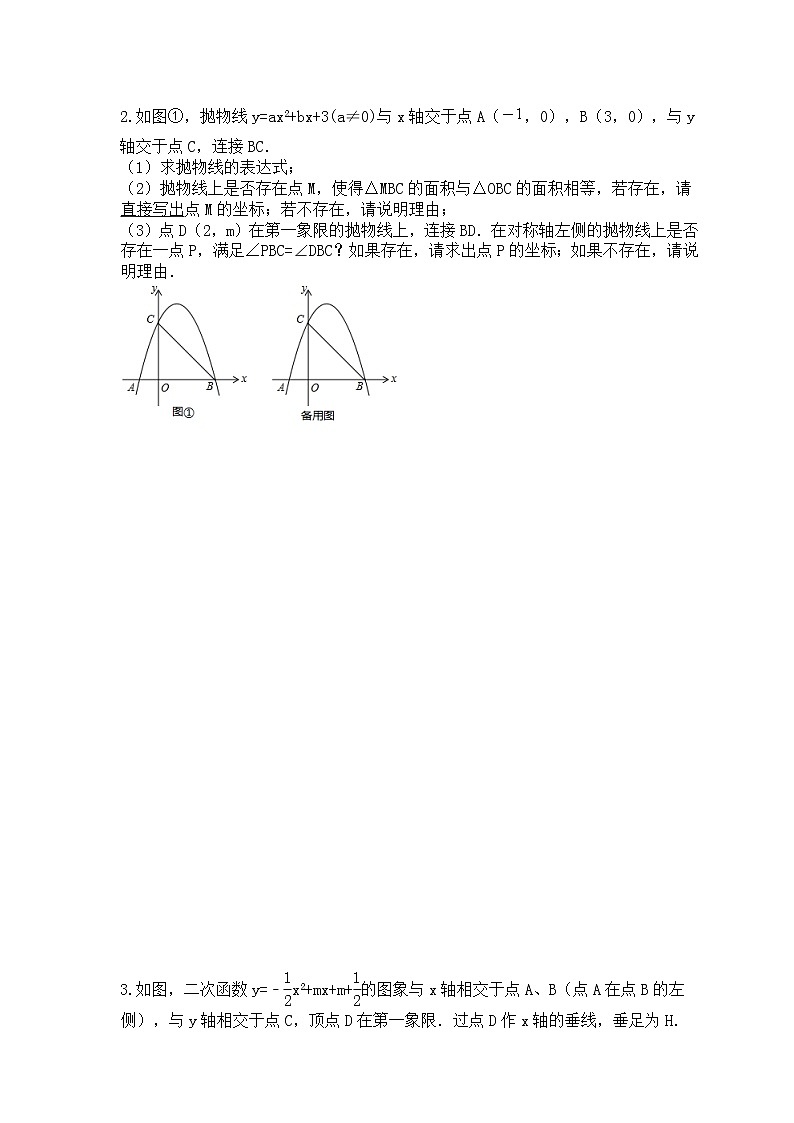
如图①，抛物线y=ax2+bx+3(a≠0)与x轴交于点A（，0），B（3，0），与y轴交于点C，连接BC．
（1）求抛物线的表达式；
（2）抛物线上是否存在点M，使得△MBC的面积与△OBC的面积相等，若存在，请直接写出点M的坐标；若不存在，请说明理由；
（3）点D（2，m）在第一象限的抛物线上，连接BD．在对称轴左侧的抛物线上是否存在一点P，满足∠PBC=∠DBC？如果存在，请求出点P的坐标；如果不存在，请说明理由．


【答案解析】解：（1）∵抛物线y=ax2+bx+3与x轴交于点A（-1，0），B（3，0），
，解得，
∴抛物线的表达式为．
（2）存在．M1（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ），M2（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）
（3）存在．如图，设BP交轴y于点G．
∵点D（2，m）在第一象限的抛物线上，
∴当x=2时，m=3．
∴点D的坐标为（2，3）．
把x=0代入y=-x2+2x+3，得y=3．
∴点C的坐标为（0，3）．
∴CD∥x轴，CD = 2．
∵点B（3，0），∴OB=OC=3
∴∠OBC=∠OCB=45°．
∴∠DCB=∠OBC=∠OCB=45°，
又∵∠PBC=∠DBC，BC=BC，
∴△CGB ≌ △CDB（ASA），∴CG=CD=2．
∴OG=OCCG=1，∴点G的坐标为（0，1）．
设直线BP的解析式为y=kx+1，将B（3，0）代入，得3k+1=0，解得k=- eq \f(1,3)．
∴直线BP的解析式为y=- eq \f(1,3)x+1.
令- eq \f(1,3)x+1=-x2+2x+3．解得x1=-eq \f(2,3)，x2=3．
∵点P是抛物线对称轴x=1左侧的一点，即x<1，∴x=-eq \f(2,3)．
把x=-eq \f(2,3)代入抛物线y=-x2+2x+3中，解得y= SKIPIF 1 < 0 .
∴当点P的坐标为（-eq \f(2,3)， SKIPIF 1 < 0 ）时，满足∠PBC=∠DBC．
如图，二次函数y=﹣eq \f(1,2)x2+mx+m+eq \f(1,2)的图象与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，顶点D在第一象限．过点D作x轴的垂线，垂足为H．
（1）当m=eq \f(3,2)时，求tan∠ADH的值；
（2）当60°≤∠ADB≤90°时，求m的变化范围；
（3）设△BCD和△ABC的面积分别为S1、S2，且满足S1=S2，求点D到直线BC的距离．
【答案解析】解：（1）∵当m=时，y=﹣x2+x+2=﹣（x﹣）2+ SKIPIF 1 < 0 ，
∴顶点D（， SKIPIF 1 < 0 ），与x轴的交点A（﹣1，0），B（4，0），
∴DH= SKIPIF 1 < 0 ，AH=﹣（﹣1）=1，∴tan∠ADH=eq \f(4,5)；
（2）y=﹣x2+mx+m+=﹣（x﹣m）2+ SKIPIF 1 < 0 ，∴顶点D（m， SKIPIF 1 < 0 ），
令y=﹣x2+mx+m+=0，解得：x=﹣1或2m+1
则与x轴的交点A（﹣1，0），B（2m+1，0），
∴DH= SKIPIF 1 < 0 ，AH=m﹣（﹣1）=m+1，∴tan∠ADH= SKIPIF 1 < 0 ．
当60°≤∠ADB≤90°时，由对称性得30°≤∠ADH≤45°，
∴当∠ADH=30°时， SKIPIF 1 < 0 =eq \f(\r(3),3)，∴m=2eq \r(3)﹣1，
当∠ADH=45°时， SKIPIF 1 < 0 =1，∴m=1，∴1≤m≤2eq \r(3)﹣1；
（3）设DH与BC交于点M，则点M的横坐标为m．
设过点B（2m+1，0），C（0，m+）的直线解析式为；y=kx+b，
则，解得，即y=﹣eq \f(1,2)x+m+eq \f(1,2)．
当x=m时，y=﹣m+m+= SKIPIF 1 < 0 ，∴M（m， SKIPIF 1 < 0 ）．
∴DM=﹣=，AB=（2m+1）﹣（﹣1）=2m+2，
又，∵S△DBC=S△ABC，∴•（2m+1）=（2m+2）•（m+），
又∵抛物线的顶点D在第一象限，∴m＞0，解得m=2．
当m=2时，A（﹣1，0），B（5，0），C（0，），
∴BC==，∴S△ABC=×6×=．
设点D到直线BC的距离为d．∵S△DBC=BC•d，
∴וd=，∴d=．
如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．
（1）如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；
①求此抛物线的解析式；
②由条件可知点D的坐标是（0，4），若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；
（2）如图2，若a=1，求证：无论b，c取何值，点D均为定点，并求出该定点坐标．
【答案解析】解：（1）①∵抛物线y=ax2+bx+c过点A（﹣2，0），B（8，0），C（0，﹣4），
∴，解得．
∴抛物线的解析式为：y=eq \f(1,4)x2﹣eq \f(3,2)x﹣4；
②设直线BD的解析式为y=kx+b，∵B（8，0），D（0，4），
∴，解得，
∴直线BD解析式为：y=﹣eq \f(1,2)x+4．设M（x，eq \f(1,4)x2﹣eq \f(3,2)x﹣4），
如图1，过点M作ME∥y轴，交BD于点E，则E（x，﹣eq \f(1,2)x+4）．
∴ME=（﹣eq \f(1,2)x+4）﹣（eq \f(1,4)x2﹣eq \f(3,2)x﹣4）=﹣eq \f(1,4)x2+x+8．
∴S△BDM=S△MED+S△MEB=eq \f(1,2)ME（xE﹣xD）+eq \f(1,2)ME（xB﹣xD）=eq \f(1,2)ME（xB﹣xD）=4ME，
∴S△BDM=4（﹣eq \f(1,4)x2+x+8）=﹣x2+4x+32=﹣（x﹣2）2+36．
∴当x=2时，△BDM的面积有最大值为36；
（2）如图2，连接AD、BC．
由圆周角定理得：∠ADO=∠CBO，∠DAO=∠BCO，
∴△AOD∽△COB，∴=，
设A（x1，0），B（x2，0），
∵已知抛物线y=x2+bx+c（c＜0），
∵OC=﹣c，OA=﹣x1=﹣，OB=x2=，
∴=，且x1x2=•==c，
∴OD==1，
∴无论b，c取何值，点D均为定点，该定点坐标D（0，1）．
如图，已知在平面直角坐标系中，直线y=- eq \f(3,4)x+6与x轴、y轴的交点分别为A、B，将∠OBA对折，使点O的对应点H落在直线AB上，折痕交x轴于点C．
（1）直接写出点C的坐标，并求过A、B、C三点的抛物线的解析式；
（2）若抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四边形？若存在，求出点P的坐标；若不存在，说明理由；
（3）设抛物线的对称轴与直线BC的交点为T，Q为线段BT上一点，直接写出|QA﹣QO|的取值范围．
【答案解析】解：（1）点C的坐标为（3，0）．
∵点A、B的坐标分别为A（8，0），B（0，6），
∴可设过A、B、C三点的抛物线的解析式为y=a（x﹣3）（x﹣8）．
将x=0，y=6代入抛物线的解析式，得a=eq \f(1,4)．
∴过A、B、C三点的抛物线的解析式为y=eq \f(1,4)x2- SKIPIF 1 < 0 x+6．
（2）可得抛物线的对称轴为直线x=5.5，顶点D的坐标为(5.5,- SKIPIF 1 < 0 )，
设抛物线的对称轴与x轴的交点为G．
直线BC的解析式为y=﹣2x+6.
如图，取OA的中点E，作点D关于点E的对称点P，作PN⊥x轴于点N．
则∠PEN=∠DEG，∠PNE=∠DGE，PE=DE．
可得△PEN≌△DEG．
由OE=4，可得E点的坐标为（4，0）．
NE=EG=eq \f(3,2)，ON=OE﹣NE=eq \f(5,2)，NP=DG= SKIPIF 1 < 0 ．∴点P的坐标为(eq \f(5,2), SKIPIF 1 < 0 )．
∵x=eq \f(5,2) 时，-2x+6≠ SKIPIF 1 < 0 ， ∴点P不在直线BC上．
∴直线BC上不存在符合条件的点P．
（3）|QA﹣QO|的取值范围是0≤|QA-QO|≤4．
当Q在OA的垂直平分线上与直线BC的交点时，（如点K处），
此时OK=AK，则|QA﹣QO|=0，
当Q在AH的延长线与直线BC交点时，此时|QA﹣QO|最大，
直线AH的解析式为：y=﹣eq \f(3,4)x+6，直线BC的解析式为：y=﹣2x+6，
联立可得：交点为（0，6），∴OQ=6，AQ=10，∴|QA﹣QO|=4，
∴|QA﹣QO|的取值范围是：0≤|QA﹣QO|≤4．
抛物线y=-x2+bx+c经过点A、B、C，已知A（-1，0），C（0，3）．
（1）求抛物线的解析式；
（2）如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；
（3）如图2，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，请指出实数m的变化范围，并说明理由．
【答案解析】解：（1）由题意得：b=2,c=3，
∴抛物线解析式为y=-x2+2x+3；
（2）令-x2+2x+3=0，∴x1= -1，x2=3，即B（3，0），
设直线BC的解析式为y=kx+b′，
得k=-1,b’=3，∴直线BC的解析式为y=-x+3，
设P（a，3-a），则D（a，-a2+2a+3），∴PD=（-a2+2a+3）-（3-a）=-a2+3a，
∴S△BDC=S△PDC+S△PDB= SKIPIF 1 < 0
∴当a=eq \f(3,2)时，△BDC的面积最大，此时P（eq \f(3,2)，eq \f(3,2)）；
（3）由（1），y=-x2+2x+3=-（x-1）2+4，∴OF=1，EF=4，OC=3，
过C作CH⊥EF于H点，则CH=EH=1，
当M在EF左侧时，∵∠MNC=90°，则△MNF∽△NCH，∴ SKIPIF 1 < 0 ，
设FN=n，则NH=3-n，∴ SKIPIF 1 < 0 ，即n2-3n-m+1=0，
关于n的方程有解，△=（-3）2-4（-m+1）≥0，得m≥-1.25，
当M在EF右侧时，Rt△CHE中，CH=EH=1，∠CEH=45°，即∠CEF=45°，
作EM⊥CE交x轴于点M，则∠FEM=45°，∵FM=EF=4，∴OM=5，
即N为点E时，OM=5，∴m≤5，
综上，m的变化范围为：1.25≤m≤5．
如图,在直角坐标系中放入一边长OC为6的矩形纸片ABCO，将纸翻折后，使点B恰好落在x轴上，记为B’，折痕为CE，已知tan∠OB/C=eq \f(3,4).
（1）求B’点的坐标；
（2）求折痕CE所在的直线的解析式；
（3）作B’G//AB交CE于G，已知抛物线通过点G，以O为圆心OG的长为半径的圆与抛物线是否还有除G点以外的交点？若有，请找出这个交点坐标。
【答案解析】解：（1）在Rt△B'OC中，，
DC=6，∴OB'=8，点B'（8，0），
（2）由已知得：△CBE∽△C B'E，∴BE=B'E，CB'=CB=OA，

设AE=n，则EB'=EB=b-n，AB'=AO-OB'=10-8=2
∴，得，∴，
设直线CE的解析式y=kx+b，
根据题意得 解得：
CE所在直线的解析式y=- eq \f(1,3)x+6
（3）设G(8,a)，∵点G在直线CE上，a= eq \f(10,3)
∴G(8,eq \f(10,3))
以O点为圆心，以OG为半径的圆的对称轴是轴，
抛物线的对称轴也是y轴。
∴除交点G外，另有交点H，H是G点关于y轴的对称点．
其坐标为(-8,1.25)
如图，经过点A(0，－4)的抛物线y=eq \f(1,2)x2＋bx＋c与x轴相交于点B(－0，0)和C，O为坐标原点．
(1)求抛物线的解析式；
(2)将抛物线y=eq \f(1,2)x2＋bx＋c向上平移eq \f(7,2)个单位长度、再向左平移m(m＞0)个单位长度，得到新抛物线．若新抛物线的顶点P在△ABC内，求m的取值范围；
(3)设点M在y轴上，∠OMB＋∠OAB=∠ACB，求AM的长．
【答案解析】解：（1）将A（0，-4）、B（-2，0）代入抛物线y=eq \f(1,2)x2+bx+c中，得：
解得：b=-1 c=-4
∴抛物线的解析式：y=eq \f(1,2)x2-x-4．
（2）由题意，新抛物线的解析式可表示为：y=eq \f(1,2)（x+m）2-（x+m）-4+7/2 ，
它的顶点坐标P：（1-m，-1）；
由（1）的抛物线解析式可得：C（4，0）；
那么直线AB：y=-2x-4；直线AC：y=x-4；
当点P在直线AB上时，-2（1-m）-4=-1，解得：m=5 2 ；
当点P在直线AC上时，（1-m）-4=-1，解得：m=-2；
∴当点P在△ABC内时，-2＜m＜5/2 ；
又∵m＞0，
∴符合条件的m的取值范围：0＜m＜5/2 ．
（3）由A（0，-4）、B（4，0）得：OA=OC=4，且△OAC是等腰直角三角形；
如图，在OA上取ON=OB=2，则∠ONB=∠ACB=45°；
∴∠ONB=∠NBA+OAB=∠ACB=∠OMB+∠OAB，即∠ONB=∠OMB；
如图，在△ABN、△AM1B中，∠BAN=∠M1AB，∠ABN=∠AM1B，
∴△ABN∽△AM1B，得：AB2=AN•AM1；
易得：AB2=（-2）2+42=20，AN=OA-ON=4-2=2；
∴AM1=20÷2=10，OM1=AM1-OA=10-4=6；
而∠BM1A=∠BM2A=∠ABN，
∴OM1=OM2=6，AM2=OM2-OA=6-4=2．
综上，AM的长为6或2．
如图1，已知直线y=kx与抛物线y= SKIPIF 1 < 0 x2+ SKIPIF 1 < 0 交于点A（3，6）．
（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？
【答案解析】解：（1）把点A（3，6）代入y=kx 得
∵6=3k，∴k=2，
∴y=2x．OA=3eq \r(5)．
（2） SKIPIF 1 < 0 是一个定值，理由如下：
如答图1，过点Q作QG⊥y轴于点G，QH⊥x轴于点H．
①当QH与QM重合时，显然QG与QN重合，
此时 SKIPIF 1 < 0 =tan∠AOM=2；
②当QH与QM不重合时，
∵QN⊥QM，QG⊥QH
不妨设点H，G分别在x、y轴的正半轴上，
∴∠MQH=∠GQN，
又∵∠QHM=∠QGN=90°
∴△QHM∽△QGN，
∴ SKIPIF 1 < 0 =tan∠AOM=2；
当点P、Q在抛物线和直线上不同位置时，同理可得 SKIPIF 1 < 0 =2．
（3）如图2，延长AB交x轴于点F，过点F作FC⊥OA于点C，过点A作AR⊥x轴于点R
∵∠AOD=∠BAE，
∴AF=OF，
∴OC=AC=eq \f(1,2)OA=eq \f(3,2)eq \r(5)
∵∠ARO=∠FCO=90°，∠AOR=∠FOC，
∴△AOR∽△FOC，
∴，∴OF=，
∴点F（7.5，0），设点B（x，），
过点B作BK⊥AR于点K，则△AKB∽△ARF，
∴，即，解得x1=6，x2=3（舍去），
∴点B（6，2），∴BK=6﹣3=3，AK=6﹣2=4，
∴AB=5 ；
设直线AF为y=kx+b（k≠0）把点A（3，6），点F（7.5，0）代入得
k=- eq \f(4,3)，b=10，∴y=- eq \f(4,3)x+10，
∴，∴（舍去），，∴B（6，2），∴AB=5
在△ABE与△OED中
∵∠BAE=∠BED，∴∠ABE+∠AEB=∠DEO+∠AEB，∴∠ABE=∠DEO，
∵∠BAE=∠EOD，∴△ABE∽△OED．
设OE=x，则AE=3eq \r(5)﹣x （0由△ABE∽△OED得，∴
∴m=eq \f(1,5)x(3eq \r(5)-x)=- eq \f(1,5)x2+eq \f(3,5)eq \r(5)x（0∴顶点为（eq \f(3,2)eq \r(5)，eq \f(9,4)）
如答图3，当m=eq \f(9,4)时，OE=x=eq \f(3,2)eq \r(5)，此时E点有1个；
当0∴当m=eq \f(9,4)时，E点只有1个
当0 在平面直角坐标系xOy中，已知两点A（0，3），B（1，0），现将线段AB绕点B按顺时针方向旋转90°得到线段BC，抛物线y=ax2+bx+c经过点C.
（1）如图1，若抛物线经过点A和D（﹣2，0）.
①求点C的坐标及该抛物线解析式；
②在抛物线上是否存在点P，使得∠POB=∠BAO，若存在，请求出所有满足条件的点P的坐标，若不存在，请说明理由；
（2）如图2，若该抛物线y=ax2+bx+c（a＜0）经过点E（2，1），点Q在抛物线上，且满足∠QOB=∠BAO，若符合条件的Q点恰好有2个，请直接写出a的取值范围.
【答案解析】解：（1）①如图2，∵A（0，3），B（1，0），∴OA=3，OB=1，
由旋转知，∠ABC=90°，AB=CB，∴∠ABO+∠CBE=90°，
过点C作CG⊥OB于G，
∴∠CBG+∠BCG=90°，
∴∠ABO=∠BCG，
∴△AOB≌△GBC，
∴CG=OB=1，BG=OA=3，
∴OG=OB+BG=4
∴C（4，1），
抛物线经过点A（0，3），和D（﹣2，0），
∴∴，∴抛物线解析式为y=﹣x2+x+3；
②由①知，△AOB≌△EBC，∴∠BAO=∠CBF，
∵∠POB=∠BAO，∴∠POB=∠CBF，
如图1，OP∥BC，∵B（1，0），C（4，1），
∴直线BC的解析式为y=x﹣，
∴直线OP的解析式为y=x，
∵抛物线解析式为y=﹣x2+x+3；
联立解得，或（舍）
∴P（，）；
在直线OP上取一点M（3，1），∴点M的对称点M'（3，﹣1），
∴直线OP'的解析式为y=﹣x，
∵抛物线解析式为y=﹣x2+x+3；
联立解得，或（舍），
∴P'（，﹣）；
（2）同（1）②的方法，如图3，
∵抛物线y=ax2+bx+c经过点C（4，1），E（2，1），
∴，∴，∴抛物线y=ax2﹣6ax+8a+1，
令y=0，∴ax2﹣6ax+8a+1=0，∴x1×x2=
∵符合条件的Q点恰好有2个，
∴方程ax2﹣6ax+8a+1=0有一个正根和一个负根或一个正根和0，
∴x1×x2=≤0，
∵a＜0，∴8a+1≥0，∴a≥﹣，
即：﹣≤a＜0.
如图1，二次函数y=ax2﹣2ax﹣3a（a＜0）的图象与x轴交于A、B两点（点A在点B的右侧），与y轴的正半轴交于点C，顶点为D.
（1）求顶点D的坐标（用含a的代数式表示）；
（2）若以AD为直径的圆经过点C.
①求抛物线的函数关系式；
②如图2，点E是y轴负半轴上一点，连接BE，将△OBE绕平面内某一点旋转180°，得到△PMN（点P、M、N分别和点O、B、E对应），并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段MF：BF=1：2，求点M、N的坐标；
③点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，如图3，求点Q的坐标.
【答案解析】解：（1）∵y=ax2﹣2ax﹣3a=a（x﹣1）2﹣4a，
∴D（1，﹣4a）.
（2）①∵以AD为直径的圆经过点C，
∴△ACD为直角三角形，且∠ACD=90°；
由y=ax2﹣2ax﹣3a=a（x﹣3）（x+1）知，
A（3，0）、B（﹣1，0）、C（0，﹣3a），则：
AC2=（0﹣3）2+（﹣3a﹣0）2=9a2+9、CD2=（0﹣1）2+（﹣3a+4a）2=a2+1、
AD2=（3﹣1）2+（0+4a）2=16a2+4
由勾股定理得：AC2+CD2=AD2，即：9a2+9+a2+1=16a2+4，
化简，得：a2=1，由a＜0，得：a=﹣1
即，抛物线的解析式：y=﹣x2+2x+3.
②∵将△OBE绕平面内某一点旋转180°得到△PMN，
∴PM∥x轴，且PM=OB=1；
设M（x，﹣x2+2x+3），则OF=x，MF=﹣x2+2x+3，BF=OF+OB=x+1；
∵MF：BF=1：2，即BF=2MF，
∴2（﹣x2+2x+3）=x+1，化简，得：2x2﹣3x﹣5=0
解得：x1=﹣1、x2=
∴M（，）、N（，）.
③设⊙Q与直线CD的切点为G，连接QG，过C作CH⊥QD于H，如右图；
设Q（1，b），则QD=4﹣b，QB2=QG2=（1+1）2+（b﹣0）2=b2+4；
∵C（0，3）、D（1，4），
∴CH=DH=1，即△CHD是等腰直角三角形，
∴△QGD也是等腰直角三角形，即：QD2=2QG2；
代入数据，得：（4﹣b）2=2（b2+4），化简，得：b2+8b﹣8=0，
解得：b=﹣4±2；
即点Q的坐标为（1，﹣4+2）或（1，﹣4﹣2）.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与x轴交于点A（-eq \f(1,2),0）,B(2,0),与y轴交于点C,以O为圆心,半径为1的☉O恰好经过点C,与x轴的正半轴交于点D.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴交x轴于点E,连接CE,并延长CE交☉O于点F,求EF的长;
(3)设点P(m,n)为☉O上的任意一点,当 SKIPIF 1 < 0 的值最大时,求此时直线BP的函数表达式.
【答案解析】解:(1)由题意知点C(0,1),将A（-eq \f(1,2),0）,B(2,0),C(0,1)分别代入得
解得∴抛物线的函数表达式为y=-x2+eq \f(3,2)x+1.
(2)抛物线的对称轴为直线x=eq \f(3,4),∴E点（eq \f(3,4)，0）,∴CE==1.25.
设☉O与y轴的负半轴交于点G,连接FG,则∠CFG=90°=∠COE.
又∵∠OCE是公共角,∴△CEO∽△CGF,∴=,∴CF=,∴EF=-=.
(3)如图,过点P作x轴的垂线,垂足为H,
则BH=2-m,PH=|n|.
在Rt△PHB中,tanB= SKIPIF 1 < 0 .
因为tanB随∠B的增大而增大,所以当 SKIPIF 1 < 0 的值最大时,
∠B的值最大,此时,直线与☉O相切,切点为点P,切线与y轴交于点M,
连接OP,在Rt△OPB中,sinB= SKIPIF 1 < 0 =eq \f(1,2),所以∠B=30°.
在Rt△OMB中,易得OM=eq \f(2\r(3),3),∴M（0，eq \f(2\r(3),3)）.
用待定系数法求得直线BP的函数表达式为y=-eq \f(\r(3),3)x+eq \f(2\r(3),3);
同理可求得当点P在x轴下方时直线BP的函数表达式为y=eq \f(\r(3),3)x-eq \f(2\r(3),3).