


专题04 立体几何 -十年高考数学(文)客观题(2012-2021)真题分项详解
展开专题04 立体几何
【2021年乙卷】安徽、河南、山西、江西、甘肃、陕西、黑龙江、吉林、宁夏、新疆、青海、内蒙古
1. 在正方体中,P为的中点,则直线与所成的角为( )
A. B. C. D.
【答案】D
【解析】
【分析】平移直线至,将直线与所成的角转化为与所成的角,解三角形即可.
【详解】
如图,连接,因为∥,
所以或其补角为直线与所成的角,
因为平面,所以,又,,
所以平面,所以,
设正方体棱长为2,则,
,所以.
故选:D
【2021年乙卷】安徽、河南、山西、江西、甘肃、陕西、黑龙江、吉林、宁夏、新疆、青海、内蒙古
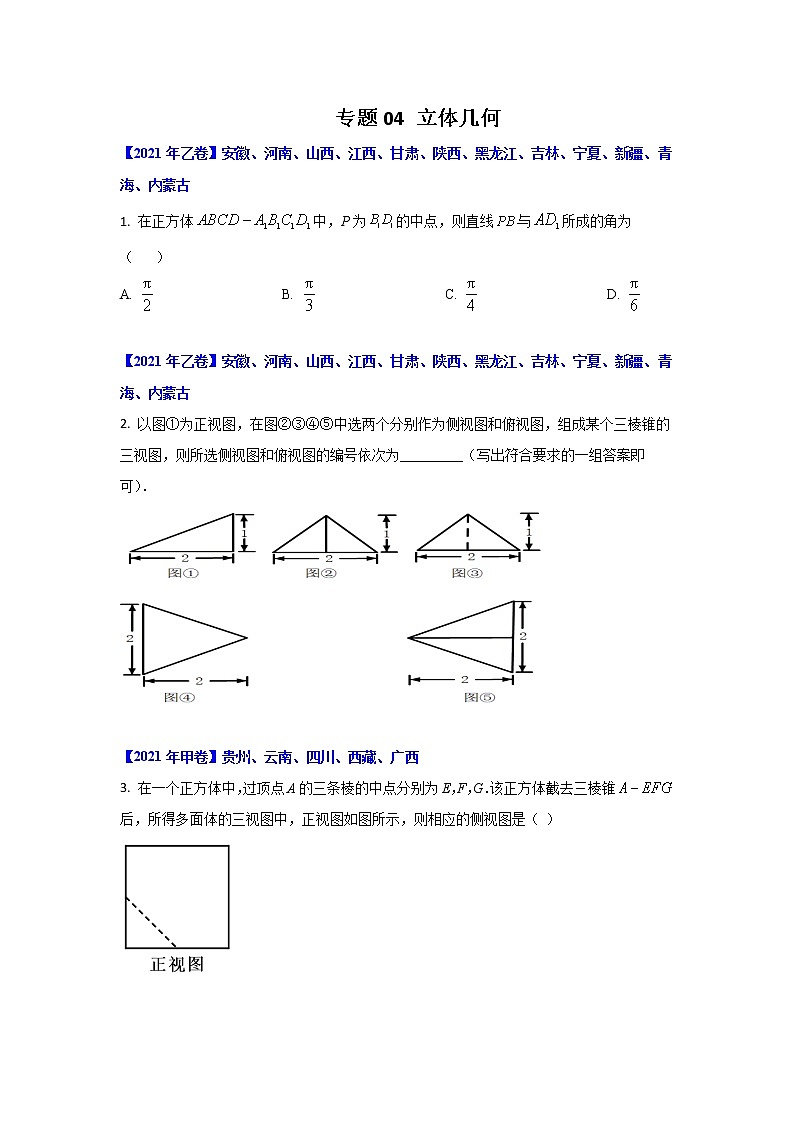
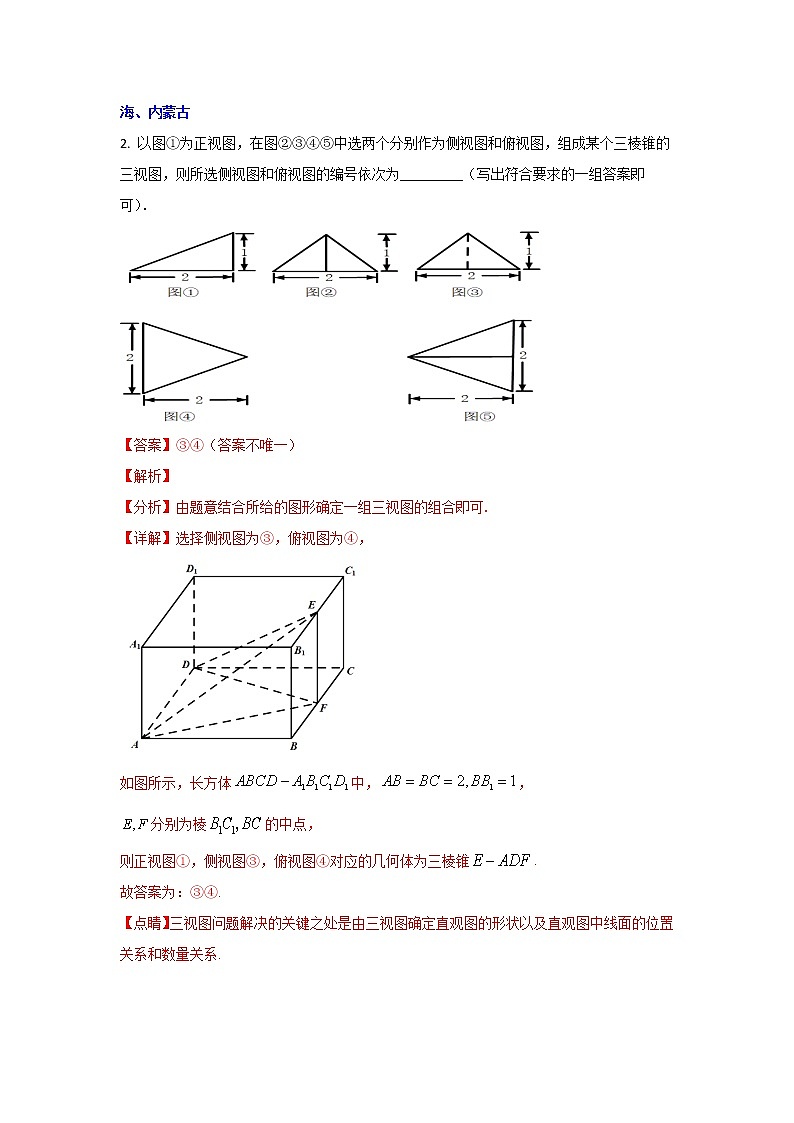
2. 以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).
【答案】③④(答案不唯一)
【解析】
【分析】由题意结合所给的图形确定一组三视图的组合即可.
【详解】选择侧视图为③,俯视图为④,
如图所示,长方体中,,
分别为棱的中点,
则正视图①,侧视图③,俯视图④对应的几何体为三棱锥.
故答案为:③④.
【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.
【2021年甲卷】贵州、云南、四川、西藏、广西
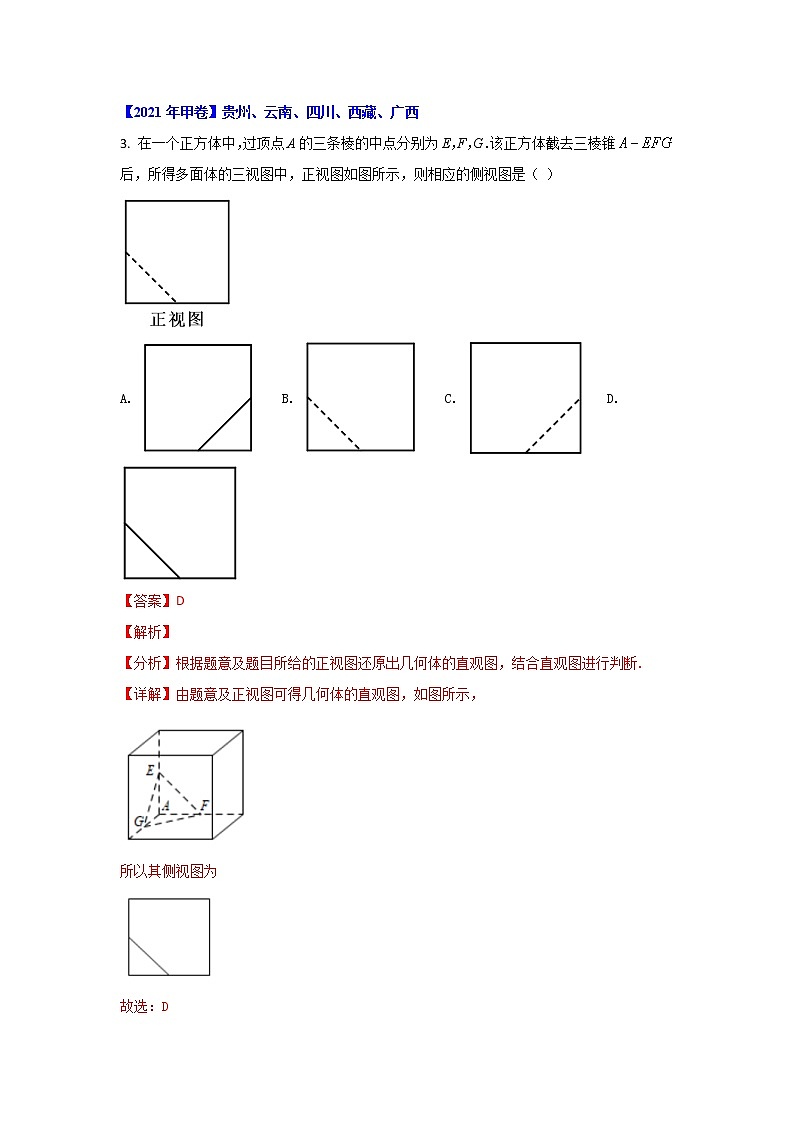
3. 在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据题意及题目所给的正视图还原出几何体的直观图,结合直观图进行判断.
【详解】由题意及正视图可得几何体的直观图,如图所示,
所以其侧视图为
故选:D
【2021年甲卷】贵州、云南、四川、西藏、广西
4. 已知一个圆锥的底面半径为6,其体积为则该圆锥的侧面积为________.
【答案】
【解析】
【分析】利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案.
【详解】∵
∴
∴
∴.
故答案为:.
【2021年新课标1卷】山东、广东、河北、江苏、湖北、湖南、福建
5. 已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为( )
A. B. C. D.
【答案】B
【解析】
【分析】设圆锥的母线长为,根据圆锥底面圆的周长等于扇形的弧长可求得的值,即为所求.
【详解】设圆锥的母线长为,由于圆锥底面圆的周长等于扇形的弧长,则,解得.
故选:B.
【2021年新课标1卷】山东、广东、河北、江苏、湖北、湖南、福建
6. 正三棱柱中,,点满足,其中,,则( )
A. 当时,的周长为定值
B. 当时,三棱锥的体积为定值
C. 当时,有且仅有一个点,使得
D. 当时,有且仅有一个点,使得平面
【答案】BD
【解析】
【分析】对于A,由于等价向量关系,联系到一个三角形内,进而确定点的坐标;
对于B,将点的运动轨迹考虑到一个三角形内,确定路线,进而考虑体积是否为定值;
对于C,考虑借助向量的平移将点轨迹确定,进而考虑建立合适的直角坐标系来求解点的个数;
对于D,考虑借助向量的平移将点轨迹确定,进而考虑建立合适的直角坐标系来求解点的个数.
【详解】
易知,点在矩形内部(含边界).
对于A,当时,,即此时线段,周长不是定值,故A错误;
对于B,当时,,故此时点轨迹为线段,而,平面,则有到平面的距离为定值,所以其体积为定值,故B正确.
对于C,当时,,取,中点分别为,,则,所以点轨迹为线段,不妨建系解决,建立空间直角坐标系如图,,,,则,,,所以或.故均满足,故C错误;
对于D,当时,,取,中点为.,所以点轨迹为线段.设,因为,所以,,所以,此时与重合,故D正确.
故选:BD.
【点睛】本题主要考查向量的等价替换,关键之处在于所求点的坐标放在三角形内.
【2020年】
7.(2020·新课标Ⅰ文)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B. C. D.
【答案】D
【解析】如图,设,则,
由题意,即,化简得,
解得(负值舍去).
8.(2020·新课标Ⅰ文)已知为球的球面上的三个点,⊙为的外接圆,若⊙的面积为,,则球的表面积为( )
A. 64π B. 48π C. 36π D. 32π
【答案】A
【解析】设圆半径为,球的半径为,依题意,
得,
由正弦定理可得,
,根据圆截面性质平面,
,
球的表面积.
9、(2020·新课标Ⅲ)下图为某几何体的三视图,则该几何体的表面积是( )
A. 6+4 B. 4+4 C. 6+2 D. 4+2
【答案】C
【解析】根据三视图特征,在正方体中截取出符合题意的立体图形
根据立体图形可得:
根据勾股定理可得:
是边长为的等边三角形
根据三角形面积公式可得:
该几何体的表面积是:.
10.(2020·北京卷)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).
A B. C. D.
【答案】D
【解析】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,
则其表面积为:.
11.(2020·山东卷)日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
A. 20° B. 40°
C. 50° D. 90°
【答案】B
【解析】画出截面图如下图所示,其中是赤道所在平面的截线;是点处的水平面的截线,依题意可知;是晷针所在直线.是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,
根据平面平行的性质定理可得可知、根据线面垂直的定义可得..
由于,所以,
由于,
所以,也即晷针与点处的水平面所成角为.
12.(2020·天津卷)若棱长为的正方体的顶点都在同一球面上,则该球的表面积为( )
A. B. C. D.
【答案】C
【解析】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,
即,
所以,这个球的表面积为.
13.(2020·浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A. B. C. 3 D. 6
【答案】A
【解析】由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,
且三棱锥的一个侧面垂直于底面,且棱锥的高为1,
棱柱的底面为等腰直角三角形,棱柱的高为2,
所以几何体的体积为:
.
14.(2020·山东卷)已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以为球心,为半径的球面与侧面BCC1B1的交线长为________.
【答案】.
【解析】如图:
取的中点为,的中点为,的中点为,
因为60°,直四棱柱的棱长均为2,所以△为等边三角形,所以,,
又四棱柱为直四棱柱,所以平面,所以,
因为,所以侧面,
设为侧面与球面的交线上的点,则,
因为球的半径为,,所以,
所以侧面与球面的交线上的点到的距离为,
因为,所以侧面与球面的交线是扇形的弧,
因为,所以,
所以根据弧长公式可得.
15.(2020·浙江卷)已知圆锥展开图的侧面积为2π,且为半圆,则底面半径为_______.
【答案】1
【解析】设圆锥底面半径为,母线长为,则
,解得.
16.(2020·江苏卷)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半轻为0.5 cm,则此六角螺帽毛坯的体积是____cm.
【答案】
【解析】正六棱柱体积为
圆柱体积为
所求几何体体积为
17.(2020·新课标Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.
【答案】
【解析】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,
其中,且点M为BC边上的中点,
设内切圆的圆心为,
由于,故,
设内切圆半径为,则:
,
解得:,其体积:.
【2019年】
18.【2019·全国Ⅱ卷文数】设α,β为两个平面,则α∥β的充要条件是
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
【答案】B
【解析】由面面平行的判定定理知:内两条相交直线都与平行是的充分条件,由面面平行性质定理知,若,则内任意一条直线都与平行,所以内两条相交直线都与平行是的必要条件,故选B.
19.【2019·全国Ⅲ卷文数】如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
【答案】B
【解析】如图所示,作于,连接,BD,易得直线BM,EN 是三角形EBD的中线,是相交直线.
过作于,连接,
平面平面,平面,平面,平面,与均为直角三角形.设正方形边长为2,易知,,,故选B.
20【2019·浙江卷】祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是
A.158 B.162
C.182 D.324
【答案】B
【解析】由三视图得该棱柱的高为6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为.
故选B.
21.【2019·浙江卷】设三棱锥V–ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点(不含端点).记直线PB与直线AC所成的角为α,直线PB与平面ABC所成的角为β,二面角P–AC–B的平面角为γ,则
A.β<γ,α<γ B.β<α,β<γ
C.β<α,γ<α D.α<β,γ<β
【答案】B
【解析】如图,为中点,连接VG,在底面的投影为,则在底面的投影在线段上,过作垂直于于E,连接PE,BD,易得,过作交于,连接BF,过作,交于,则,结合△PFB,△BDH,△PDB均为直角三角形,可得,即;在Rt△PED中,,即,综上所述,答案为B.
22.【2019·全国Ⅰ卷文数】已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为,那么P到平面ABC的距离为___________.
【答案】
【解析】作分别垂直于,平面,连接,
由题意可知,,
平面,又平面,,
,,,
,
又易知,为的平分线,
,
又,.
23.【2019·全国Ⅱ卷文数】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)
【答案】26,
【解析】由图可知第一层(包括上底面)与第三层(包括下底面)各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有个面.
如图,设该半正多面体的棱长为,则,延长与的延长线交于点,延长交正方体的棱于,由半正多面体对称性可知,为等腰直角三角形,[来源:Z|xx|k.Com]
,
,
即该半正多面体的棱长为.
24.【2019·全国Ⅲ卷文数】学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体挖去四棱锥O −EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,,3D打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为___________g.
【答案】118.8
【解析】由题意得,,
∵四棱锥O−EFGH的高为3cm, ∴.
又长方体的体积为,
所以该模型体积为,
其质量为.
25.【2019·北京卷文数】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.
【答案】40
【解析】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱之后余下的几何体,
则几何体的体积.
26.【2019·北京卷文数】已知l,m是平面外的两条不同直线.给出下列三个论断:
①l⊥m;②m∥;③l⊥.
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.
【答案】如果l⊥α,m∥α,则l⊥m.
【解析】将所给论断,分别作为条件、结论,得到如下三个命题:
(1)如果l⊥α,m∥α,则l⊥m,正确;
(2)如果l⊥α,l⊥m,则m∥α,不正确,有可能m在平面α内;
(3)如果l⊥m,m∥α,则l⊥α,不正确,有可能l与α斜交、l∥α.
故答案为:如果l⊥α,m∥α,则l⊥m.
27.【2019·天津卷文数】已知四棱锥的底面是边长为的正方形,侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________.
【答案】
【解析】由题意,四棱锥的底面是边长为的正方形,侧棱长均为,借助勾股定理,可知四棱锥的高为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,一个底面的圆心为四棱锥底面的中心,故圆柱的高为,圆柱的底面半径为,故圆柱的体积为.
28.【2019·江苏卷】如图,长方体的体积是120,E为的中点,则三棱锥E−BCD的体积是 ▲ .
【答案】10
【解析】因为长方体的体积为120,所以,
因为为的中点,所以,
由长方体的性质知底面,
所以是三棱锥的底面上的高,
所以三棱锥的体积.
【2018年】
29.【2018·全国Ⅰ卷文数】某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为
A. B.
C.3 D.2
【答案】B
【解析】根据圆柱的三视图以及其本身的特征,知点M在上底面上,点N在下底面上,且可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故选B.
30.【2018·全国Ⅲ卷文数】中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是
【答案】A
【解析】由题意知,题干中所给的是榫头,是凸出的几何体,求得是卯眼的俯视图,卯眼是凹进去的,即俯视图中应有一不可见的长方形,且俯视图应为对称图形.故选A.
31.【2018·全国I卷文数】在长方体中,,与平面所成的角为,则该长方体的体积为
A.8 B.
C. D.
【答案】C
【解析】在长方体中,连接,
根据线面角的定义可知,因为,所以,从而求得,
所以该长方体的体积为,故选C.
32.【2018·全国I卷文数】已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为
A. B.
C. D.
【答案】B
【解析】根据题意,可得截面是边长为的正方形,
结合圆柱的特征,可知该圆柱的底面为半径是的圆,且高为,
所以其表面积为,故选B.
33.【2018·浙江卷】某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是
A.2 B.4
C.6 D.8[来源:学科网ZXXK]
【答案】C
【解析】根据三视图可得几何体为一个直四棱柱,高为2,底面为直角梯形,上、下底分别为1,2,梯形的高为2,因此几何体的体积为故选C.
34.【2018·全国Ⅲ卷文数】设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为
A. B.
C. D.
【答案】B
【解析】如图所示,设点M为三角形ABC的重心,E为AC中点,
当点在平面上的射影为时,三棱锥的体积最大,此时,,
,,点M为三角形ABC的重心,,
中,有,,
,故选B.
35.【2018·全国Ⅱ卷文数】在正方体中,为棱的中点,则异面直线与所成角的正切值为
A. B.
C. D.
【答案】C
【解析】如图,在正方体中,,所以异面直线与所成角为,设正方体边长为,则由为棱的中点,可得,所以,则.故选C.
36.【2018·浙江卷】已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】A
【解析】因为,所以根据线面平行的判定定理得.由不能得出与内任一直线平行,所以是的充分不必要条件,故选A.
37.【2018·浙江卷】已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S−AB−C的平面角为θ3,则
A.θ1≤θ2≤θ3 B.θ3≤θ2≤θ1
C.θ1≤θ3≤θ2 D.θ2≤θ3≤θ1
【答案】D
【解析】设O为正方形ABCD的中心,M为AB中点,过E作BC的平行线EF,交CD于F,过O作ON垂直EF于N,连接SO,SN,SE,SM,OM,OE,则SO垂直于底面ABCD,OM垂直于AB,
因此从而
因为,所以即,故选D.
38.【2018·北京卷文数】某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为
A.1 B.2
C.3 D.4
【答案】C
【解析】由三视图可得四棱锥如图所示,
在四棱锥中,,
由勾股定理可知:,
则在四棱锥中,直角三角形有:,共3个,
故选C.
39.【2018·江苏卷】如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.
【答案】
【解析】由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于,所以该多面体的体积为.
40.【2018·天津卷文数】如图,已知正方体ABCD–A1B1C1D1的棱长为1,则四棱锥A1–BB1D1D的体积为__________.
【答案】
【解析】如图所示,连接,交于点,很明显在平面上的射影是点O,则是四棱锥A1–BB1D1D的高,且,,
结合四棱锥体积公式可得其体积为:.
41.【2018·全国II卷文数】已知圆锥的顶点为,母线,互相垂直,与圆锥底面所成角为,若的面积为,则该圆锥的体积为__________.
【答案】8π
【解析】如下图所示,,又,解得,所以,所以该圆锥的体积为.
【2017年】[来源:Z&xx&k.Com]
42.【2017·全国Ⅰ卷文数】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是
A. B.
C. D.
【答案】A
【解析】对于B,易知AB∥MQ,则直线AB∥平面MNQ;对于C,易知AB∥MQ,则直线AB∥平面MNQ;对于D,易知AB∥NQ,则直线AB∥平面MNQ.故排除B,C,D,选A.
43.【2017·全国Ⅱ卷文数】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为
A. B.
C. D.
【答案】B
【解析】由题意,该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱,故其体积为,故选B.[来源:学§科§网]
44.【2017·全国Ⅲ卷文数】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为
A. B.
C. D.
【答案】B
【解析】绘制圆柱的轴截面如图所示,由题意可得:,结合勾股定理,底面半径,由圆柱的体积公式,可得圆柱的体积是,故选B.
45.【2017·全国Ⅲ卷文数】在正方体中,E为棱CD的中点,则
A. B.
C. D.
【答案】C
【解析】根据三垂线定理的逆定理,可知平面内的线垂直于平面的斜线,则也垂直于斜线在平面内的射影.A.若,那么,很显然不成立;B.若,那么,显然不成立;
C.若,那么,成立,反过来时,也能推出,所以C成立;
D.若,则,显然不成立,故选C.
46.【2017·北京卷文数】某三棱锥的三视图如图所示,则该三棱锥的体积为
A.60 B.30
C.20 D.10
【答案】D
【解析】该几何体是如下图所示的三棱锥.
由图中数据可得该几何体的体积是,故选D.
47.【2017·浙江卷】某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是
A. B.
C. D.
【答案】A
【解析】根据所给三视图可还原几何体为半个圆锥和半个棱锥拼接而成的组合体,所以,几何体的体积为,故选A.
48.【2017·浙江卷】如图,已知正四面体(所有棱长均相等的三棱锥),P,Q,R分别为AB,BC,CA上的点,AP=PB,,分别记二面角D–PR–Q,D–PQ–R,D–QR–P的平面角为,则
A. B.
C. D.
【答案】B
【解析】设O为三角形ABC中心,则O到PQ距离最小,O到PR距离最大,O到RQ距离居中,而三棱锥的高相等,因此,所以选B.
49.【2017·全国Ⅰ卷文数】已知三棱锥S−ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S−ABC的体积为9,则球O的表面积为________.
【答案】
【解析】取的中点,连接,
因为,所以,
因为平面平面,所以平面,
设,则,
所以,所以球的表面积为.
50.【2017·全国Ⅱ卷文数】长方体的长,宽,高分别为,其顶点都在球的球面上,则球的表面积为 .
【答案】
【解析】球的直径是长方体的体对角线,所以
51.【2017·天津卷文数】已知一个正方形的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为___________.
【答案】
【解析】设正方体的边长为,则,其外接球直径为,故这个球的体积.
52.【2017·山东卷文数】由一个长方体和两个圆柱体构成的几何体的三视图如图,则该几何体的体积为 .
【答案】
【解析】由三视图可知,长方体的长、宽、高分别为2,1,1,圆柱的高为1,底面圆的半径为1,所以
.
53.【2017·江苏卷】如图,在圆柱内有一个球,该球与圆柱的上、下底面及母线均相切.记圆柱的体积为,球的体积为,则的值是 .
【答案】
【解析】设球半径为,则.故答案为.
【2016年】
54.【2016·新课标1文数】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是,则它的表面积是( )
(A)17π (B)18π (C)20π (D)28π
【答案】A[
【解析】由三视图知,该几何体的直观图如图所示:
是一个球被切掉左上角的,即该几何体是个球,设球的半径为,则,解得,所以它的表面积是的球面面积和三个扇形面积之和,即,故选A.
55.【2016·新课标1文数】平面过正文体ABCD—A1B1C1D1的顶点A,,,则m,n所成角的正弦值为( )
(A) (B) (C) (D)
【答案】A
【解析】如图,设平面平面=,平面平面=,因为平面,所以,则所成的角等于所成的角.延长,过作,连接,则为,同理为,而,则所成的角即为所成的角,即为,故所成角的正弦值为,选A.
56.【2016·上海文科】如图,在正方体ABCD−A1B1C1D1中,E、F分别为BC、BB1的中点,则下列直线中与直线EF相交的是( )
(A)直线AA1 (B)直线A1B1
(C)直线A1D1 (D)直线B1C1
【答案】D
【解析】只有与在同一平面内,是相交的,其他A,B,C中的直线与都是异面直线,故选D.
57.【2016·浙江文数】已知互相垂直的平面交于直线l.若直线m,n满足m∥α,n⊥β,则( )
A.m∥l B.m∥n C.n⊥l D.m⊥n
【答案】C
【解析】由题意知,.故选C.
58.【2016·天津文数】将一个长方形沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图所示,则该几何体的侧(左)视图为( )
【答案】B
【解析】由题意得截去的是长方体前右上方的顶点,故选B.
59. [2016·新课标Ⅲ文数]如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为( )
(A) (B) (C)90 (D)81
【答案】B
【解析】由三视图该几何体是以侧视图为底面的斜四棱柱,所以该几何体的表面积
,故选B.
60.【2016·山东文数】一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )[来源:学科网ZXXK]
(A)(B)
(C)(D)
【答案】C
【解析】由已知,半球的直径为,正四棱锥的底面边长为1,高为1,所以其体积为,选C.
61.【2016·山东文数】已知直线a,b分别在两个不同的平面α,内,则“直线a和直线b相交”是“平面α和平面相交”的( )
(A)充分不必要条件(B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
【答案】A
【解析】 “直线和直线相交”“平面和平面相交”,但“平面和平面相交”“直线和直线相交”,所以“直线和直线相交”是“平面和平面相交”的充分不必要条件,故选A.
62. [2016·新课标Ⅲ文数]在封闭的直三棱柱内有一个体积为的球,若,
,,,则的最大值是( )
(A)4π (B) (C)6π (D)
【答案】B
【解析】要使球的体积最大,必须球的半径最大.由题意知球的与直三棱柱的上下底面都相切时,
球的半径取得最大值,此时球的体积为,故选B.
63.【2016·浙江文数】某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.
【答案】80;40.
【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体, ,.
64.【2016·浙江文数】如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=,∠ADC=90°.沿直线AC将△ACD翻折成△,直线AC与所成角的余弦的最大值是______.
【答案】
【解析】如图,连接BD′,设直线与所成的角为.
是的中点.由已知得,以为轴,为轴,过与平面垂直的直线为轴,建立空间直角坐标系,则,,.作于,连接D′H翻折过程中,始终与垂直, 则,则,,因此(设∠DHD′=α),
则,与平行的单位向量为,
所以=,所以时,取得最大值,为.
65.【2016·四川文科】已知某三菱锥的三视图如图所示,则该三棱锥的体积 .
【答案】
【解析】由三视图可知该几何体是一个三棱锥,且底面积为,高为1,所以该三棱锥的体积为
66.【2016·北京文数】某四棱柱的三视图如图所示,则该四棱柱的体积为___________.
【答案】
【解析】四棱柱高为1,底面为等腰梯形,面积为,因此体积为
67.(2015新课标I文)《九章算术》是我国古代内容极为丰富的数学明著,书中有如下问题:”今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?“其意思为:”在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?“已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
A.
14斛
B.
22斛
C.
36斛
D.
66斛
解:设圆锥的底面半径为r,则×2×3r=8,解得r=,
故米堆的体积为××3×()2×5=,∵1斛米的体积约为1.62立方,
∴÷1.62≈22,故选:B.
68.(2015新课标I文)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )
A.
1
B.
2
C.
4
D.
8
解:由几何体三视图中的正视图和俯视图可知,
截圆柱的平面过圆柱的轴线,
该几何体是一个半球拼接半个圆柱,
∴其表面积为:×4πr2+×πr22r×2πr+2r×2r+×πr2=5πr2+4r2,
又∵该几何体的表面积为16+20π,
∴5πr2+4r2=16+20π,解得r=2,
故选:B.
【2015新课标2卷文】
69.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为
A. B. C. D.
解析:还原三视图,如图所示,选D.
【2015新课标2卷文】
70.已知A,B是球O的球面上两点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为
A. 36π B. 64π C. 144π D.256π
解析:因为A,B都在球面上,又所以
三棱锥的体积的最大值为,所以R=6,所以球的表面积为S=π,故选C.
【2014新课标1卷文】
71.如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
【答案】:B
【解析】:根据所给三视图易知,对应的几何体是一个横放着的三棱柱. 选B
【2014新课标2卷文】
72.如图,网格纸上正方形小格的边长为1(表示1cm),
图中粗线画出的是某零件的三视图,该零件
由一个底面半径为3cm,高为6c m的圆柱
体毛坯切削得到,则切削掉部分的体积与
原来毛坯体积的比值为
(A) (B) (C) (D)
【答案】 C
【解析】
【2014新课标2卷文】
73.正三棱柱的底面边长为2,侧棱长为,D为BC中点,则三棱锥的体积为
(A)3 (B) (C)1 (D)
【答案】 C
【解析】
【2013新课标卷】
74.某几何体的三视图如图所示,则该几何体的体积为( ).
A.16+8π
B.8+8π
C.16+16π
D.8+16π
答案:A
解析:该几何体为一个半圆柱与一个长方体组成的一个组合体.
V半圆柱=π×22×4=8π,
V长方体=4×2×2=16.
所以所求体积为16+8π.故选A.
【2013新课标卷】
75.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为______.
答案:
解析:如图,
设球O的半径为R,
则AH=,
OH=.
又∵π·EH2=π,∴EH=1.
∵在Rt△OEH中,R2=,∴R2=.
∴S球=4πR2=.
【2012新课标卷】
76.若一个几何体的三视图如右图所示,则此几何体的体积为
(A) (B) (C) (D)
【考点定位】本题是基础题,考查三视图与直观图的关系,注意几何体的位置与放法是解题的关键,考查空间想象能力,转化思想、计算能力.
专题03 导数及其应用 -十年高考数学(文)客观题(2012-2021)真题分项详解: 这是一份专题03 导数及其应用 -十年高考数学(文)客观题(2012-2021)真题分项详解,文件包含专题03导数及其应用解析版-十年高考数学文客观题2012-2021真题分项详解doc、专题03导数及其应用原卷版-十年高考数学文客观题2012-2021真题分项详解doc等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
专题02 函数性质及其应用-十年高考数学(文)客观题(2012-2021)真题分项详解: 这是一份专题02 函数性质及其应用-十年高考数学(文)客观题(2012-2021)真题分项详解,文件包含专题02函数性质及其应用解析版-十年高考数学文客观题2012-2021真题分项详解doc、专题02函数性质及其应用原卷版-十年高考数学文客观题2012-2021真题分项详解doc等2份试卷配套教学资源,其中试卷共80页, 欢迎下载使用。
专题10 概率与统计 -十年高考数学(文)客观题(2012-2021)真题分项详解: 这是一份专题10 概率与统计 -十年高考数学(文)客观题(2012-2021)真题分项详解,文件包含专题10概率与统计解析版-十年高考数学文客观题2012-2021真题分项详解doc、专题10概率与统计原卷版-十年高考数学文客观题2012-2021真题分项详解doc等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。












