初中数学2.3 三角形的内切圆课后练习题

这是一份初中数学2.3 三角形的内切圆课后练习题，文件包含浙教版数学九年级下册23三角形的内切圆练习试题解析版docx、浙教版数学九年级下册23三角形的内切圆练习试题原卷版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。

2.3三角形的内切圆
班级： 姓名：
一、单选题
1．四边形 ABCD 内接于⊙ O ，点I是 ΔABC 的内心， ∠AIC=124∘ ，点E在 AD 的延长线上，则 ∠CDE 的度数为( )
A．56°B．62°C．68°D．48°
2．如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，O是△ABC的内心，以O为圆心，r为半径的圆与线段AB有交点，则r的取值范围是（ ）
A．r≥1B．1≤r≤ 5C．1≤r≤ 10D．1≤r≤4
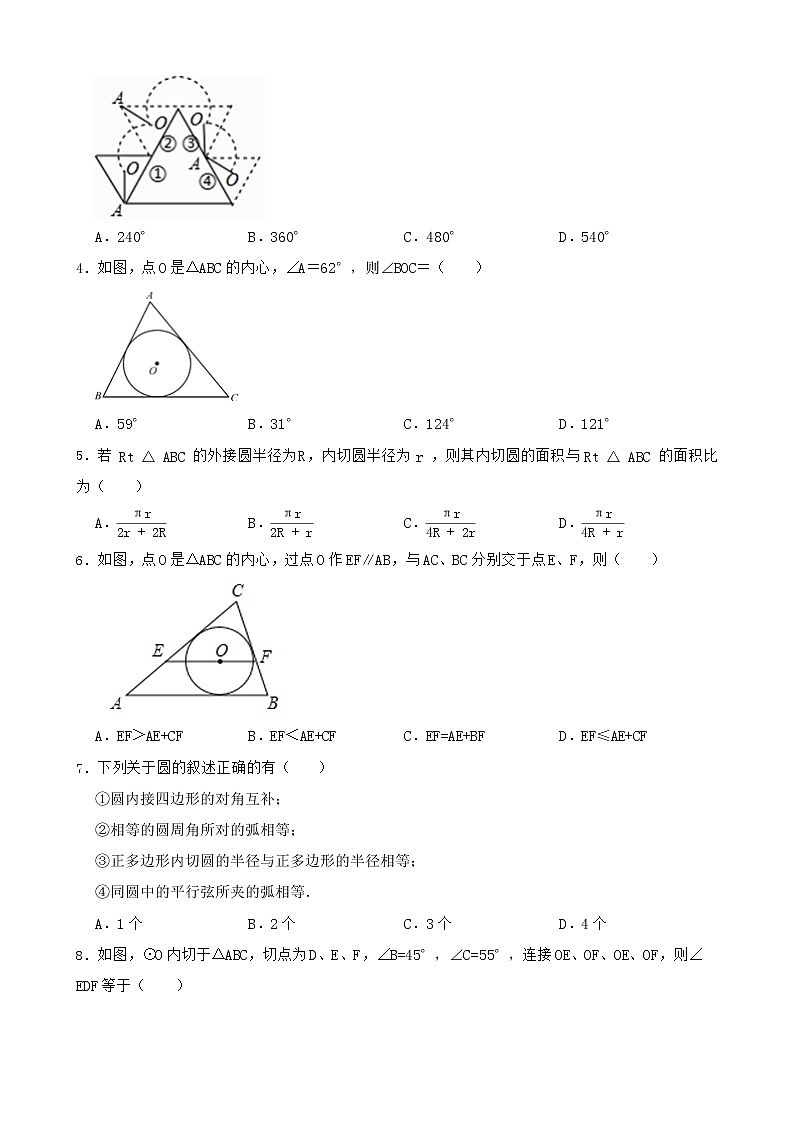
3．如图，大小不同的两个磁块，其截面都是等边三角形，小三角形边长是大三角形边长的一半，点O是小三角形的内心，现将小三角形沿着大三角形的边缘顺时针滚动，当由①位置滚动到④位置时，线段OA绕点O顺时针转过的角度是（ ）
A．240°B．360°C．480°D．540°
4．如图，点O是△ABC的内心，∠A＝62°，则∠BOC＝（ ）
A．59°B．31°C．124°D．121°
5．若 Rt△ABC 的外接圆半径为R，内切圆半径为 r ，则其内切圆的面积与 Rt△ABC 的面积比为（ ）
A．πr2r+2RB．πr2R+rC．πr4R+2rD．πr4R+r
6．如图，点O是△ABC的内心，过点O作EF∥AB，与AC、BC分别交于点E、F，则（ ）
A．EF＞AE+CFB．EF＜AE+CF C．EF=AE+BFD．EF≤AE+CF
7．下列关于圆的叙述正确的有（ ）
①圆内接四边形的对角互补；
②相等的圆周角所对的弧相等；
③正多边形内切圆的半径与正多边形的半径相等；
④同圆中的平行弦所夹的弧相等．
A．1个B．2个C．3个D．4个
8．如图，⊙O内切于△ABC，切点为D、E、F，∠B=45°，∠C=55°，连接OE、OF、OE、OF，则∠EDF等于（ ）
A．45° B．55°C．50°D．70°
9．如图，已知正△ABC的边长为6，⊙O是它的内切园，则图中阴影部分的面积为（ ）
A．3 ﹣πB．2π﹣2
C．3 ﹣ D．4 ﹣2π
二、填空题
10．如图，在扇形CAB中，CD⊥AB，垂足为D，⊙E是△ACD的内切圆，连接AE，BE，则∠AEB的度数为 ．
11．如图，在 △ABC 中，点O是 △ABC 的内心， ∠A=48° ， ∠BOC= ° ．
12．如图，在△ABC中，∠ACB=90°，BE平分∠ABC，CF平分∠ACB，CF，BE交于点P，AC=4cm，BC=3cm，AB=5cm，则△CPB的面积为 cm2．
13．如图，在平面直角坐标系中，矩形 OACB 的顶点 C(6,8) ，点 I 是 △ABC 的内心，将 △ABC 绕原点顺时针旋转 90° 后， I 的对应点 I′ 的坐标是 ．
14．如图，在Rt△ABC中，∠C=90°，∠B=60°，内切圆O与边AB、BC、CA分别相切于点D、E、F，则∠DEF的度数为 °．
15．小红随机地在如图所示的边长为6的正三角形及其内部区域投针，则针扎到其内切圆 ( 阴影 ) 区域的概率为 .
16．在△ABC中，点I是内心，若∠A=80°，则∠DEF= 度．
三、解答题
17．已知：如图，点N为△ABC的内心，延长AN交BC于点D，交△ABC的外接圆于点E．
（1）求证：EB=EN=EC；
（2）求证：NE2=AE•DE．
18．如图，∠C=90°，⊙O是Rt△ABC的内切圆，分别切BC，AC，AB于点E，F，G，连接OE，OF．AO的延长线交BC于点D，AC=6，CD=2．
（1）求证：四边形OECF为正方形；
（2）求⊙O的半径；
（3）求AB的长．
19．已知：如图，在直角坐标系中，⊙O1经过坐标原点，分别与x轴正半轴、y轴正半轴交于点A（3，0）、B（0，4）．设△BOA的内切圆的直径为d，求d+AB的值．
20．如图，在Rt△ABC中，∠C=90°，⊙O是△ABC的内切圆，切点D、E、F，
（1）求证：四边形OECF是正方形；
（2）若AF=10，BE=3，求⊙O的面积．