初中数学人教版八年级下册18.2.3 正方形优质课课件ppt

这是一份初中数学人教版八年级下册18.2.3 正方形优质课课件ppt，文件包含《1823正方形》同步精品课件pptx、《1823正方形》同步精品教案doc等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

1．掌握正方形的概念、性质和判定，并会用它们进行有关的论证和计算．（重点）2．理解正方形与平行四边形、矩形、菱形的联系和区别，进一步体会特殊与一般的关系．（难点）
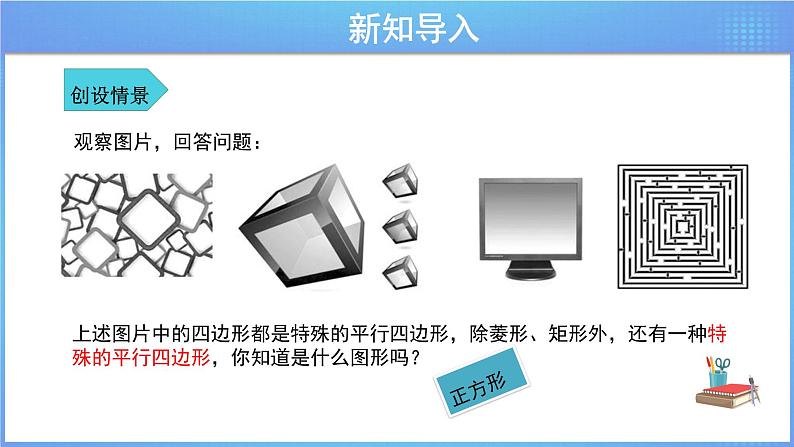
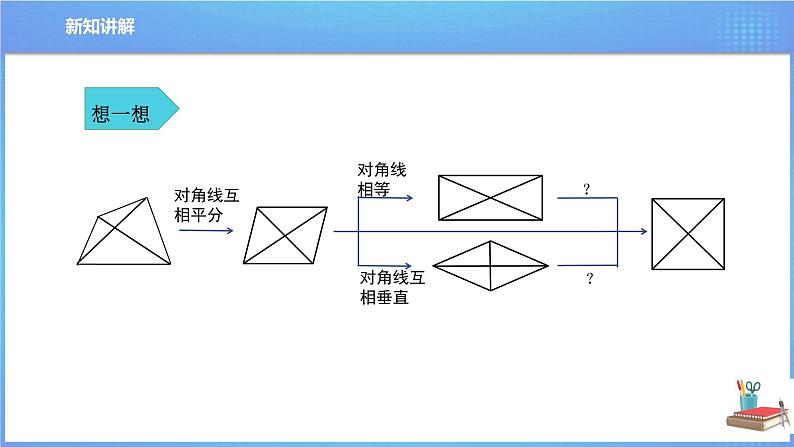
上述图片中的四边形都是特殊的平行四边形，除菱形、矩形外，还有一种特殊的平行四边形，你知道是什么图形吗？
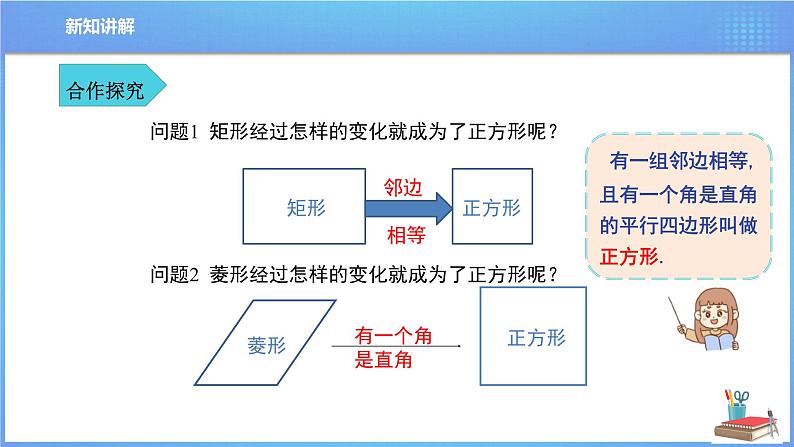
问题1 矩形经过怎样的变化就成为了正方形呢？问题2 菱形经过怎样的变化就成为了正方形呢？
有一组邻边相等,且有一个角是直角的平行四边形叫做正方形.
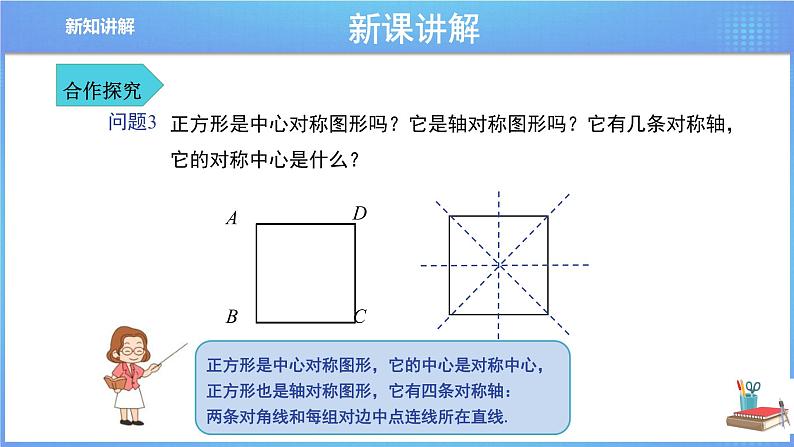
正方形是中心对称图形，它的中心是对称中心，正方形也是轴对称图形，它有四条对称轴：两条对角线和每组对边中点连线所在直线.
正方形既是矩形,又是菱形,它具有平行四边形、矩形和菱形的一切性质.正方形的性质1:正方形的四个角都是直角,四条边都相等.正方形的性质2:正方形的对角线相等且互相垂直平分.正方形的性质3:既是中心对称图形也是轴对称图形.
我们之前是怎样判定矩形和菱形的？
对于正方形我们依然从定义、边、角、对角线方面来考虑.
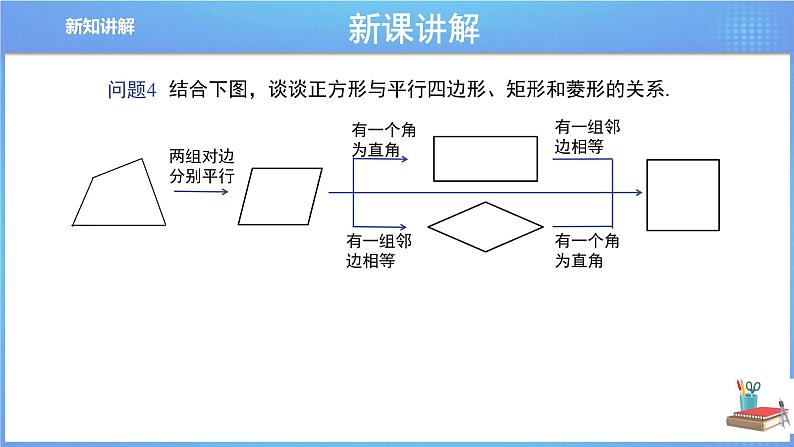
有一组邻边相等,且有一个角是直角的平行四边形
对角线相等且互相垂直平分的四边形
对角线相等且互相垂直的平行四边形
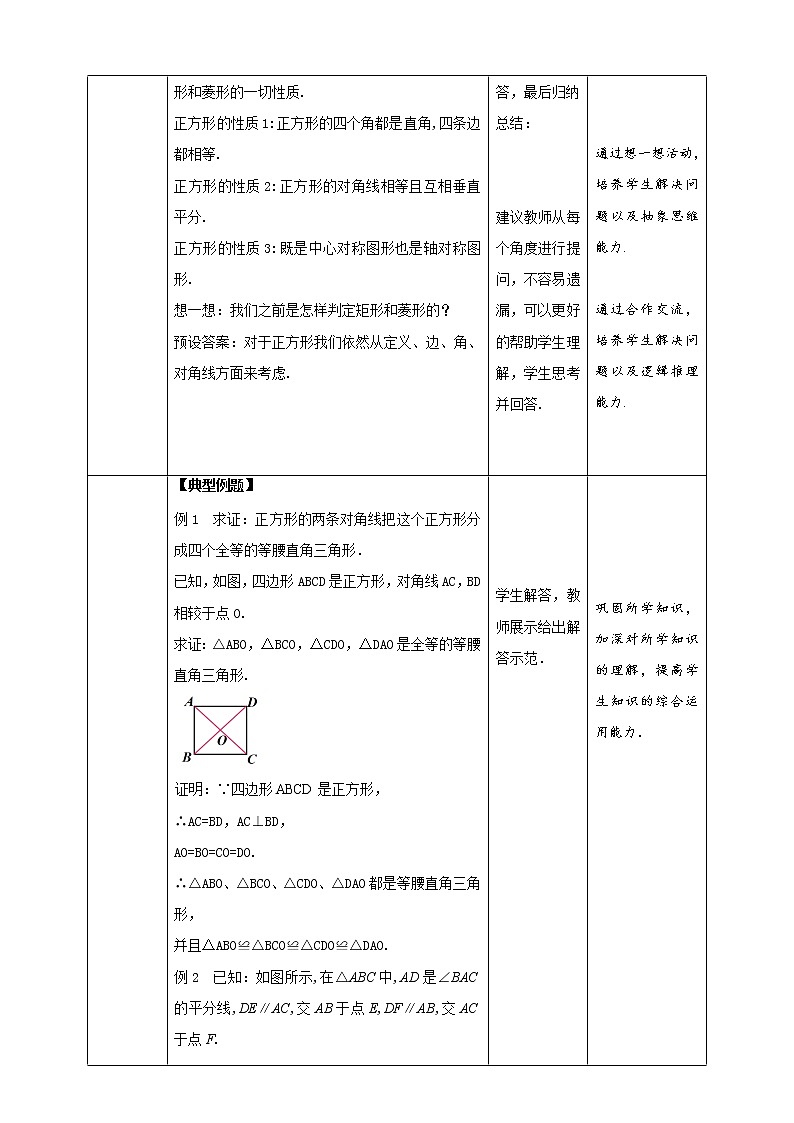
例1 求证：正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
已知，如图，四边形ABCD是正方形，对角线AC，BD相较于点O.求证：△ABO，△BCO，△CDO，△DAO是全等的等腰直角三角形.
证明：∵四边形ABCD是正方形，
∴AC=BD，AC⊥BD，
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形，并且△ABO≌△BCO≌△CDO≌△DAO.
证明:∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形.∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.∴AE=DE.∴四边形AEDF是菱形.
例2 已知：如图所示,在△ABC中,AD是∠BAC的平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点F.求证：四边形AEDF是菱形.
1.如图，在▱ABCD中，对角线AC，BD相交于点O，添加下列条件不能判定▱ABCD是菱形的只有(　　)A．AC⊥BD B．AB＝BC C．AC＝BD D．∠1＝∠2
2.如图所示,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,两弧相交于点C,D,则直线CD即为所求.连接AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是(　　)A.矩形 B.菱形C.正方形 D.等腰梯形
3.如图，四边形ABCD是正方形，延长BC到E，使CE=AC，连接AE，交CD于F，求∠AFC的度数.
解：∵四边形ABCD是正方形，∴AC平分∠BCD， ∠BCD= ∠DCE=90°.∴ ∠ACB=45°.∵CE=AC， ∠CAE+ ∠E= ∠ACB，
∴ ∠E=22.5°，∴ ∠AFC= ∠DCE+ ∠E=90°+22.5°=112.5°.
4.如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．(1)求证：AF=DC；(2)若AB⊥AC，试判断四边形ADCF的形状，说明理由．
(1)证明：∵AF∥BC，∴∠AFE=∠DBE，∠FAE=∠BDE,∵E是AD的中点，∴AE=DE，∴△AFE≌△DBE.∵AD是BC边上的中线，∴BD=CD，∴AF=BD，∴AF=DC．(2)解：四边形ADCF是菱形，理由如下： 由(1)知AF∥BC，AF=DC，∴四边形ADCF是平行四边形，∵AC⊥AB，AD是斜边BC的中线，∴AD= BC=DC，∴平行四边形ADCF是菱形．
有一组邻边相等且有一个角是直角的平行四边形是正方形.
四个角都是直角，四条边都相等两条对角线相等且互相垂直平分，既是轴对称图形，又是中心对称图形。
一个角是直角且一组邻边相等
（1）定义：有一组邻边相等且有一个角是直角的 平行四边形是正方形.
（2）性质 （3）判定
2.正方形与平行四边形、矩形和菱形的关系
教科书第59页练习 第1、2题